Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-24T14:50:54.346Z Has data issue: false hasContentIssue false
  • English
  • Français

Lp-Boundedness of a Singular Integral Operator

Published online by Cambridge University Press:  20 November 2018

Abdelnaser J. Al-Hasan  and
Dashan Fan
Abdelnaser J. Al-Hasan
Affiliation:
Department of Mathematical Sciences University of Wisconsin-Milwaukee Milwaukee, WI 53201 USA, email: naser@csd4.csd.uwm.edu
Dashan Fan
Affiliation:
Department of Mathematical Sciences University of Wisconsin-Milwaukee Milwaukee, WI 53201 USA, email: Fan@csd4.csd.uwm.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 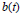$b(t)$ be an 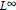${{L}^{\infty }}$ function on 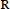$\mathbf{R}$, $\Omega ({y}')$ be an 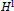${{H}^{1}}$ function on the unit sphere satisfying the mean zero property (1) and ${{Q}_{m}}(t)$ be a real polynomial on 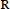$\mathbf{R}$ of degree 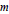$m$ satisfying ${{Q}_{m}}(0)\,=\,0$. We prove that the singular integral operator

$${{T}_{Qm,}}b\left( f \right)\left( x \right)=p.v.\int\limits_{\mathbf{R}}^{n}{b\left( \left| y \right| \right)}\Omega \left( y \right){{\left| y \right|}^{-n}}f\left( x-{{Q}_{m}}\left( \left| y \right| \right){y}' \right)\,\,dy$$

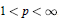is bounded in ${{L}^{p}}({{\mathbf{R}}^{n}})$ for $1<p<\infty $, and the bound is independent of the coefficients of ${{Q}_{m}}(t)$.

Keywords

42B20singular integralrough kernelHardy space
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 4 , 01 December 1998 , pp. 404 - 412
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Colzani, L., Hardy Spaces on Sphere. Ph.D. Thesis, Washington University, St. Louis, 1982.Google Scholar
2. Colzani, L., Taibleson, M. and Weiss, G., Maximal estimates for Cesàro and Riesz means on sphere. Indiana Univ. Math. J. (6) 33 (1984), 873–889.Google Scholar
3. Fan, D., Guo, K. and Pan, Y., Singular Integral along Submanifolds of Finite Type. Michigan Math. J. 45 (1998), 135–142.Google Scholar
4. Fan, D. and Pan, Y., Singular Integral Operators with Rough Kernels Supported by Subvarieties. Amer. J. Math. 119 (1997), 799–839.Google Scholar
5. Fan, D. and Pan, Y., L2-Boundedness of a singular integral operator. Publ. Mat. 41 (1997), 317–333.Google Scholar
6. Fan, D. and Pan, Y., A singular integral operator with rough kernel. Proc.Amer.Math. Soc. 125 (1997), 3695–3703.Google Scholar
7. Ricci, F. and Stein, E. M., Harmonic analysis on nilpotent groups and singular integrals I: Oscillatory integrals. J. Funct.Anal. 73 (1987), 56–84.Google Scholar
8. Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality and Oscillatory Integrals. Princeton University Press, Princeton, NJ, 1993.Google Scholar