Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hell, P.
1972.
Full embeddings into some categories of graphs.
Algebra Universalis,
Vol. 2,
Issue. 1,
p.
129.
Ne?et?il, Jaroslav
1972.
On symmetric and antisymmetric relations.
Monatshefte f�r Mathematik,
Vol. 76,
Issue. 4,
p.
323.
1973.
Graphs and Hypergraphs.
Vol. 6,
Issue. ,
p.
498.
Hell, Pavol
1974.
On some strongly rigid families of graphs and the full embeddings they induce.
Algebra Universalis,
Vol. 4,
Issue. 1,
p.
108.
Kučera, Luděk
1975.
On universal concrete categories.
Algebra Universalis,
Vol. 5,
Issue. 1,
p.
149.
Fried, E.
and
Wiegandt, R.
1975.
Connectednesses and disconnectednesses of graphs.
Algebra Universalis,
Vol. 5,
Issue. 1,
p.
411.
Babai, L.
1977.
Asymmetric trees with two prescribed degrees.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 29,
Issue. 1-2,
p.
193.
Hell, P.
and
Ne?et?il, J.
1978.
Homomorphisms of graphs and of their orientations.
Monatshefte f�r Mathematik,
Vol. 85,
Issue. 1,
p.
39.
Nešetřil, Jaroslav
and
Pultr, Aleš
1978.
On classes of relations and graphs determined by subobjects and factorobjects.
Discrete Mathematics,
Vol. 22,
Issue. 3,
p.
287.
Hell, Pavol
and
Nešetřil, Jaroslav
1979.
Cohomomorphisms of graphs and hypergraphs.
Mathematische Nachrichten,
Vol. 87,
Issue. 1,
p.
53.
Nešetřil, J.
1979.
AMALGAMATION OF GRAPHS AND ITS APPLICATIONS.
Annals of the New York Academy of Sciences,
Vol. 319,
Issue. 1,
p.
415.
Hell, Pavol
1979.
AN INTRODUCTION TO THE CATEGORY OF GRAPHS*.
Annals of the New York Academy of Sciences,
Vol. 328,
Issue. 1,
p.
120.
Babai, László
and
Pultr, Aleš
1980.
Endomorphism monoids and topological subgraphs of graphs.
Journal of Combinatorial Theory, Series B,
Vol. 28,
Issue. 3,
p.
278.
1980.
Combinatorial, Algebraic and Topological Representations of Groups, Semigroups and Categories.
Vol. 22,
Issue. ,
p.
353.
D�rfler, W.
and
Waller, D. A.
1980.
A category-theoretical approach to hypergraphs.
Archiv der Mathematik,
Vol. 34,
Issue. 1,
p.
185.
Babai, László
and
Nešetřil, Jaroslav
1982.
Algebraic and Geometric Combinatorics.
Vol. 65,
Issue. ,
p.
55.
Koubek, Václav
and
Rödl, Vojtěch
1984.
On the minimum order of graphs with given semigroup.
Journal of Combinatorial Theory, Series B,
Vol. 36,
Issue. 2,
p.
135.
Koubek, V.
and
Sichler, J.
1985.
Quotients of rigid (0,1)-lattices.
Archiv der Mathematik,
Vol. 44,
Issue. 5,
p.
403.
Zemlyachenko, V. N.
Korneenko, N. M.
and
Tyshkevich, R. I.
1985.
Graph isomorphism problem.
Journal of Soviet Mathematics,
Vol. 29,
Issue. 4,
p.
1426.
Goralčík, Pavel
and
Koubek, Václav
1986.
Verifying nonrigidity.
Information Processing Letters,
Vol. 22,
Issue. 2,
p.
91.
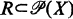 . This interpretation is generalized in the notion of society.
. This interpretation is generalized in the notion of society.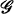 is a couple (X, R), where
is a couple (X, R), where 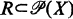 ; a k-society is a society (X, R) with |A| = k for each A ∊ R.
; a k-society is a society (X, R) with |A| = k for each A ∊ R.



