Article contents
Generalized D-symmetric Operators II
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 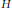 $H$ be a separable, infinite-dimensional, complex Hilbert space and let
$H$ be a separable, infinite-dimensional, complex Hilbert space and let 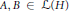 $A,\,B\,\in \,\mathcal{L}\left( H \right)$, where
$A,\,B\,\in \,\mathcal{L}\left( H \right)$, where 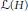 $\mathcal{L}(H)$ is the algebra of all bounded linear operators on
$\mathcal{L}(H)$ is the algebra of all bounded linear operators on 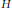 $H$. Let
$H$. Let 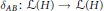 ${{\delta }_{AB}}\,:\mathcal{L}\left( H \right)\to \mathcal{L}\left( H \right)$ denote the generalized derivation
${{\delta }_{AB}}\,:\mathcal{L}\left( H \right)\to \mathcal{L}\left( H \right)$ denote the generalized derivation 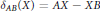 ${{\delta }_{AB}}\left( X \right)\,=\,AX\,-\,XB$. This note will initiate a study on the class of pairs
${{\delta }_{AB}}\left( X \right)\,=\,AX\,-\,XB$. This note will initiate a study on the class of pairs 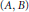 $\left( A,\,B \right)$ such that
$\left( A,\,B \right)$ such that 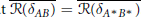 $\overline{R\left( {{\delta }_{AB}} \right)}\,=\,\overline{R\left( {{\delta }_{A*\,B*}} \right)}$.
$\overline{R\left( {{\delta }_{AB}} \right)}\,=\,\overline{R\left( {{\delta }_{A*\,B*}} \right)}$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
- 3
- Cited by


