Hostname: page-component-77c89778f8-gvh9x Total loading time: 0 Render date: 2024-07-19T18:09:23.697Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenfunction Decay For the Neumann Laplacian on Horn-Like Domains

Published online by Cambridge University Press:  20 November 2018

Julian Edward
Julian Edward*
Affiliation:
Department of Mathematics Florida International University Miami, Florida 33199 U.S.A., e-mail: edwardj@fiu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The growth properties at infinity for eigenfunctions corresponding to embedded eigenvalues of the Neumann Laplacian on horn-like domains are studied. For domains that pinch at polynomial rate, it is shown that the eigenfunctions vanish at infinity faster than the reciprocal of any polynomial. For a class of domains that pinch at an exponential rate, weaker, 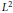${{L}^{2}}$ bounds are proven. A corollary is that eigenvalues can accumulate only at zero or infinity.

Keywords

35P2558G25Neumann Laplacianhorn-like domainspectrum
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 1 , 01 March 2000 , pp. 51 - 59
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Banuelos, R., Sharp estimates for Dirichlet eigenfunctions in simply connected domains. J. Differential Equations 125 (1996), 282–298.Google Scholar
[2] Banuelos, R. and Davis, B., Sharp estimates for Dirichlet eigenfunctions in horn-shaped regions. Comm.Math. Phys. 150 (1992), 209–215.Google Scholar
[3] Banuelos, R. and Davis, B., Correction to Sharp estimates for Dirichlet eigenfunctions in horn-shaped regions. Comm. Math. Phys. 156 (1994), 215–216.Google Scholar
[4] Banuelos, R. and Van Den Berg, M., Dirichlet eigenfunctions for horn-shaped regions and Laplacians on crosssections. J. London Math. Soc., to appear.Google Scholar
[5] Berger, G., Asymptotische Eigenwertverteilung des Laplace-Operators in bestimmten unbeschrankten Gebieten mit Neumannschen Randbedingungen und Restgliedabschatzungen. Z. Anal. Anwendungen, (1) 4 (1985), 85–96.Google Scholar
[6] Davies, E. B. and Simon, B., Ultracontractivity and heat kernels for Schrodinger operators and Dirichlet Laplacians. J. Funct. Anal. 59 (1984), 335–395.Google Scholar
[7] Davies, E. B. and Simon, B., Spectral properties of the Neumann Laplacian on horns. Geom. Funct. Anal. (1) 2 (1992), 105–117.Google Scholar
[8] Edward, J., Spectral theory for the Neumann Laplacian on planar domains with horn-like ends. Canad. J.Math. (2) 49 (1997), 232–262.Google Scholar
[9] Edward, J., Spectrum of the Neumann Laplacian on aymptotically perturbed waveguides. unpublished work.Google Scholar
[10] Edward, J., Eigenfunction decay and eigenvalue accumulation for the Laplacian on asymptotically perturbed waveguides. J. London Math. Soc., to appear.Google Scholar
[11] Edward, J., Corrigendum to “Spectral theory for the Neumann Laplacian on planar domains with horn-like ends”. Canad. J. Math., 51 (2000), 119–122.Google Scholar
[12] Evans, W. D. and Harris, D. J., Sobolev embeddings for generalised ridge domains. Proc. London Math. Soc. (3) 54 (1987), 141–175.Google Scholar
[13] Jaksic, V., On the Spectrum of Neumann Laplacian of Long Range Horns: A note on Davies-Simon Theorem. Proc. Amer.Math. Soc. 119 (1993), 663–669.Google Scholar
[14] Jaksic, V., Molcanov, S. and Simon, B., Eigenvalue asymptotics of the Neumann Laplacian of regions and manifolds with cusps. J. Funct. Anal. (1) 106 (1992), 59–79.Google Scholar
[15] Reed, M. and Simon, B., Methods of modern mathematical physics. Vol 4, Academic Press, 1978.Google Scholar