Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yaldız, Hatice
and
Agarwal, Praveen
2017.
s-convex functions on discrete time domains.
Analysis,
Vol. 37,
Issue. 4,
Arslan, Aykut
2017.
Discrete convexity and its characterization via the fractional Hermite–Hadamard inequality.
Analysis,
Vol. 37,
Issue. 3,
p.
169.
Atıcı, Ferhan M.
and
Yaldız, Hatice
2018.
Refinements on the discrete Hermite–Hadamard inequality.
Arabian Journal of Mathematics,
Vol. 7,
Issue. 3,
p.
175.
Dahal, Rajendra
and
Goodrich, Christopher S.
2019.
A uniformly sharp convexity result for discrete fractional sequential differences.
Rocky Mountain Journal of Mathematics,
Vol. 49,
Issue. 8,
Kashuri, Artion
Mohammed, Pshtiwan Othman
Abdeljawad, Thabet
Hamasalh, Faraidun
Chu, Yuming
and
Ahmad, Imtiaz
2020.
New Simpson Type Integral Inequalities for
s
-Convex Functions and Their Applications.
Mathematical Problems in Engineering,
Vol. 2020,
Issue. ,
p.
1.
Goodrich, Christopher
and
Lizama, Carlos
2020.
A transference principle for nonlocal operators using a convolutional approach: fractional monotonicity and convexity.
Israel Journal of Mathematics,
Vol. 236,
Issue. 2,
p.
533.
Abdeljawad, Thabet
Mohammed, Pshtiwan Othman
and
Kashuri, Artion
2020.
New Modified Conformable Fractional Integral Inequalities of Hermite–Hadamard Type with Applications.
Journal of Function Spaces,
Vol. 2020,
Issue. ,
p.
1.
Srivastava, Hari Mohan
Kashuri, Artion
Mohammed, Pshtiwan Othman
and
Nonlaopon, Kamsing
2021.
Certain Inequalities Pertaining to Some New Generalized Fractional Integral Operators.
Fractal and Fractional,
Vol. 5,
Issue. 4,
p.
160.
Srivastava, Hari Mohan
Kashuri, Artion
Mohammed, Pshtiwan Othman
Baleanu, Dumitru
and
Hamed, Y. S.
2021.
Fractional Integral Inequalities for Exponentially Nonconvex Functions and Their Applications.
Fractal and Fractional,
Vol. 5,
Issue. 3,
p.
80.
Mohammed, Pshtiwan Othman
Abdeljawad, Thabet
Alqudah, Manar A.
and
Jarad, Fahd
2021.
New discrete inequalities of Hermite–Hadamard type for convex functions.
Advances in Difference Equations,
Vol. 2021,
Issue. 1,
Goodrich, Christopher S.
Jonnalagadda, Jagan M.
and
Lyons, Benjamin
2021.
Convexity, monotonicity, and positivity results for sequential fractional nabla difference operators with discrete exponential kernels.
Mathematical Methods in the Applied Sciences,
Vol. 44,
Issue. 8,
p.
7099.
Dahal, Rajendra
and
Goodrich, Christopher S.
2021.
Analysis of convexity results for discrete fractional nabla operators.
Rocky Mountain Journal of Mathematics,
Vol. 51,
Issue. 6,
Mohammed, Pshtiwan Othman
Ryoo, Cheon Seoung
Kashuri, Artion
Hamed, Y. S.
and
Abualnaja, Khadijah M.
2021.
Some Hermite–Hadamard and Opial dynamic inequalities on time scales.
Journal of Inequalities and Applications,
Vol. 2021,
Issue. 1,
Goodrich, Christopher S.
Lyons, Benjamin
Scapellato, Andrea
and
Velcsov, Mihaela T.
2021.
Analytical and numerical convexity results for discrete fractional sequential differences with negative lower bound.
Journal of Difference Equations and Applications,
Vol. 27,
Issue. 3,
p.
317.
Bravo, Jennifer
Lizama, Carlos
and
Rueda, Silvia
2022.
Qualitative properties of nonlocal discrete operators.
Mathematical Methods in the Applied Sciences,
Vol. 45,
Issue. 10,
p.
6346.
QI, YONGFANG
WEN, QINGZHI
LI, GUOPING
XIAO, KECHENG
and
WANG, SHAN
2022.
DISCRETE HERMITE–HADAMARD-TYPE INEQUALITIES FOR (s,m)-CONVEX FUNCTION.
Fractals,
Vol. 30,
Issue. 07,
BOHNER, Martin
KASHURİ, Artion
MOHAMMED, Pshtiwan
and
NAPOLES VALDES, Juan Eduardo
2022.
Hermite-Hadamard-type inequalities for conformable integrals.
Hacettepe Journal of Mathematics and Statistics,
Vol. 51,
Issue. 3,
p.
775.
Wang, Qiushuang
and
Xu, Run
2022.
Generalized Hermite-Hadamard Inequalities on Discrete Time Scales.
Fractal and Fractional,
Vol. 6,
Issue. 10,
p.
563.
Kashuri, Artion
Sahoo, Soubhagya Kumar
Kodamasingh, Bibhakar
Tariq, Muhammad
Hamoud, Ahmed A.
Emadifar, Homan
Hamasalh, Faraidun K.
Mohammed, Nedal M.
Khademi, Masoumeh
and
Wang, Guotao
2022.
Integral Inequalities of Integer and Fractional Orders for n–Polynomial Harmonically tgs–Convex Functions and Their Applications.
Journal of Mathematics,
Vol. 2022,
Issue. 1,
Liko, Rozana
Mohammed, Pshtiwan Othman
Kashuri, Artion
and
Hamed, Y. S.
2022.
Reverse Minkowski Inequalities Pertaining to New Weighted Generalized Fractional Integral Operators.
Fractal and Fractional,
Vol. 6,
Issue. 3,
p.
131.
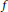 $f$
defined on the set of integers,
$f$
defined on the set of integers,
 $\mathbb{Z}$
. We prove that
$\mathbb{Z}$
. We prove that
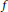 $f$
is convex on
$f$
is convex on
 $\mathbb{Z}$
if and only if
$\mathbb{Z}$
if and only if
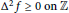 ${{\Delta }^{2}}f\,\ge \,0$
on
${{\Delta }^{2}}f\,\ge \,0$
on
 $\mathbb{Z}$
. As a first application of this new concept, we state and prove discrete Hermite–Hadamard inequality using the basics of discrete calculus (i.e., the calculus on
$\mathbb{Z}$
. As a first application of this new concept, we state and prove discrete Hermite–Hadamard inequality using the basics of discrete calculus (i.e., the calculus on
 $\mathbb{Z}$
). Second, we state and prove the discrete fractional Hermite–Hadamard inequality using the basics of discrete fractional calculus. We close the paper by defining the convexity of a real valued function on any time scale.
$\mathbb{Z}$
). Second, we state and prove the discrete fractional Hermite–Hadamard inequality using the basics of discrete fractional calculus. We close the paper by defining the convexity of a real valued function on any time scale.

