Article contents
An Existence Theory for Incomplete Designs
Published online by Cambridge University Press: 20 November 2018
Abstract
An incomplete pairwise balanced design is equivalent to a pairwise balanced design with a distinguished block, viewed as a ‘hole’. If there are v points, a hole of size
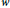 $w$
, and all (other) block sizes equal
$w$
, and all (other) block sizes equal
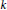 $k$
, this is denoted
$k$
, this is denoted
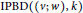 $\text{IPBD}\left( \left( v;w \right),\,k \right)$
. In addition to congruence restrictions on
$\text{IPBD}\left( \left( v;w \right),\,k \right)$
. In addition to congruence restrictions on
 $v$
and
$v$
and
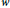 $w$
, there is also a necessary inequality:
$w$
, there is also a necessary inequality:
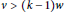 $v\,>\,\left( k\,-\,1 \right)w$
. This article establishes two main existence results for
$v\,>\,\left( k\,-\,1 \right)w$
. This article establishes two main existence results for
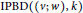 $\text{IPBD}\left( \left( v;w \right),\,k \right)$
: one in which
$\text{IPBD}\left( \left( v;w \right),\,k \right)$
: one in which
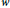 $w$
is fixed and
$w$
is fixed and
 $v$
is large, and the other in the case
$v$
is large, and the other in the case
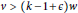 $v>\,\left( k-1+\varepsilon \right)w$
when
$v>\,\left( k-1+\varepsilon \right)w$
when
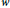 $w$
is large (depending on
$w$
is large (depending on
 $\varepsilon$
). Several possible generalizations of the problemare also discussed.
$\varepsilon$
). Several possible generalizations of the problemare also discussed.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 3
- Cited by


