Hostname: page-component-7bb8b95d7b-l4ctd Total loading time: 0 Render date: 2024-09-22T04:49:32.036Z Has data issue: false hasContentIssue false
  • English
  • Français

Additive Families of Low Borel Classes and Borel Measurable Selectors

Published online by Cambridge University Press:  20 November 2018

J. Spurný  and
M. Zelený
J. Spurný
Affiliation:
Faculty of Mathematics and Physics, Charles University, Sokolovská 83, Czech Republice-mail: spurny@karlin.mff.cuni.czzeleny@karlin.mff.cuni.cz
M. Zelený
Affiliation:
Faculty of Mathematics and Physics, Charles University, Sokolovská 83, Czech Republice-mail: spurny@karlin.mff.cuni.czzeleny@karlin.mff.cuni.cz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An important conjecture in the theory of Borel sets in non-separable metric spaces is whether any point-countable Borel-additive family in a complete metric space has a $\sigma $-discrete refinement. We confirm the conjecture for point-countable 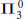$\Pi _{3}^{0}$-additive families, thus generalizing results of R. W. Hansell and the first author. We apply this result to the existence of Borel measurable selectors for multivalued mappings of low Borel complexity, thus answering in the affirmative a particular version of a question of J. Kaniewski and R. Pol.

Keywords

54H0554E35σ-discrete refinementBorel-additive familymeasurable selection
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 1 , 01 March 2011 , pp. 180 - 192
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Engelking, R., General topology. Sigma Series in Pure Mathematics, 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[2] Fleissner, W. G., An axiom for nonseparable Borel theory. Trans. Amer. Math. Soc. 251(1979), 309–328. doi:10.2307/1998696Google Scholar
[3] Fremlin, D. H., Measure-additive coverings and measurable selectors. Dissertationes Math. 260(1987), 116 pp.Google Scholar
[4] Hansell, R. W., Borel measurable mappings for nonseparable metric spaces. Trans. Amer. Math. Soc. 161(1971), 145–169. doi:10.2307/1995934Google Scholar
[5] Hansell, R. W., On characterizing non-separable analytic and extended Borel sets as types of continuous images. Proc. London. Math. Soc. 28(1974), 683–699. doi:10.1112/plms/s3-28.4.683Google Scholar
[6] Hansell, R. W., Point-countable Souslin-additive families and σ–discrete reductions. In: General topology and its relation to modern analysis and algebra. V. (Prague, 1981), Sigma Series in Pure Mathematics, 3, Heldermann, Berlin, 1983, pp. 254–260.Google Scholar
[7] Hansell, R. W., Hereditarily additive families in descriptive set theory and Borel measurable multimaps. Trans. Amer. Math. Soc. 278(1983), no. 2, 725–749. doi:10.2307/1999181Google Scholar
[8] Hansell, R. W., A measurable selection and representation theorem in nonseparable spaces. In: Measure theory, Oberwolfach 1983, Lecture Notes in Math., 1089, Springer, Berlin, 1984, pp. 86–94.Google Scholar
[9] Hansell, R. W., Fσ-set covers of analytic spaces and first class selectors. Proc. Amer. Math. Soc. 96(1986), no. 2, 365–371. doi:10.2307/2046182Google Scholar
[10] Hansell, R. W., Nonseparable analytic metric spaces and quotient maps. Topology Appl. 85(1998), no. 1–3, 143–152. doi:10.1016/S0166-8641(97)00146-6Google Scholar
[11] Kaniewski, J. and Pol, R., Borel-measurable selectors for compact-valued mappings in the non-separable case. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 23(1975), no. 10, 1043–1050.Google Scholar
[12] Kechris, A. S., Classical descriptive set theory. Graduate Texts in Mathematics, 156, Springer-Verlag, New York, 1995.Google Scholar
[13] Pol, R., Note on decompositions of metrizable spaces. II. Fund. Math. 100(1978), no. 2, 129–143.Google Scholar
[14] Rogers, C. E. and Jayne, J. E., K-analytic sets. In: Analytic sets, Academic Press, London, 1980, pp. 1–181.Google Scholar
[15] Spurný, J., Fσ-additive families and the invariance of Borel classes. Proc. Amer. Math. Soc. 133(2005), no. 3, 905–915. doi:10.1090/S0002-9939-04-07587-2Google Scholar
[16] Spurný, J., Gδ-additive families in absolute Souslin spaces and Borel measurable selectors. Topology Appl. 154(2007), no. 15, 2779–2785. doi:10.1016/j.topol.2007.05.012Google Scholar
[17] Stone, A. H., Nonseparable Borel sets. II. General Topology and Appl. 2(1972), 249–270. doi:10.1016/0016-660X(72)90010-4Google Scholar
[18] Stone, A. H., Analytic sets in non-separable metric spaces. In: Analytic sets, Academic Press, London, 1980, pp. 471–480.Google Scholar