No CrossRef data available.
Published online by Cambridge University Press: 10 June 2019
We introduce the notion of Lie invariant structure Jacobi operators for real hypersurfaces in the complex quadric 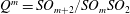 $Q^{m}=SO_{m+2}/SO_{m}SO_{2}$. The existence of invariant structure Jacobi operators implies that the unit normal vector field
$Q^{m}=SO_{m+2}/SO_{m}SO_{2}$. The existence of invariant structure Jacobi operators implies that the unit normal vector field 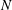 $N$ becomes
$N$ becomes 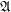 $\mathfrak{A}$-principal or
$\mathfrak{A}$-principal or 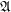 $\mathfrak{A}$-isotropic. Then, according to each case, we give a complete classification of real hypersurfaces in
$\mathfrak{A}$-isotropic. Then, according to each case, we give a complete classification of real hypersurfaces in 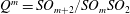 $Q^{m}=SO_{m+2}/SO_{m}SO_{2}$ with Lie invariant structure Jacobi operators.
$Q^{m}=SO_{m+2}/SO_{m}SO_{2}$ with Lie invariant structure Jacobi operators.
This work was supported by grant Proj. No. NRF-2018-R1D1A1B-05040381 and the second by grant Proj. No. NRF-2018-R1A6A3A-01011828 from National Research Foundation of Korea. Young Jin Suh is the corresponding author.