Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
EnglishFrançais
Canadian Mathematical Bulletin Canadian Mathematical Bulletin

Article contents

Non-spectral Problem for Some Self-similar Measures

Part of: Classical measure theory Nontrigonometric harmonic analysis Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  28 August 2019

Ye Wang ,
Xin-Han Dong  and
Yue-Ping Jiang
Ye Wang
Affiliation:
College of Mathematics and Econometrics, Hunan University, Changsha, Hunan 410082, P.R. China Department of Mathematics, The University of Iowa, Iowa City, IA 52242, USA Email: hnsdwangye@163.com
Xin-Han Dong
Affiliation:
College of Mathematics and Econometrics, Hunan University, Changsha, Hunan 410082, P.R. China Email: xhdonghnsd@163.comypjiang731@163.com
Yue-Ping Jiang
Affiliation:
College of Mathematics and Econometrics, Hunan University, Changsha, Hunan 410082, P.R. China Email: xhdonghnsd@163.comypjiang731@163.com
Corresponding
E-mail address:
hnsdwangye@163.com
xhdonghnsd@163.com
ypjiang731@163.com
Get access
Rights & Permissions[Opens in a new window]

Abstract

Suppose that 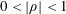$0<|\unicode[STIX]{x1D70C}|<1$ and 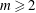$m\geqslant 2$ is an integer. Let 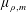$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70C},m}$ be the self-similar measure defined by 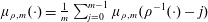$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70C},m}(\cdot )=\frac{1}{m}\sum _{j=0}^{m-1}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70C},m}(\unicode[STIX]{x1D70C}^{-1}(\cdot )-j)$ . Assume that 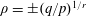$\unicode[STIX]{x1D70C}=\pm (q/p)^{1/r}$ for some 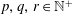$p,q,r\in \mathbb{N}^{+}$ with 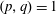$(p,q)=1$ and 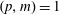$(p,m)=1$ . We prove that if 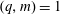$(q,m)=1$ , then there are at most $m$ mutually orthogonal exponential functions in 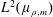$L^{2}(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70C},m})$ and $m$ is the best possible. If 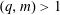$(q,m)>1$ , then there are any number of orthogonal exponential functions in 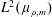$L^{2}(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70C},m})$ .

Keywords

self-similar measure spectral measure orthogonal exponential function Fourier transform

MSC classification

Primary: 28A80: Fractals
Secondary: 42C05: Orthogonal functions and polynomials, general theory 46C05: Hilbert and pre-Hilbert spaces
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 2 , June 2020 , pp. 318 - 327
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below.
If you should have access and can't see this content please contact technical support.

Footnotes

The research is supported in part by the NNSF of China (No. 11831007, No.11571099).

References

Dai, X. R., When does a Bernoulli convolution admit a spectrum? Adv. Math. 231(2012), 1681–1693. https://doi.org/10.1016/j.aim.2012.06.026CrossRefGoogle Scholar
Dai, X. R., He, X. G., and Lau, K. S., On spectral N-Bernoulli measures. Adv. Math. 259(2014), 511–531. https://doi.org/10.1016/j.aim.2014.03.026CrossRefGoogle Scholar
Dai, X. R. and Sun, Q. Y., Spectral measures with arbitrary Hausdorff dimensions. J. Funct. Anal. 268(2015), 2464–2477. https://doi.org/10.1016/j.jfa.2015.01.005CrossRefGoogle Scholar
Deng, Q. R., Spectrality of one dimensional self-similar measures with consecutive digits. J. Math. Anal. Appl. 409(2014), 331–346. https://doi.org/10.1016/j.jmaa.2013.07.046CrossRefGoogle Scholar
Dutkay, D., Emami, S., and Lai, C. K., Existence and exactness of exponential Riesz sequences and frames for fractal measures. arxiv:1809.06541Google Scholar
Dutkay, D., Han, D., and Sun, Q. Y., On the spectra of a Cantor measure. Adv. Math. 221(2009), 251–276. https://doi.org/10.1016/j.aim.2008.12.007CrossRefGoogle Scholar
Hu, T. Y. and Lau, K. S., Spectral property of the Bernoulli convolutions. Adv. Math. 219(2008), 554–567. https://doi.org/10.1016/j.aim.2008.05.004CrossRefGoogle Scholar
Jorgensen, P. and Pedersen, S., Dense analytic subspaces in fractal L 2-spaces. J. Anal. Math. 75(1998), 185–228. https://doi.org/10.1007/BF02788699CrossRefGoogle Scholar
Karpilovsky, G., Topics in field theory. North-Holland Publishing Co., Amsterdam, 1989.Google Scholar
Ke, Z. and Sun, Q., Lectures of the theory of numbers. Higher Education Press, Beijing, 2003.Google Scholar
Łaba, I. and Wang, Y., On spectral Cantor measures. J. Funct. Anal. 193(2002), 409–420. https://doi.org/10.1006/jfan.2001.3941CrossRefGoogle Scholar
Lai, C. K. and Wang, Y., Non-spectral fractal measures with fourier frames. J. Fractal Geom. 4(2017), 305–327. https://doi.org/10.4171/JFG/52CrossRefGoogle Scholar
Li, J. L., Spectra of a class of self-affine measures. J. Funct. Anal. 260(2011), 1086–1095. https://doi.org/10.1016/j.jfa.2010.12.001CrossRefGoogle Scholar
Liu, J. C., Dong, X. H., and Li, J. L., Non-spectral problem for the planar self-affine measures. J. Funct. Anal. 273(2017), 705–720. https://doi.org/10.1016/j.jfa.2017.04.003CrossRefGoogle Scholar
Strichartz, R., Convergence of Mock Fourier series. J. Anal. Math. 99(2006), 333–353. https://doi.org/10.1007/BF02789451CrossRefGoogle Scholar
Solomyak, B., Notes on Bernoulli convolutions. In: Fractal geometry and applications: A Jubilee of Benoît Mandelbrot. Part 1. Proc. Sympos. Pure Math., 72, American Mathematical Society, Providence, RI, 2004, pp. 207–230.10.1090/pspum/072.1/2112107CrossRefGoogle Scholar
Wang, Z. Y., Wang, Z. M., Dong, X. H., and Zhang, P. F., Orthogonal exponential functions of self-similar measures with consecutive digits in ℝ. J. Math. Anal. Appl. 467(2018), 1148–1152. https://doi.org/10.1016/j.jmaa.2018.07.062CrossRefGoogle Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 58 *
View data table for this chart

* Views captured on Cambridge Core between 28th August 2019 - 28th January 2021. This data will be updated every 24 hours.

Hostname: page-component-6585876b8c-d5djx Total loading time: 0.399 Render date: 2021-01-28T16:21:47.300Z Query parameters: { "hasAccess": "0", "openAccess": "0", "isLogged": "0", "lang": "en" } Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": false }

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Non-spectral Problem for Some Self-similar Measures
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Non-spectral Problem for Some Self-similar Measures
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Non-spectral Problem for Some Self-similar Measures
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *