Research Article
Sets on which Measurable Functions are Determined by their Range
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1089-1116
-
- Article
-
- You have access
- Export citation
Classifying Pl 5-Manifolds by Regular Genus: The Boundary Case
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 193-211
-
- Article
-
- You have access
- Export citation
Maps in Locally Orientable Surfaces and Integrals Over Real Symmetric Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 865-882
-
- Article
-
- You have access
- Export citation
Characteristic Cycles in Hermitian Symmetric Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-467
-
- Article
-
- You have access
- Export citation
Sweeping Out Properties of Operator Sequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-23
-
- Article
-
- You have access
- Export citation
Fine Spectra and Limit Laws, II First-Order 0–1 Laws
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 641-652
-
- Article
-
- You have access
- Export citation
Proof of a Conjecture of Goulden and Jackson
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 883-886
-
- Article
-
- You have access
- Export citation
On q-Carleson Measures for Spaces of M-Harmonic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 653-674
-
- Article
-
- You have access
- Export citation
Differential Equations Defined by the Sum of two Quasi-Homogeneous Vector Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 212-231
-
- Article
-
- You have access
- Export citation
The Von Neumann Algebra VN(G) of a Locally Compact Group and Quotients of Its Subspaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1117-1138
-
- Article
-
- You have access
- Export citation
Spatial Branching Processes and Subordination
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 24-54
-
- Article
-
- You have access
- Export citation
Fine Spectra and Limit Laws I. First-Order Laws
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 468-498
-
- Article
-
- You have access
- Export citation
Polynomials With {0, +1, -1} Coefficients and a Root Close to a Given Point
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 887-915
-
- Article
-
- You have access
- Export citation
Spectral Theory for the Neumann Laplacian on Planar Domains With Horn-Like Ends
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 232-262
-
- Article
-
- You have access
- Export citation
Gorenstein Witt Rings II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 499-519
-
- Article
-
- You have access
- Export citation
Normal Functions: Lp Estimates
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 55-73
-
- Article
-
- You have access
- Export citation
Majorations Effectives Pour L’ Équation de Fermat Généralisée
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1139-1161
-
- Article
-
- You have access
- Export citation
Some Adjunction-Theoretic Properties of Codimension Two Non-Singular Subvarities of Quadrics
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 675-695
-
- Article
-
- You have access
- Export citation
Determinantal Forms for Symplectic and Orthogonal Schur Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 263-282
-
- Article
-
- You have access
- Export citation
Classical Orthogonal Polynomials as Moments
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 520-542
-
- Article
-
- You have access
- Export citation



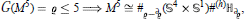
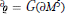 denotes the regular genus of the boundary ∂
denotes the regular genus of the boundary ∂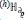 denotes the connected sumof
denotes the connected sumof 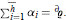 .
.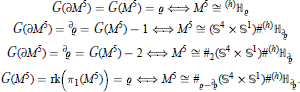
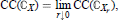
 of
of  of
of