Research Article
A Tauberian Theorem for a Scale of Logarithmic Methods of Summation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-902
-
- Article
-
- You have access
- Export citation
Some Remarks on the Nijenhuis Tensor
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 903-907
-
- Article
-
- You have access
- Export citation
The Cohomology of (Λ2X, ΔX)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 908-921
-
- Article
-
- You have access
- Export citation
Sur Les Anneaux de Groupes Semi-Parfaits
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 922-928
-
- Article
-
- You have access
- Export citation
Chromatic Sums for Rooted Planar Triangulations, IV: The Case λ = ∞
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 929-940
-
- Article
-
- You have access
- Export citation
Frobenius Symbols and the Groups SsGL(n), O(n) and Sp(n)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 941-959
-
- Article
-
- You have access
- Export citation
Residual Finiteness of Commutative Rings and Schemes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 960-972
-
- Article
-
- You have access
- Export citation
FK Spaces in Which the Sequence of Coordinate Vectors is Bounded
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 973-978
-
- Article
-
- You have access
- Export citation
Non-Metrizable Uniformities and Proximities on Metrizable Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 979-981
-
- Article
-
- You have access
- Export citation
The Radius of Convexity of a Linear Combination of Functions in
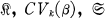 or uα
or uα
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 982-985
-
- Article
-
- You have access
- Export citation
Centers of Infinite Bounded Sets in a Normed Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 986-999
-
- Article
-
- You have access
- Export citation
Correction
Metacyclic Invariants of Knots and Links: Corrigendum
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1000-1001
-
- Article
-
- You have access
- Export citation
Research Article
Direct Sums of Torsion-Free Covers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1002-1005
-
- Article
-
- You have access
- Export citation
On the Isomorphisms Between Certain Congruence Groups, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1006-1014
-
- Article
-
- You have access
- Export citation
Curvature and Radius of Curvature for Functions with Bounded Boundary Rotation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1015-1023
-
- Article
-
- You have access
- Export citation
A Generalization of Čaplygin's Inequality with Applications to Singular Boundary Value Problems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1024-1039
-
- Article
-
- You have access
- Export citation
Strongly and Weakly Non-Poised H-B Interpolation Problems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1040-1050
-
- Article
-
- You have access
- Export citation
The Dual of Frobenius' Reciprocity Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1051-1059
-
- Article
-
- You have access
- Export citation
A Theorem on Permutations of a Finite Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1060-1065
-
- Article
-
- You have access
- Export citation
On Multiplicative Properties of Families of Complexes of Certain Loops
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1066-1077
-
- Article
-
- You have access
- Export citation

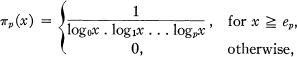
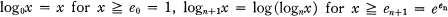 (
(
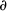 and
and 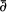 .
.


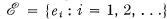 is bounded?” Here
is bounded?” Here 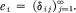 An
An 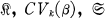 or
or 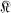 , the normalized convex functions in the unit disc
, the normalized convex functions in the unit disc  has a radius of convexity at least as large as the smallest root of 1 – 3r + 2r
has a radius of convexity at least as large as the smallest root of 1 – 3r + 2r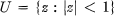 and having the representation
and having the representation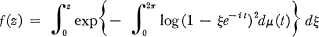
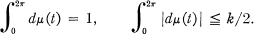

 is a quotient group of a group
is a quotient group of a group