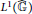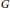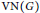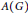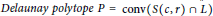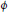Research Article
Dynamics and Regularization of the Kepler Problem on Surfaces of Constant Curvature
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-991
-
- Article
-
- You have access
- Export citation
Classification of Regular Parametrized One-relation Operads
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 992-1035
-
- Article
-
- You have access
- Export citation
Stability for the Brunn-Minkowski and Riesz Rearrangement Inequalities, with Applications to Gaussian Concentration and Finite Range Non-local Isoperimetry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1036-1063
-
- Article
-
- You have access
- Export citation
Amenability and Covariant Injectivity of Locally Compact Quantum Groups II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1064-1086
-
- Article
-
- You have access
- Export citation
Absolute Continuity of Wasserstein Barycenters Over Alexandrov Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1087-1108
-
- Article
-
- You have access
- Export citation
Closed Convex Hulls of Unitary Orbits in Certain Simple Real Rank Zero C* -algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1109-1142
-
- Article
-
- You have access
- Export citation
The Seven Dimensional Perfect Delaunay Polytopes and Delaunay Simplices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1143-1168
-
- Article
-
- You have access
- Export citation
On Residues of Intertwining Operators in Cases with Prehomogeneous Nilradical
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1169-1200
-
- Article
-
- You have access
- Export citation