Research Article
Graphical Regular Representations of Non-Abelian Groups, I
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 993-1008
-
- Article
-
- You have access
- Export citation
Graphical Regular Representations of Non-Abelian Groups, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1009-1018
-
- Article
-
- You have access
- Export citation
Cohomology Theorems for Borel-Like Solvable Lie Algebras in Arbitrary Characteristic
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1019-1026
-
- Article
-
- You have access
- Export citation
𝔪-Stone Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1027-1032
-
- Article
-
- You have access
- Export citation
Moore Spaces, Semi-Metric Spaces and Continuous Mappings Connected with Them
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1033-1042
-
- Article
-
- You have access
- Export citation
Products of Locally Compact Groups with Zero and Their Actions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1043-1051
-
- Article
-
- You have access
- Export citation
Multiplications on a Space with Finitely Many Non-Vanishing Homotopy Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1052-1062
-
- Article
-
- You have access
- Export citation
An Application of Ultraproducts to Lattice-Ordered Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1063-1064
-
- Article
-
- You have access
- Export citation
Automorphism Groups of Algebras of Finite Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1065-1069
-
- Article
-
- You have access
- Export citation
The Friedberg-Muchnik Theorem Re-Examined
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1070-1078
-
- Article
-
- You have access
- Export citation
Domains of Paracompactness and Regularity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1079-1085
-
- Article
-
- You have access
- Export citation
On a Theorem of Cohen and Lyndon About Free Bases for Normal Subgroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1086-1091
-
- Article
-
- You have access
- Export citation
Degrees in Which the Recursive Sets are Uniformly Recursive
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1092-1099
-
- Article
-
- You have access
- Export citation
Modular Hadamard Matrices and Related Designs, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1100-1109
-
- Article
-
- You have access
- Export citation
Sequentially Relatively Uniformly Complete Riesz Spaces and Vulikh Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1110-1113
-
- Article
-
- You have access
- Export citation
Some Properties of Anosov Flows
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1114-1121
-
- Article
-
- You have access
- Export citation
Properties of Quotient Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1122-1128
-
- Article
-
- You have access
- Export citation
Presentations of the Groups SL(2, m) And PSL(2, m)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1129-1131
-
- Article
-
- You have access
- Export citation
Extension Closed and Cluster Closed Subspaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1132-1136
-
- Article
-
- You have access
- Export citation
Group Rings with Only Trivial Units of Finite Order
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1137-1138
-
- Article
-
- You have access
- Export citation



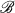 of topological spaces and a class
of topological spaces and a class 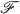 of maps of topological spaces, our interest is in characterization of the class
of maps of topological spaces, our interest is in characterization of the class  (
(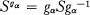 and
and