Article contents
The Universal Theory of Ordered Equidecomposability Types Semigroups
Published online by Cambridge University Press: 20 November 2018
Abstract
We prove that a commutative preordered semigroup embeds into the space of all equidecomposability types of subsets of some set equipped with a group action (in short, a full type space) if and only if it satisfies the following axioms: (i) (⩝x,y) (x ≤ x + y); (ii) (⩝x,y)((x ≤ y and y ≤ x) ⇒ x = y); (iii) (⩝x,y,u, v)((x + u ≤ y + u and u ≤ v) ⩝ x + v ≤ y ≤ v); (iv) (⩝x, u, V)((x + u = u and u ≤ v) ⇒ x + v = v); (v) (⩝x,y)(mx ≤ my ⇒ x ≤ y) (all m ∊ Ν \ {0}). Furthermore, such a structure can always be embedded into a reduced power of the space Τ of nonempty initial segments of 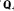 + with rational (possibly infinite) endpoints, equipped with the addition defined by
+ with rational (possibly infinite) endpoints, equipped with the addition defined by 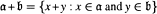 and the ordering defined by
and the ordering defined by 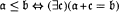 . As a corollary, the set of all universal formulas of (+, ≤) satisfied by all full type spaces is decidable.
. As a corollary, the set of all universal formulas of (+, ≤) satisfied by all full type spaces is decidable.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1994
References
- 5
- Cited by


