Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-18T12:05:18.864Z Has data issue: false hasContentIssue false
  • English
  • Français

Unitary representations of type B rational Cherednik algebras and crystal combinatorics

Part of: Representation theory of rings and algebras Lie algebras and Lie superalgebras Representation theory of groups Rings and algebras arising under various constructions Algebraic combinatorics

Published online by Cambridge University Press:  29 September 2021

Emily Norton Open the ORCID record for Emily Norton [Opens in a new window]
Emily Norton*
Affiliation:
School of Mathematics, Statistics and Actuarial Science, Sibson Building, Parkwood Road, University of Kent, Canterbury, Kent CT2 7FS
*
e-mail: E.Norton@kent.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We compare crystal combinatorics of the level 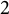$2$ Fock space with the classification of unitary irreducible representations of type B rational Cherednik algebras to study how unitarity behaves under parabolic restriction. We show that the crystal operators that remove boxes preserve the combinatorial conditions for unitarity, and that the parabolic restriction functors categorifying the crystals send irreducible unitary representations to unitary representations. Furthermore, we find the supports of the unitary representations.

Keywords

rational Cherednik algebraunitary representationFock spaceaffine Lie algebra crystalcombinatorial representation theory

MSC classification

Primary: 16G99: None of the above, but in this section
Secondary: 05E10: Combinatorial aspects of representation theory 17B37: Quantum groups (quantized enveloping algebras) and related deformations 20C08: Hecke algebras and their representations 16S80: Deformations of rings
Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 1 , February 2023 , pp. 140 - 169
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Part of this work was carried out under the auspices of the grant SFB-TRR 195.

References

Berest, Y., Etingof, P., and Ginzburg, V., Finite-dimensional representations of rational Cherednik algebras. Int. Math. Res. Not. IMRN 19(2003), 1053–1088.CrossRefGoogle Scholar
Berkesch Zamaere, C., Griffeth, S., and Sam, S. V., Jack polynomials as fractional quantum Hall states and the Betti numbers of the $\left(k+1\right)$ -equals ideal. Comm. Math. Phys. 330(2014), no. 1, 415–434.CrossRefGoogle Scholar
Bezrukavnikov, R. and Etingof, P., Parabolic induction and restriction functors for rational Cherednik algebras. Selecta Math. (N.S.). 14(2009), nos. 3–4, 397–425.CrossRefGoogle Scholar
Bowman, C. and Cox, A. G., Modular decomposition numbers of cyclotomic Hecke and diagrammatic Cherednik algebras: a path theoretic approach. Forum Math. Sigma. 6(2018), e11.Google Scholar
Bowman, C., Cox, A. G., and Hazi, A., Path isomorphisms between quiver Hecke and diagrammatic Bott–Samelson endomorphism algebras. Preprint, 2021. arXiv:2005.02825 Google Scholar
Bowman, C., Hazi, A., and Norton, E., The modular Weyl–Kac character formula. Preprint, 2020. arXiv:2004.13082 Google Scholar
Bowman, C., Norton, E., and Simental, J., Characteristic-free bases and BGG resolutions of unitary simple modules for quiver Hecke and Cherednik algebras. Preprint, 2018. arXiv:1803:08736 Google Scholar
Chuang, J. and Miyachi, H., Runner removal Morita equivalences. In Representation theory of algebraic groups and quantum groups, Progr. Math., 284, Birkhäuser/Springer, New York, (editor: Gyoja, Akihiko, Nakajima, Hiraku, Shinoda, Ken-ichi, Shoji, Toshiaki, Tanisaki, Toshiyuki) 2010, pp. 55–79.CrossRefGoogle Scholar
Chuang, J. and Rouquier, R., Derived equivalences for symmetric groups and ${sl}_2$ -categorifications. Ann. Math. (2). 167(2008), no. 1, 245–298.CrossRefGoogle Scholar
Etingof, P. and Ginzburg, V., Symplectic reflection algebras, Calogero–Moser space, and deformed Harish–Chandra homomorphism. Invent. Math. 147(2002), no. 2, 243–348.CrossRefGoogle Scholar
Etingof, P. and Stoica, E., Unitary representations of rational Cherednik algebras. Represent. Theory. 13(2009), 349–370, With an appendix by S. Griffeth.CrossRefGoogle Scholar
Fishel, S., Griffeth, S., and Manosalva, E., Unitary representations of the rational Cherednik algebra: $V$ -homology. Math. Z. 299(2021), 2215–2255 Preprint, 2020. arXiv:2008.04412 CrossRefGoogle Scholar
Gerber, T., Triple crystal action in Fock spaces. Adv. Math. 329(2018), 916–954.CrossRefGoogle Scholar
Gerber, T., Heisenberg algebra, wedges and crystals. J. Algebraic Combin. 49(2019), no. 1, 99–124.Google Scholar
Gerber, T. and Norton, E., The ${sl}_{\infty }$ -crystal combinatorics of higher level Fock spaces. J. Comb. Algebra. 2(2018), no. 2, 103–145.CrossRefGoogle Scholar
Ginzburg, V., Guay, N., Opdam, E., and Rouquier, R., On the category $\mathcal{O}$ for rational Cherednik algebras. Invent. Math. 154(2007), 617–651.CrossRefGoogle Scholar
Gorsky, E., Simental, J., and Vazirani, M., Parabolic Hilbert schemes via the Dunkl–Opdam subalgebra. Preprint, 2020. arXiv:2004.14873 Google Scholar
Griffeth, S., Orthogonal functions generalizing Jack polynomials. Trans. Amer. Math. Soc. 362(2010), no. 11, 6131–6157.Google Scholar
Griffeth, S., Unitary representations of cyclotomic rational Cherednik algebras. J. Algebra. 512(2018), 310–356.CrossRefGoogle Scholar
Griffeth, S., Gusenbauer, A., Juteau, D., and Lanini, M., Parabolic degeneration of rational Cherednik algebras. Selecta Math. 23(2017), no. 4, 2705–2754.Google Scholar
Jacon, N. and Lecouvey, C., A combinatorial decomposition of higher level Fock spaces. Osaka J. Math. 50(2013), no. 4, 897–920.Google Scholar
Jimbo, M., Misra, K. C., Miwa, T., and Okado, M., Combinatorics of representations of ${U}_q(\hat{sl(n)})$ at q = 0. Comm. Math. Phys. 136(1991), no. 3, 543–566.CrossRefGoogle Scholar
Losev, I., Rational Cherednik algebras and categorification . In: Beliakova, A. and Lauda, A. (eds.), Categorification and higher representation theory, Contemp. Math. 683, Amer. Math. Soc., Providence, RI, 2017, 1–41.Google Scholar
Losev, I., Supports of simple modules in cyclotomic Cherednik categories O. Advances in Mathematics 377(2021), 107491 Preprint, 2020. arXiv:1509.00526 Google Scholar
Montarani, S., On some finite dimensional representations of symplectic reflection algebras associated to wreath products. Comm. Algebra. 35(2007), no. 5, 1449–1467.CrossRefGoogle Scholar
Rouquier, R., q-Schur algebras and complex reflection groups. Mosc. Math. J. 8 (2008), no. 1, 119–158, 184.CrossRefGoogle Scholar
Ruff, O., Completely splittable representations of symmetric groups and affine Hecke algebras. J. Algebra. 305(2006), no. 2, 1197–1211.CrossRefGoogle Scholar
Shan, P., Crystals of Fock spaces and cyclotomic rational double affine Hecke algebras. Ann. Sci. Éc. Norm. Supér. 44(2011), 147–182.Google Scholar
Shan, P. and Vasserot, E., Heisenberg algebras and rational double affine Hecke algebras. J. Amer. Math. Soc. 25(2012), no. 4, 959–1031.CrossRefGoogle Scholar
Shelley-Abrahamson, S., The Dunkl weight function for rational Cherednik algebras. Selecta Math. 26(2020), 8.CrossRefGoogle Scholar
Wilcox, S., Supports of representations of the rational Cherednik algebra of type A. Adv. Math. 314(2017), 426–492.CrossRefGoogle Scholar