Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-19T22:13:41.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Tractable Fields

Published online by Cambridge University Press:  20 November 2018

M. Chacron ,
J.-P. Tignol  and
A. R. Wadsworth
M. Chacron
Affiliation:
Department of Mathematics, Carleton University, Ottawa, Ontario, K1S 5B6
J.-P. Tignol
Affiliation:
Institut de Mathématique Pure et Appliquée, Université Catholique de Louvain, Chemin du Cyclotron, 2, B-1348 Louvain-la-Neuve, Belgium email: tignol@agel.ucl.ac.be
A. R. Wadsworth
Affiliation:
Department of Mathematics, 0112, University of California at San Diego, 9500 Gilman Drive, La Jolla, California 92093-0112, USA email: arwadsworth@ucsd.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A field 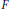$F$ is said to be tractable when a condition described below on the simultaneous representation of quaternion algebras holds over 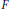$F$. It is shown that a global field 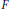$F$ is tractable iff 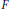$F$ has at most one dyadic place. Several other examples of tractable and nontractable fields are given.

Keywords

12E1511R52
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 1 , 01 February 1999 , pp. 10 - 25
Copyright
Copyright © Canadian Mathematical Society 1999

References

[ART] Amitsur, S., Rowen, L., and Tignol, J.-P., Division algebras of degree 4 and 8 with involution. Israel J. Math. 32 (1979), 133–148.Google Scholar
[A] Artin, E., Algebraic Numbers and Algebraic Functions. Gordon and Breach, New York, 1967.Google Scholar
[Ar] Artin, M., Lipman's proof of resolution of singularities for surfaces. In: Arithmetic Geometry (Eds. Cornell, G. and Silverman, J.), Springer, New York, 1986, 267–287.Google Scholar
[C] Chacron, M., Decomposing and ordering a certain crossed product. Comm. Alg. 21 (1993), 3197–3241.Google Scholar
[CDD] Chacron, M., Dherte, H., and Dixon, J. D., Certain valued involutorial division algebras of exponent 2 and small residue degree. Comm. Algebra 24 (1996), 757–791.Google Scholar
[CTS] Colliot-Thélène, J.-L. and Saito, S., Zéro-cycles sur les variétés p-adiques et groupe de Brauer. Internat. Math. Res. Notices, 1996, 151–160.Google Scholar
[DI] Demeyer, F. and Ingraham, E., Separable Algebras over Commutative Rings. Lecture Notes in Math. 181 , Springer, Berlin, 1971.Google Scholar
[D] Draxl, P., Ostrowski's theoremfor Henselian valued skew fields. J. Reine Angew. Math. 354 (1984), 213–218.Google Scholar
[DK] Draxl, P. and Kneser, M. (Eds.), SK1 von Schiefkörpern. Lecture Notes in Math. 778 , Springer, Berlin, 1980.Google Scholar
[EL1] Elman, R. and Lam, T.-Y., Quadratic forms and the u-invariant. I. Math. Z. 131 (1973), 283–304.Google Scholar
[EL2] Elman, R. and Lam, T.-Y., Quadratic forms under algebraic extensions. Math. Ann. 219 (1976), 21–42.Google Scholar
[ELP] Elman, R., Lam, T.-Y., and Prestel, A., On some Hasse principles over formally real fields. Math. Z. 134 (1973), 291–301.Google Scholar
[FSS] Fein, B., Saltman, D., and Schacher, M., Brauer-Hilbertian fields. Trans. Amer. Math. Soc. 334 (1992), 915–928.Google Scholar
[FJ] Fried, M. and Jarden, M., Field Arithmetic. Springer, Berlin, 1986.Google Scholar
[F] Fröhlich, A., Quadratic forms “à la” local theory. Proc. Cambridge Philos. Soc. 63 (1967), 579–586.Google Scholar
[G] Greenberg, M. J., Lectures on Forms in Many Variables. Benjamin, New York, 1969.Google Scholar
[Gr] Grothendieck, A., Le groupe de Brauer I, II, III. In: Dix exposés sur la cohomologie des schémas (Eds. Grothendieck, A. and Kuiper, N.), North-Holland, Amsterdam, 1968, 46–188.Google Scholar
[H] Han, I., Doctoral Thesis. Univ. of California, San Diego, in preparation.Google Scholar
[JW] Jacob, B. and Wadsworth, A., Division algebras over Henselian fields. J. Algebra 128 (1990), 126–179.Google Scholar
[J] Jacobson, N., Basic Algebra I. Freeman, San Francisco, 1974.Google Scholar
[K] Kaplansky, I., Fröhlich's local quadratic forms. J. Reine Angew. Math. 239 (1969), 74–77.Google Scholar
[L] Lam, T.-Y., The Algebraic Theory of Quadratic Forms (rev. edn). Benjamin, Reading Mass., 1980.Google Scholar
[Li] Lichtenbaum, S., Duality theorems for curves over P-adic fields. Invent. Math. 7 (1969), 120–136.Google Scholar
[M] Milne, J., Étale Cohomology. Princeton Univ. Press, Princeton, NJ, 1980.Google Scholar
[OM] O’Meara, O. T., Introduction to Quadratic Forms. Springer, Berlin, 1963.Google Scholar
[OS] Orzech, M. and Small, C., The Brauer Group of Commutative Rings. Dekker, New York, 1975.Google Scholar
[PY] Platonov, V. and Yanchevskii, V. I., Dieudonné's conjecture on the structure of unitary groups over a division ring, and Hermitian K-theory. Izv. Akad. Nauk SSSR, Ser. Mat. 48 (1984), 1266–1294. English trans., Math. USSR Izvestiya 25 (1985), 573–599.Google Scholar
[Po] Pop, F., Galoissche Kennzeichnung p-adisch abgeschlossener Körper. J. Reine Angew. Math. 392 (1988), 145–175.Google Scholar
[P] Prestel, A., Lectures on Formally Real Fields. Lecture Notes in Math. 1093 , Springer, Berlin, 1984.Google Scholar
[Sa] Saito, S., Arithmetic on two dimensional local rings. Invent. Math. 85 (1986), 379–414.Google Scholar
[S1] Saltman, D., The Brauer group and the center of generic matrices. J. Algebra 97 (1985), 53–67.Google Scholar
[S2] Saltman, D., Division algebras over p-adic curves. J. Ramanujan Math. Soc. 12 (1997), 25–47.Google Scholar
[Sch1] Scharlau, W., Über die Brauer-Gruppe eines algebraischen Funktionenkörpers in einer Variablen. J. Reine Angew. Math. 239/240 (1969), 1–6.Google Scholar
[Sch2] Scharlau, W., Quadratic and Hermitian Forms. Springer, Berlin, 1985.Google Scholar
[Schi] Schilling, O. F. G., The Theory of Valuations. Amer. Math. Soc., Providence, RI, 1950.Google Scholar
[Se] Serre, J.-P., Local fields (English trans. of Corps Locaux). Springer, New York, 1979.Google Scholar
[T] Tate, J., Relations between K2 and Galois cohomology. Invent. Math. 36 (1976), 257–274.Google Scholar
[W1] Wadsworth, A. R., p-Henselian fields: K-theory, Galois cohomology, and graded Witt rings. Pacific J. Math 105 (1983), 473–496.Google Scholar
[W2] Wadsworth, A. R., Extending valuations to finite dimensional division algebras. Proc. Amer. Math. Soc. 98 (1986), 20–22.Google Scholar
[We] Weiss, E., Algebraic Number Theory. Mc Graw-Hill, New York, 1963.Google Scholar
[Wi1] Witt, E., Über ein Gegenbeispiel zum Normensatz. Math. Z. 39 (1935), 462–467.Google Scholar
[Wi2] Witt, E., Theorie der quadratischen Formen in beliebigen Körpern. J. Reine Angew. Math. 176 (1936), 31–44.Google Scholar