Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gamboa, F.
and
Gassiat, E.
1996.
Sets of Superresolution and the Maximum Entropy Method on the Mean.
SIAM Journal on Mathematical Analysis,
Vol. 27,
Issue. 4,
p.
1129.
Gamboa, F.
and
Gzyl, H.
1997.
Solving Fredholm equations by maximum entropy on the mean. application to superresolution.
Mathematical and Computer Modelling,
Vol. 25,
Issue. 7,
p.
23.
Gamboa, F.
and
Gassiat, E.
1997.
Bayesian methods and maximum entropy for ill-posed inverse problems.
The Annals of Statistics,
Vol. 25,
Issue. 1,
Gamboa, Fabrice
and
Lozada-Chang, Li-Vang
2004.
Large Deviations for random power moment problem.
The Annals of Probability,
Vol. 32,
Issue. 3B,
de Castro, Yohann
and
Gamboa, Fabrice
2012.
Exact reconstruction using Beurling minimal extrapolation.
Journal of Mathematical Analysis and Applications,
Vol. 395,
Issue. 1,
p.
336.
Azaïs, Jean-Marc
de Castro, Yohann
and
Gamboa, Fabrice
2015.
Spike detection from inaccurate samplings.
Applied and Computational Harmonic Analysis,
Vol. 38,
Issue. 2,
p.
177.
Matei, Basarab
2015.
Exact reconstruction of a class of nonnegative measures using model sets.
p.
578.
Matei, Basarab
2016.
Exact reconstruction of the nonnegative measures using model sets.
Asymptotic Analysis,
Vol. 97,
Issue. 3-4,
p.
291.
De Castro, Yohann
Gamboa, F.
Henrion, Didier
and
Lasserre, J.-B.
2017.
Exact Solutions to Super Resolution on Semi-Algebraic Domains in Higher Dimensions.
IEEE Transactions on Information Theory,
Vol. 63,
Issue. 1,
p.
621.
Eftekhari, Armin
Tanner, Jared
Thompson, Andrew
Toader, Bogdan
and
Tyagi, Hemant
2021.
Sparse non-negative super-resolution — simplified and stabilised.
Applied and Computational Harmonic Analysis,
Vol. 50,
Issue. ,
p.
216.
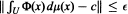 is almost concentrated on Rα,δ(∊). When Ф is a pointwise T-system (extension of T-systems), the study of the set Rα,δ(∊) leads to the evaluation of the Prokhorov radius of the set
is almost concentrated on Rα,δ(∊). When Ф is a pointwise T-system (extension of T-systems), the study of the set Rα,δ(∊) leads to the evaluation of the Prokhorov radius of the set 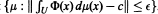 .
.



