Article contents
A Special Case of Completion Invariance for the c2 Invariant of a Graph
Published online by Cambridge University Press: 20 November 2018
Abstract
The 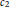 ${{c}_{2}}$ invariant is an arithmetic graph invariant defined by Schnetz. It is useful for understanding Feynman periods. Brown and Schnetz conjectured that the
${{c}_{2}}$ invariant is an arithmetic graph invariant defined by Schnetz. It is useful for understanding Feynman periods. Brown and Schnetz conjectured that the 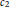 ${{c}_{2}}$ invariant has a particular symmetry known as completion invariance. This paper will prove completion invariance of the
${{c}_{2}}$ invariant has a particular symmetry known as completion invariance. This paper will prove completion invariance of the 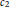 ${{c}_{2}}$ invariant in the case where we are over the field with 2 elements and the completed graph has an odd number of vertices. The methods involve enumerating certain edge bipartitions of graphs; two different constructions are needed.
${{c}_{2}}$ invariant in the case where we are over the field with 2 elements and the completed graph has an odd number of vertices. The methods involve enumerating certain edge bipartitions of graphs; two different constructions are needed.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2018
References
- 2
- Cited by


