Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-25T17:27:00.802Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Results on the Schroeder–Bernstein Property for Separable Banach Spaces

Published online by Cambridge University Press:  20 November 2018

Valentin Ferenczi  and
Elόi Medina Galego
Valentin Ferenczi
Affiliation:
Institut de Mathématiques de Jussieu, Projet Analyse Fonctionnelle, Université Pierre et Marie Curie – Paris 6, Boîte 186, 4, Place Jussieu 75252, Paris Cedex 05, France e-mail: ferenczi@ccr.jussieu.fr
Elόi Medina Galego
Affiliation:
Department of Mathematics, IME, University of São Paulo, São Paulo 05315-970, Brazil e-mail: eloi@ime.usp.br, ferenczi@ime.usp.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct a continuum of mutually non-isomorphic separable Banach spaces which are complemented in each other. Consequently, the Schroeder–Bernstein Index of any of these spaces is 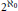${{2}^{{\aleph_{0}}}}$. Our construction is based on a Banach space introduced by W. T. Gowers and B. Maurey in 1997. We also use classical descriptive set theory methods, as in some work of the first author and C. Rosendal, to improve some results of P. G. Casazza and of N. J. Kalton on the Schroeder–Bernstein Property for spaces with an unconditional finite-dimensional Schauder decomposition.

Keywords

46B0346B20complemented subspacesSchroeder–Bernstein property
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 1 , 01 February 2007 , pp. 63 - 84
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Casazza, P. G., Finite dimensional decompositions in Banach spaces. In: Geometry of Normed Linear Spaces. Contemp. Math. 52, American Mathematical Society, Providence, RI, 1986, pp. 1–29.Google Scholar
[2] Casazza, P. G., The Schroeder-Bernstein property for Banach space. In: Banach Space Theory. Contemp. Math. 85, American Mathematical Society, Providence, RI, 1989, pp. 61–77.Google Scholar
[3] Castillo, J. M. F. and González, M., Three-Space Problems in Banach Spaces Theory. Lecture Notes in Mathematics 1667, Springer-Verlag, Berlin, 1997.Google Scholar
[4] Ferenczi, V., A uniformly convex and hereditarily indecomposable Banach space. Israel J. Math. 102(1997), 199–225.Google Scholar
[5] Ferenczi, V. and Galego, E. M., Some equivalence relations which are Borel reducible to isomorphism between Banach spaces. Israel J. Math. 152(2006), 61–82.Google Scholar
[6] Ferenczi, V. and Rosendal, C., On the number of non-isomorphic subspaces of a Banach space. Studia Math. 168(2005), no. 3, 203–216.Google Scholar
[7] Ferenczi, V. and Rosendal, C., Ergodic Banach spaces. Adv. Math. 195(2005), no. 1, 259–282.Google Scholar
[8] Galego, E. M., On solutions to the Schroeder-Bernstein problem for Banach spaces. Arch. Math. (Basel) 79(2002), no. 4, 299–307.Google Scholar
[9] Galego, E. M., The Schroeder-Bernstein index for Banach spaces. Studia Math. 164(2004), no. 1, 29–38.Google Scholar
[10] Gasparis, I., A continuum of totally incomparable hereditarily indecomposable Banach spaces. Studia Math. 151(2002), no. 3, 277–298.Google Scholar
[11] Gowers, W. T., A solution to the Schroeder-Bernstein problem for Banach spaces. Bull. London Math. Soc. 28(1996), no. 3, 297–304.Google Scholar
[12] Gowers, W. T. and Maurey, B., The unconditional basic sequence problem. J. Amer. Math. Soc. 6(1993), no. 4, 851–874.Google Scholar
[13] Gowers, W. T. and Maurey, B., Banach spaces with small spaces of operators. Math. Ann. 307(1997), no. 4, 543–568.Google Scholar
[14] Herman, R. and Whitley, R., An example concerning reflexivity. Studia Math. 28(1966/67) 289–294.Google Scholar
[15] Kalton, N. J., A remark on Banach spaces isomorphic to their squares. In: Function Spaces. Contemp. Math. 232, American Mathematical Society, Providence, RI, 1999, pp. 211–217.Google Scholar
[16] Kechris, A. S.. Classical Descriptive Set Theory. Graduate Texts in Mathematics 156, Springer-Verlag, New York, 1995.Google Scholar
[17] Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. I. Sequence Spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete 92, Springer-Verlag, New York. 1979.Google Scholar
[18] Rosendal, C., Incomparable, non isomorphic and minimal Banach spaces. Fund. Math. 183(2004), no. 3, 253–274.Google Scholar
[19] Schlumprecht, T., An arbitrarily distortable Banach space. Israel J. Math. 76(1991), no. 1-2, 81–95.Google Scholar
[20] Wojtaszczyk, P., On projections and unconditional bases in direct sums of Banach spaces. II. Studia Math. 62(1978), no. 2, 193–201.Google Scholar