Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Della Dora, J.
and
Richard-Jung, F.
2000.
Computer Algebra in Scientific Computing.
p.
113.
Beringer, Frédéric
and
Richard-Jung, Françoise
2003.
Symbolic and Numerical Scientific Computation.
Vol. 2630,
Issue. ,
p.
240.
Aroca, Fuensanta
2004.
Puiseux parametric equations of analytic sets.
Proceedings of the American Mathematical Society,
Vol. 132,
Issue. 10,
p.
3035.
Aroca, Fuensanta
2007.
Real and Complex Singularities.
p.
15.
Aroca, Fuensanta
and
Ilardi, Giovanna
2009.
A Family of Algebraically Closed Fields Containing Polynomials in Several Variables.
Communications in Algebra,
Vol. 37,
Issue. 4,
p.
1284.
Sasaki, Tateaki
and
Inaba, Daiju
2009.
Convergence and many-valuedness of hensel seriesnear the expansion point.
p.
159.
AROCA, FUENSANTA
ILARDI, GIOVANNA
and
LÓPEZ DE MEDRANO, LUCÍA
2010.
PUISEUX POWER SERIES SOLUTIONS FOR SYSTEMS OF EQUATIONS.
International Journal of Mathematics,
Vol. 21,
Issue. 11,
p.
1439.
Esterov, A.
2010.
Newton Polyhedra of Discriminants of Projections.
Discrete & Computational Geometry,
Vol. 44,
Issue. 1,
p.
96.
Perez, P. D. G.
2010.
Bijectiveness of the Nash Map for Quasi-Ordinary Hypersurface Singularities.
International Mathematics Research Notices,
Soto, M.J.
and
Vicente, J.L.
2011.
The Newton Procedure for several variables.
Linear Algebra and its Applications,
Vol. 435,
Issue. 2,
p.
255.
Sasaki, Tateaki
and
Inaba, Daiju
2012.
A study of Hensel series in general case.
p.
34.
Parusiński, Adam
and
Rond, Guillaume
2012.
The Abhyankar–Jung Theorem.
Journal of Algebra,
Vol. 365,
Issue. ,
p.
29.
Sasaki, Tateaki
and
Inaba, Daiju
2014.
Computer Mathematics.
p.
125.
González Villa, Manuel
2014.
Newton process and semigroups of irreducible quasi-ordinary power series.
Revista de la Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matematicas,
Vol. 108,
Issue. 1,
p.
259.
Saavedra, Víctor M.
2017.
The McDonald theorem in positive characteristic.
Journal of Algebra,
Vol. 491,
Issue. ,
p.
219.
García Barroso, Evelia Rosa
González Pérez, Pedro Daniel
and
Popescu-Pampu, Patrick
2017.
Variations on inversion theorems for Newton–Puiseux series.
Mathematische Annalen,
Vol. 368,
Issue. 3-4,
p.
1359.
Hickel, Michel
and
Matusinski, Mickaël
2019.
About algebraic Puiseux series in several variables.
Journal of Algebra,
Vol. 527,
Issue. ,
p.
55.
Aroca, Fuensanta
and
Rond, Guillaume
2019.
Support of Laurent series algebraic over the field of formal power series.
Proceedings of the London Mathematical Society,
Vol. 118,
Issue. 3,
p.
577.
Belotto da Silva, André
Curmi, Octave
and
Rond, Guillaume
2021.
A proof of A. Gabrielov’s rank theorem.
Journal de l’École polytechnique — Mathématiques,
Vol. 8,
Issue. ,
p.
1329.
Aroca, Fuensanta
Decaup, Julie
and
Rond, Guillaume
2022.
The minimal cone of an algebraic Laurent series.
Mathematische Annalen,
Vol. 382,
Issue. 3-4,
p.
1745.
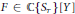 $F\,\in \,\mathbb{C}\,\{{{S}_{\mathcal{T}}}\}\,\left[ Y \right]$ à coefficients dans l’anneau de germes de fonctions holomorphes au point spécial d’une variété torique affine. Nous généralisons à ce cas la paramétrisation classique des singularités quasi-ordinaires. Cela fait intervenir d’une part une généralization de l’algorithme de Newton-Puiseux, et d’autre part une relation entre le polyèdre de Newton du discriminant de
$F\,\in \,\mathbb{C}\,\{{{S}_{\mathcal{T}}}\}\,\left[ Y \right]$ à coefficients dans l’anneau de germes de fonctions holomorphes au point spécial d’une variété torique affine. Nous généralisons à ce cas la paramétrisation classique des singularités quasi-ordinaires. Cela fait intervenir d’une part une généralization de l’algorithme de Newton-Puiseux, et d’autre part une relation entre le polyèdre de Newton du discriminant de  $F$ par rapport à
$F$ par rapport à  $Y$ et celui de
$Y$ et celui de  $F$ au moyen du polytope-fibre de Billera et Sturmfels. Cela nous permet enfin de calculer, sous des hypothèses de non dégénérescence, les sommets du polyèdre de Newton du discriminant a partir de celui de
$F$ au moyen du polytope-fibre de Billera et Sturmfels. Cela nous permet enfin de calculer, sous des hypothèses de non dégénérescence, les sommets du polyèdre de Newton du discriminant a partir de celui de  $F$, et les coefficients correspondants à partir des coefficients des exposants de
$F$, et les coefficients correspondants à partir des coefficients des exposants de  $F$ qui sont dans les arêtes de son polyèdre de Newton.
$F$ qui sont dans les arêtes de son polyèdre de Newton.

