Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-23T12:56:22.579Z Has data issue: false hasContentIssue false
  • English
  • Français

Random Dirichlet Functions: Multipliers and Smoothness

Published online by Cambridge University Press:  20 November 2018

W. George Cochran ,
Joel H. Shapiro  and
David C. Ullrich
W. George Cochran
Affiliation:
Louisiana State University, Baton Rouge, Louisiana 70803, U.S.A., Email: cochran@mmdehn.dnet.lsu.edu
Joel H. Shapiro
Affiliation:
Michigan State University, East Lansing, Michigan 48824, U.S.A., Email: 21144jhs@msu.bitnet
David C. Ullrich
Affiliation:
Oklahoma State University, Stillwater, Oklahoma 74078, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if 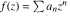is a holomorphic function in the Dirichlet space of the unit disk, then almost all of its randomizations 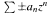are multipliers of that space. This parallels a known result for lacunary power series, which also has a version for smoothness classes: every lacunary Dirichlet series lies in the Lipschitz class Lip1/2 of functions obeying a Lipschitz condition with exponent 1/2. However, unlike the lacunary situation, no corresponding “almost sure” Lipschitz result is possible for random series: we exhibit a Dirichlet function with norandomization in Lip1/2. We complement this result with a “best possible” sufficient condition for randomizations to belong almost surely to Lip1/2. Versions of our results hold for weighted Dirichlet spaces, and much of our work is carried out in this more general setting.

Keywords

30B2047B38
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 45 , Issue 2 , 01 April 1993 , pp. 255 - 268
Copyright
Copyright © Canadian Mathematical Society 1993

References

1. Anderson, J.M., Clunie, J.G. and Pommerenke, Ch., On Block Functions and Normal Functions, J. Reine Angew. Math. 270(1974), 12–37.Google Scholar
2. S. Bourdon, P. and Shapiro, J.H., Spectral synthesis and common cyclic vectors, Michigan Math. J. 37(1990), 71–90.Google Scholar
3. Brown, L. and Shields, A.L., Cyclic vectors in the Dirichlet space, Trans. Amer. Math. Soc. 285(1984), 269–304.Google Scholar
4. Duren, P.L., Theory of Hp Spaces, Academic Press, 1970.Google Scholar
5. Duren, P.L., Random series and bounded mean oscillation, Michigan Math. J. 32(1985), 81 -86.Google Scholar
6. Duren, P.L., Romberg, B.R. and Shields, A.L., Linear Junctionals on Hp spaces with 0 < p < 1, J. Reine Angew. Math. 238(1969), 32–60.Google Scholar
7. Godefroy, G. and Shapiro, J.H., Operators with dense, invariant, cyclic vector manifolds, J. Functional Analysis 98(1991), 229–269.Google Scholar
8. Kahane, J.P. Some random series of functions, 2nd éd., Cambridge Univ. Press, 1985.Google Scholar
9. Kerman, R. and Sawyer, E., Carleson measures and multipliers of Dirichlet-type spaces, Trans. Amer. Math. Soc. 309(1988), 87–98.Google Scholar
10. Salem, R. and Zygmund, A., Some properties of trigonometric series whose terms have random signs, Acta Math. 91(1954), 244–301.Google Scholar
11. Shields, A.L., Weighted shift operators and analytic function theory, In: Mathematical Surveys, 13, (ed. Pearcy, C.), Amer. Math. Society, 1974.Google Scholar
12. Shields, A.L. and Wallen, L.J., The commutants of certain Hilbert space operators, Indiana Univ. Math. J. 20(1971), 777–788.Google Scholar
13. Sledd, W.T., Random series which are BMO or Bloch, Michigan Math. Jour. 28(1981), 259–266.Google Scholar
14. Stegenga, D.A., Multipliers of the Dirichlet space, Illinois J. Math. 24(1980), 113–139.Google Scholar
15. Taylor, G.D., Multipliers on Dα, Trans. Amer. Math. Soc. 123(1966), 229–240.Google Scholar
16. Zygmund, A., Trigonometric Series, I, 2nd ed. Cambridge Univ. Press, 1959.Google Scholar