Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T10:33:33.766Z Has data issue: false hasContentIssue false
  • English
  • Français

PDE comparison principles for Robin problems

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  23 September 2021

Jeffrey J. Langford
Jeffrey J. Langford*
Affiliation:
Department of Mathematics, Bucknell University, Lewisburg, PA, USA
*
e-mail: jeffrey.langford@bucknell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We compare the solutions of two Poisson problems in a spherical shell with Robin boundary conditions, one with given data, and one where the data have been cap symmetrized. When the Robin parameters are nonnegative, we show that the solution to the symmetrized problem has larger convex means. Sending one of the Robin parameters to 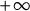$+\infty $ , we obtain mixed Robin/Dirichlet comparison results in shells. We prove similar results on balls and prove a comparison principle on generalized cylinders with mixed Robin/Neumann boundary conditions.

Keywords

Symmetrizationcomparison theoremsPoisson’s equationRobin boundary conditions

MSC classification

Primary: 35J05: Laplacian operator, reduced wave equation (Helmholtz equation), Poisson equation 35B51: Comparison principles
Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 1 , February 2023 , pp. 108 - 139
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alvino, A., Chiacchio, F., Nitsch, C., and Trombetti, C., Sharp estimates for solutions to elliptic problems with mixed boundary conditions. J. Math. Pures App. 152(2021), no. 9, 251–261.Google Scholar
Alvino, A., Diaz, J. I., Lions, P. L., and Trombetti, G., Elliptic equations and Steiner symmetrization . Comm. Pure Appl. Math. 49(1996), no. 3, 217–236.10.1002/(SICI)1097-0312(199603)49:3<217::AID-CPA1>3.0.CO;2-G3.0.CO;2-G>CrossRefGoogle Scholar
Alvino, A., Nitsch, C., and Trombetti, C., A Talenti comparison result for solutions to elliptic problems with Robin boundary conditions. Preprint, 2020. arXiv:1909.11950 Google Scholar
Antunes, P. R. S., Freitas, P., and Krejčiřík, D., Bounds and extremal domains for Robin eigenvalues with negative boundary parameter . Adv. Calc. Var. 10(2017), 357–379.CrossRefGoogle Scholar
Baernstein, A. II, Proof of Edrei’s spread conjecture . Proc. Lond. Math. Soc. 26(1973), no. 3, 418–434.10.1112/plms/s3-26.3.418CrossRefGoogle Scholar
Baernstein, A. II, Integral means, univalent functions and circular symmetrization . Acta Math. 133(1974), 139–169.10.1007/BF02392144CrossRefGoogle Scholar
Baernstein, A. II, How the *-function solves extremal problems . In: Proceedings of the international congress of mathematicians (Helsinki, 1978), Academiæ Scientiarum Fennicæ, Helsinki, 1980, pp. 639–644.Google Scholar
Baernstein, A. II, A unified approach to symmetrization . In: Alvino, A., Fabes, E., and Talenti, G. (eds.), Partial differential equations of elliptic type (Cortona, 1992), Symposium Mathematics, XXXV, Cambridge University Press, Cambridge, 1994, pp. 47–91.Google Scholar
Baernstein, A. II, The *-function in complex analysis . In: Koehnau, R. (ed.), Handbook of complex analysis, vol. I: geometric function theory, Elsevier Science, North-Holland, Amsterdam, 2002, pp. 229–271.Google Scholar
Baernstein, A. II, Symmetrization in analysis, New Mathematical Monographs, 36, Cambridge University Press, Cambridge, 2019, xviii + 473 pp. With David Drasin and Richard S. Laugesen.10.1017/9781139020244CrossRefGoogle Scholar
Bareket, M., On an isoperimetric inequality for the first eigenvalue of a boundary value problem . SIAM J. Math. Anal. 8(1977), 280–287.CrossRefGoogle Scholar
Bers, L. and Nirenberg, L., On linear and non-linear elliptic boundary value problems in the plane . In: Convegno internazionale sulle equazioni lineari alle derivate parziali (Trieste, 1954), Edizioni Cremonese, Roma, 1955, pp. 141–167.Google Scholar
Bossel, M.-H., Membranes élastiquement liées: extension du théoréme de Rayleigh–Faber–Krahn et de l’inégalité de Cheeger . C. R. Acad. Sci. Paris Sér. I Math. 302(1986), 47–50.Google Scholar
Brock, F., Steiner symmetrization and periodic solutions of boundary value problems . Z. Anal. Anwend. 13(1994), no. 3, 417–423.CrossRefGoogle Scholar
Bucur, D., Ferone, V., Nitsch, C., and Trombetti, C., A sharp estimate for the first Robin–Laplacian eigenvalue with negative boundary parameter. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 30(2019), no. 4, 665–676.Google Scholar
Bucur, D. and Giacomini, A., A variational approach to the isoperimetric inequality for the Robin eigenvalue problem . Arch. Ration. Mech. Anal. 198(2010), 927–961.10.1007/s00205-010-0298-6CrossRefGoogle Scholar
Bucur, D. and Giacomini, A., Faber–Krahn inequalities for the Robin–Laplacian: a free discontinuity approach . Arch. Ration. Mech. Anal. 218(2015), 757–824.CrossRefGoogle Scholar
Chasman, L. M. and Langford, J. J., A sharp isoperimetric inequality for the second eigenvalue of the Robin plate. To appear in Journal of Spectral Theory.Google Scholar
Daners, D., A Faber–Krahn inequality for Robin problems in any space dimension . Math. Ann. 335(2006), 767–785.CrossRefGoogle Scholar
Evans, L. C. and Gariepy, R. F., Measure theory and fine properties of functions, Studies in Advanced Mathematics, CRC Press, Boca Raton, FL, 1992, viii + 268 pp.Google Scholar
Freitas, P. and Krejčiřík, D., The first Robin eigenvalue with negative boundary parameter . Adv. Math. 280(2015), 322–339.10.1016/j.aim.2015.04.023CrossRefGoogle Scholar
Freitas, P. and Laugesen, R. S., From Steklov to Neumann and beyond, via Robin: the Szegő way . Canad. J. Math. 72(2019), no. 4, 1024–1043.Google Scholar
Freitas, P. and Laugesen, R. S., From Neumann to Steklov and beyond, via Robin: the Weinberger way. Amer. J. Math, 143(2021), no. 3, 969–994.Google Scholar
Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order, Classics in Mathematics, 224, Springer, Berlin, 2001, reprint of the 1998 edition.CrossRefGoogle Scholar
Girouard, A. and Laugesen, R. S., Robin spectrum: two disks maximize the third eigenvalue. Indiana Univ. Math. J., to appear.Google Scholar
Kawohl, B., Rearrangements and convexity of level sets in PDE, Lecture Notes in Mathematics, 1150, Springer, Berlin, 1985.Google Scholar
Ladyzenskaja, O. A. and Ural’ceva, N. N., Linear and quasilinear elliptic equations, Academic Press, New York–London, 1968.Google Scholar
Langford, J. J., Comparison theorems in elliptic partial differential equations with Neumann boundary conditions. Ph.D. thesis, Washington University in St. Louis, 2012.Google Scholar
Langford, J. J., Symmetrization of Poisson’s equation with Neumann boundary conditions . Ann. Sc. Norm. Super. Pisa Cl. Sci. 14(2015), no. 4, 1025–1063.Google Scholar
Langford, J. J., Neumann comparison theorems in elliptic PDEs . Potential Anal. 43(2015), no. 3, 415–459.Google Scholar
Langford, J. J., Subharmonicity, comparison results, and temperature gaps in cylindrical domains . Differential Integral Equations 29(2016), nos. 5–6, 493–512.CrossRefGoogle Scholar
Lieb, E. H. and Loss, M., Analysis. 2nd ed., Graduate Studies in Mathematics, 14, American Mathematical Society, Providence, RI, 2001.Google Scholar
Littman, W., A strong maximum principle for weakly L-subharmonic functions . J. Math. Mech. 8(1959), 761–770.Google Scholar
Nardi, G., Schauder estimate for solutions of Poisson’s equation with Neumann boundary conditions . Enseign. Math. 60(2014), nos. 3–4, 421–435.CrossRefGoogle Scholar
Sarvas, J., Symmetrization of condensers in n-space . Ann. Acad. Sci. Fenn. Ser. A. 522(1972), 44.Google Scholar
Talenti, G., Elliptic equations and rearrangements . Ann. Sc. Norm. Super. Pisa Cl. Sci. 3(1976), no. 4, 697–718.Google Scholar
Talenti, G., The art of rearranging . Milan J. Math. 84(2016), no. 1, 105–157.CrossRefGoogle Scholar
Weitsman, A., Spherical symmetrization in the theory of elliptic partial differential equations . Comm. Partial Differential Equations 8(1983), no. 5, 545–561.CrossRefGoogle Scholar