Hostname: page-component-7479d7b7d-t6hkb Total loading time: 0 Render date: 2024-07-13T17:31:48.508Z Has data issue: false hasContentIssue false
  • English
  • Français

On Weakly Tight Families

Published online by Cambridge University Press:  20 November 2018

Dilip Raghavan  and
Juris Steprāns
Dilip Raghavan
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4 email: raghavan@math.toronto.edu
Juris Steprāns
Affiliation:
Department of Mathematics, York University, Toronto, ON M3J 1P3 email: steprans@yorku.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using ideas from Shelah's recent proof that a completely separable maximal almost disjoint family exists when 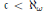$c<{{\aleph }_{\omega }}$, we construct a weakly tight family under the hypothesis 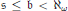$\mathfrak{s}\le \mathfrak{b}<{{\aleph }_{\omega }}$. The case when 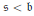$\mathfrak{s}<\mathfrak{b}$ is handled in ZFC and does not require 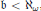$\mathfrak{b}<{{\aleph }_{\omega }}$, while an additional PCF type hypothesis, which holds when 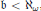$\mathfrak{b}<{{\aleph }_{\omega }}$ is used to treat the case 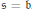$\mathfrak{s}=\mathfrak{b}$. The notion of a weakly tight family is a natural weakening of the well-studied notion of a Cohen indestructible maximal almost disjoint family. It was introduced by Hrušák and García Ferreira [8], who applied it to the Katétov order on almost disjoint families.

Keywords

03E1703E1503E3503E4003E0503E5003E65maximal almost disjoint familycardinal invariants
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 6 , 01 December 2012 , pp. 1378 - 1394
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Balcar, B., J. Dočkálková, and Simon, P., Almost disjoint families of countable sets. In: Finite and infinite sets, Vols. I, II (Eger, 1981), Colloq. Math. Soc. János Bolyai 37, North-Holland, Amsterdam, 1984, 59–88.Google Scholar
[2] Balcar, B. and Simon, P., Disjoint refinement. In: Handbook of Boolean algebras, Vol. 2, North-Holland, Amsterdam, 1989, 333–388.Google Scholar
[3] Brendle, J., Mob families and mad families. Arch. Math. Logic 37(1997), 183–197. http://dx.doi.org/10.1007/s001530050091 Google Scholar
[4] Brendle, J. and Yatabe, S., Forcing indestructibility of MAD families. Ann. Pure Appl. Logic 132(2005), 271–312. http://dx.doi.org/10.1016/j.apal.2004.09.002 Google Scholar
[5] Erdʺos, P. and Shelah, S., Separability properties of almost-disjoint families of sets. Israel J. Math. 12(1972), 207–214. http://dx.doi.org/10.1007/BF02764666 Google Scholar
[6] Fuchino, S., Koppelberg, S., and Shelah, S., Partial orderings with the weak Freese–Nation property. Ann. Pure Appl. Logic 80(1996), 35–54. http://dx.doi.org/10.1016/0168-0072(95)00047-X Google Scholar
[7] Hrušák, M., MAD families and the rationals. Comment. Math. Univ. Carolin. 42(2001), 345–352.Google Scholar
[8] Hrušák, M. and S. Garcıa Ferreira, Ordering MAD families a la Katétov. J. Symbolic Logic 68(2003), 1337–1353. http://dx.doi.org/10.2178/jsl/1067620190 Google Scholar
[9] Kurilic, M. S., Cohen-stable families of subsets of integers. J. Symbolic Logic 66(2001), 257–270. http://dx.doi.org/10.2307/2694920 Google Scholar
[10] Larson, P. B., Almost-disjoint coding and strongly saturated ideals. Proc. Amer. Math. Soc. 133(2005), 2737–2739. http://dx.doi.org/10.1090/S0002-9939-05-07824-X Google Scholar
[11] Malykhin, V. I., Topological properties of Cohen generic extensions. Trudy Moskov. Mat. Obshch. 52(1989), 3–33, 247.Google Scholar
[12] Miller, A. W., Arnie Miller's problem list. In: Set theory of the reals (Ramat Gan, 1991), Israel Math. Conf. Proc. 6, Bar-Ilan Univ., Ramat Gan, 1993, 645–654.Google Scholar
[13] Mrówka, S., On completely regular spaces. Fund. Math. 41(1954), 105–106.Google Scholar
[14] Mró;wka, S., Some set-theoretic constructions in topology. Fund. Math. 94(1977), 83–92.Google Scholar
[15] Raghavan, D., Maximal almost disjoint families of functions. Fund. Math. 204(2009), 241–282. http://dx.doi.org/10.4064/fm204-3-3 Google Scholar
[16] Raghavan, D., Almost disjoint families and diagonalizations of length continuum. Bull. Symbolic Logic 16(2010), 240–260. http://dx.doi.org/10.2178/bsl/1286889125 Google Scholar
[17] Raghavan, D., There is a Van Douwen MAD family. Trans. Amer. Math. Soc. 362(2010), 5879–5891. http://dx.doi.org/10.1090/S0002-9947-2010-04975-X Google Scholar
[18] Shelah, S., Mad families and sane player. Canad. J. Math. 63(2011), 1416-1436. http://dx.doi.org/10.4153/CJM-2011-057-1 Google Scholar
[19] Shelah, S., On cardinal invariants of the continuum. In: Axiomatic set theory (Boulder, Colo., 1983), Contemp. Math. 31, Amer. Math. Soc., Providence, RI, 1984, 183–207.Google Scholar
[20] Simon, P., A note on almost disjoint refinement. Acta Univ. Carolin. Math. Phys. 37(1996), 89–99.Google Scholar