Article contents
On Group Rings
Published online by Cambridge University Press: 20 November 2018
Extract
Let R be a commutative ring with unity and let G be a group. The group ring RG is a free R-module having the elements of G as a basis, with multiplication induced by
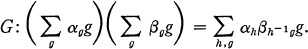
The first theorem in this paper deals with idempotents in RG and improves a result of Connell. In the second section we consider the Jacobson radical of RG, and we prove a theorem about a class of algebras that includes RG when G is locally finite and R is an algebraically closed field of characteristic zero. The last theorem shows that if R is a field and G is a finite nilpotent group, then RG determines RP for every Sylow subgroup P of G, regardless of the characteristic of R.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1970
References
- 3
- Cited by


