Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T22:19:04.629Z Has data issue: false hasContentIssue false
  • English
  • Français

On Absolute Summability by Riesz and Generalized Cesàro Means. II

Published online by Cambridge University Press:  20 November 2018

H.-H. Körle
H.-H. Körle*
Affiliation:
Universität Marburg, Marburg, Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. We will use the terminology of part I [9], including the general assumptions of [9, § 1]. In that paper we had proved that |R, λ, κ| = |C, λ, κ| in case that κ is an integer. Now, we turn to non-integral orders κ.

As to ordinary summation, the following inclusion relations (in the customary sense; see [9, end of § 1]) for non-integral κ have been established so far. (Since we are comparing Riesz methods of the same type λ and order κ only, (R, λ, κ) is written (R), etc., for the moment.) (R) ⊆ (C) is a result by Borwein and Russell [2]. (C) ⊆ (R) was proved by Jurkat [3] in the case 0 < κ < 1, and, after Borwein [1], it holds in the case 1 < κ < 2 if

(1)

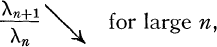
(2)

(i.e. decreases in the wide sense).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 2 , 01 April 1970 , pp. 209 - 218
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Borwein, D., On generalized Cesaro summability, Indian J. Math. 9 (1967), 55–64.Google Scholar
2. Borwein, D. and Russell, D. C., On Riesz and generalised Cesàro summability of arbitrary positive order, Math. Z. 99 (1967), 171–177.Google Scholar
3. Jurkat, W., Über Rieszsche Mittel mit unstetigem Parameter, Math. Z. 55 (1951), 8–12.Google Scholar
4. H.-H., Körle, Über unstetige absolute Riesz-Summierung. I, Math. Ann. 176 (1968), 45–52.Google Scholar
5. H.-H., Körle, Über unstetige absolute Riesz-Summierung. II, Math. Ann. 177 (1968), 230–234.Google Scholar
6. H.-H., Körle, Qn the equivalence of continuous and the discontinuous absolute Riesz means. I, Indian J. Math. 11 (1969), 11–16.Google Scholar
7. H.-H., Körle, On the equivalence of continuous and the discontinuous absolute Riesz means. II, Indian J. Math. 11 (1969), 83–90.Google Scholar
8. H.-H., Körle, A Tauberian theorem for the discontinuous absolute Riesz means, Indian J. Math. 12 (1970), 13–20.Google Scholar
9. H.-H., Körle, On absolute summability by Riesz and generalized Cesàro means. I, Can. J. Math. 22 (1970), 202–208.Google Scholar
10. Norlund, N. E., Vorlesungen Über Differenzenrechnung (Springer, Berlin, 1924).Google Scholar
11. Peyerimhoff, A., On discontinuous Riesz means, Indian J. Math. 6 (1964), 69–91.Google Scholar
12. Wilansky, A. and Zeller, K., Abschnittsbeschrdnkte Matrixtransformationen; starke Limitierbarkeit, Math. Z. 64 (1956), 258–269.Google Scholar