Article contents
Non-tame Mice from Tame Failures of the Unique Branch Hypothesis
Published online by Cambridge University Press: 20 November 2018
Abstract
In this paper, we show that the failure of the unique branch hypothesis 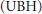 $\left( \text{UBH} \right)$ for tame trees implies that in some homogenous generic extension of
$\left( \text{UBH} \right)$ for tame trees implies that in some homogenous generic extension of 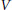 $V$ there is a transitive model
$V$ there is a transitive model 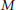 $M$ containing Ord
$M$ containing Ord 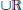 $\cup \mathbb{R}$ such that
$\cup \mathbb{R}$ such that 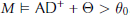 $M\,\vDash \,\text{A}{{\text{D}}^{+}}\,+\,\Theta \,>\,{{\theta }_{0}}$. In particular, this implies the existence (in
$M\,\vDash \,\text{A}{{\text{D}}^{+}}\,+\,\Theta \,>\,{{\theta }_{0}}$. In particular, this implies the existence (in 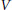 $V$) of a non-tame mouse. The results of this paper significantly extend J. R. Steel's earlier results for tame trees.
$V$) of a non-tame mouse. The results of this paper significantly extend J. R. Steel's earlier results for tame trees.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014
Footnotes
The first author's work was supported by NSF Grant No DMS-1201348.
References
- 2
- Cited by


