Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Martindale, W.S
and
Miers, C.Robert
1992.
Generalized Lie ideals in ★-prime rings.
Journal of Algebra,
Vol. 152,
Issue. 1,
p.
94.
Brşr, Matej
Martindale, W.S.
and
Robert Miers, C.
1993.
On some identities in prime rings with involution.
Communications in Algebra,
Vol. 21,
Issue. 12,
p.
4679.
Smirnov, Oleg N.
1999.
Finite Z-Gradings of Lie Algebras and Symplectic Involutions.
Journal of Algebra,
Vol. 218,
Issue. 1,
p.
246.
Gómez-Ambrosi, Carlos
Laliena, Jesús
and
Shestakov, Ivan P.
2000.
On the lie structure of the skew elements of a prime superalgebra with superinvolution.
Communications in Algebra,
Vol. 28,
Issue. 7,
p.
3277.
Brešar, Matej
Eremita, Daniel
and
Wong, Tsai-Lien
2004.
On commutators and derivations in rings.
Journal of Algebra,
Vol. 278,
Issue. 2,
p.
704.
Brox, Jose
García, Esther
and
Gómez Lozano, Miguel
2016.
Jordan algebras at Jordan elements of semiprime rings with involution.
Journal of Algebra,
Vol. 468,
Issue. ,
p.
155.
Lee, Tsiu-Kwen
2018.
Ad-nilpotent Elements of Semiprime Rings with Involution.
Canadian Mathematical Bulletin,
Vol. 61,
Issue. 2,
p.
318.
Brox, Jose
García, Esther
Lozano, Miguel Gómez
Alcázar, Rubén Muñoz
and
de Salas, Guillermo Vera
2021.
A Description of Ad-nilpotent Elements in Semiprime Rings with Involution.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 44,
Issue. 4,
p.
2577.
Brox, Jose
García, Esther
Gómez Lozano, Miguel
Muñoz Alcázar, Rubén
and
Vera de Salas, Guillermo
2022.
Ad-Nilpotent Elements of Skew Index in Semiprime Rings with Involution.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 45,
Issue. 2,
p.
631.
García, Esther
Gómez Lozano, Miguel
and
Vera de Salas, Guillermo
2022.
Nilpotent superderivations in prime superalgebras.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 20,
p.
5547.
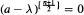 , (c) * is of the first kind, n ≡ 0 or n ≡ 3 (mod 4), and
, (c) * is of the first kind, n ≡ 0 or n ≡ 3 (mod 4), and 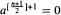 . Examples are given illustrating (c).
. Examples are given illustrating (c).

