Lushness, Numerical Index 1 and the Daugavet Property in Rearrangement Invariant Spaces

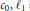We show that for spaces with 1–unconditional bases lushness, the alternative Daugavet property and numerical index 1 are equivalent. In the class of rearrangement invariant (r.i.) sequence spaces the only examples of spaces with these properties are ${{c}_{0,}}{{\ell }_{1}}$ and 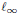${{\ell }_{\infty }}$ . The only lush r.i. separable function space on 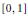$\left[ 0,1 \right]$ is 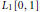${{L}_{1}}\left[ 0,1 \right]$ ; the same space is the only r.i. separable function space on 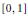$\left[ 0,1 \right]$ with the Daugavet property over the reals.

Keywords

46B04 46E30 lush space numerical index Daugavet property Köthe space rearrangement invariant space

Type

Research Article

Information

Canadian Journal of Mathematics , Volume 65 , Issue 2 , 01 April 2013 , pp. 331 - 348

DOI: https://doi.org/10.4153/CJM-2011-096-2

References

[1] Acosta, M. D., Kamińska, A. and Mastyło, M., The Daugavet property and weak neighborhoods in Banach lattices. J. Convex Analysis, to appear.Google Scholar

[2] Avilés, A., Kadets, V.,Martín, M., Merí, J. and Shepelska, V., Slicely countably determined Banach spaces. C. R. Math. Acad. Sci. Paris 347(2009), 1277–1280.Google Scholar

[3] Avilés, A., Slicely countably determined Banach spaces. Trans. Amer. Math. Soc. 362(2010), 4871–4900.Google Scholar

[4] Bennett, C. and Sharpley, R., Interpolation of Operators. Pure Appl. Math. 129, Academic Press, Inc., New York, 1988.Google Scholar

[5] Bourgain, J. and Rosenthal, H. P., Martingales valued in certain subspaces of L₁. Israel J. Math. 37(1980), 54–75. http://dx.doi.org/10.1007/BF02762868 Google Scholar

[6] Boyko, K., Kadets, V., Martín, M. and Werner, D., Numerical index of Banach spaces and duality. Math. Proc. Cambridge Philos Soc.. 142(2007), 93–102. http://dx.doi.org/10.1017/S0305004106009650 Google Scholar

[7] Duncan, J., McGregor, C., Pryce, J. and White, A., The numerical index of a normed space. J. London Math. Soc. 2(1970), 481–488.Google Scholar

[8] Ivakhno, Y. and Kadets, V., Unconditional sums of spaces with bad projections. Visn. Khark. Univ., Ser. Mat. Prykl. Mat. Mekh. 45 (2004), 30–35.Google Scholar

[9] Ivakhno, Y., Kadets, V. and Werner, D., The Daugavet property for spaces of Lipschitz functions. Math. Scand. 101(2007), 261–279; Corrigendum, Math. Scand. 104 (2009), 319.Google Scholar

[10] Kadets, V., Martín, M. and Merí, J., Norm equalities for operators on Banach spaces. Indiana Univ. Math. J. (2007), 2385–2411. http://dx.doi.org/10.1512/iumj.2007.56.3046 Google Scholar

[11] Kadets, V..Mart´ın, M., Merí, J., andPayá, R., Convexity and smoothness of Banach spaces with numerical index one. Illinois J. Math. 53(2009), 163–182.Google Scholar

[12] Kadets, V., Martín, M., Merí, J., and Shepelska, V., Lushness, numerical index one and duality. J. Math. Anal. Appl. 357(2009), 15–24. http://dx.doi.org/10.1016/j.jmaa.2009.03.055 Google Scholar

[13] Kadets, V., Shepelska, V. and Werner, D., Thickness of the unit sphere, ℓ1-types and the almost Daugavet property. Houston J. Math. 37(2011), 867–878.Google Scholar

[14] Kadets, V. and Shepelska, V., Sums of SCD sets and their applications to SCD operators and narrow operators. Cent. Eur. J. Math. 8(2010), 129–134. http://dx.doi.org/10.2478/s11533-009-0075-7 CrossRef Google Scholar

[15] Kadets, V. M., Shvidkoy, R. V., Sirotkin, G. G. and Werner, D., Banach spaces with the Daugavet property. Trans. Amer. Math. Soc. 352(2000), 855–873. http://dx.doi.org/10.1090/S0002-9947-99-02377-6 Google Scholar

[16] Kadets, V. and Werner, D., A Banach space with the Schur and the Daugavet property. Proc. Amer. Math. Soc. 132(2004), 1765–1773. http://dx.doi.org/10.1090/S0002-9939-03-07278-2 CrossRef Google Scholar

[17] Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces II. Springer-Verlag, Berlin-Heidelberg New York, 1979.CrossRef Google Scholar

[18] Lee, H. J., Martín, M. and Merí, J., Polynomial numerical indices of Banach spaces with absolute norm. Linear Algebra Appl. 435(2011), 400–408. http://dx.doi.org/10.1016/j.laa.2011.01.037 Google Scholar

[19] M. Martín, and Oikhberg, T., An alternative Daugavet property. J. Math. Anal. Appl. 294(2004), 158–180. http://dx.doi.org/10.1016/j.jmaa.2004.02.006 Google Scholar

[20] Okada, S.,Ricker, W. J. and Sánchez Pérez, E. A., Optimal Domain and Integral Extension of Operators Acting in Function Spaces. Oper. Theory Adv. Appl. 180, Birkhäuser Verlag, Basel, 2008.CrossRef Google Scholar

[21] Talagrand, M., The three-space problem for L₁. J. Amer. Math. Soc. 3(1990), 9–29.Google Scholar

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0

Total number of PDF views: 16 *

View data table for this chart

* Views captured on Cambridge Core between 20th November 2018 - 26th January 2021. This data will be updated every 24 hours.

Access

4 Cited by

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Lushness, Numerical Index 1 and the Daugavet Property in Rearrangement Invariant Spaces

Volume 65, Issue 2
Vladimir Kadets ^(a1), Miguel Martín ^(a2), Javier Merí ^(a2) and Dirk Werner ^(a3)
DOI: https://doi.org/10.4153/CJM-2011-096-2

Your Kindle email address

@free.kindle.com @kindle.com (service fees apply)

Available formats PDF

By using this service, you agree that you will only keep articles for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services.

Reply to: Submit a response

Title * Please enter a title for your response.

Contents * Please enter your response.

Your details

First name * Please enter your first name.

Last name * Please enter your last name.

Email * Please enter a valid email address.

Occupation Please enter your occupation.

Affiliation Please enter any affiliation.

Conflicting interests

Do you have any conflicting interests? *

Yes No

More information * Please enter details of the conflict of interest or select 'No'.

Please tick the box to confirm you agree to our Terms of use. *

Please accept terms of use.

Please tick the box to confirm you agree that your name, comment and conflicts of interest (if accepted) will be visible on the website and your comment may be printed in the journal at the Editor’s discretion. *

Please confirm you agree that your details will be displayed.

Article contents

Lushness, Numerical Index 1 and the Daugavet Property in Rearrangement Invariant Spaces

Abstract

Keywords

References

Full text views

Send article to Kindle

Send article to Dropbox

Send article to Google Drive

Reply to: Submit a response

Your details

Conflicting interests