No CrossRef data available.
Article contents
Lq Norms of Fekete and Related Polynomials
Published online by Cambridge University Press: 20 November 2018
Abstract
A Littlewood polynomial is a polynomial in 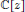 $\mathbb{C}\left[ z \right]$ having all of its coefficients in
$\mathbb{C}\left[ z \right]$ having all of its coefficients in 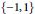 $\{-1,1\}$. There are various old unsolved problems, mostly due to Littlewood and Erdős, that ask for Littlewood polynomials that provide a good approximation to a function that is constant on the complex unit circle, and in particular have small
$\{-1,1\}$. There are various old unsolved problems, mostly due to Littlewood and Erdős, that ask for Littlewood polynomials that provide a good approximation to a function that is constant on the complex unit circle, and in particular have small  ${{L}^{q}}$ normon the complex unit circle. We consider the Fekete polynomials
${{L}^{q}}$ normon the complex unit circle. We consider the Fekete polynomials
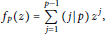 $${{f}_{p}}(z)=\sum\limits_{j=1}^{p-1}{(j|p){{z}^{j}}},$$
$${{f}_{p}}(z)=\sum\limits_{j=1}^{p-1}{(j|p){{z}^{j}}},$$
where  $p$ is an odd prime and
$p$ is an odd prime and 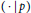 $(.|p)$ is the Legendre symbol (so that
$(.|p)$ is the Legendre symbol (so that 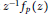 ${{z}^{-1}}{{f}_{p}}(z)$ is a Littlewood polynomial). We give explicit and recursive formulas for the limit of the ratio of
${{z}^{-1}}{{f}_{p}}(z)$ is a Littlewood polynomial). We give explicit and recursive formulas for the limit of the ratio of  ${{L}^{q}}$ and
${{L}^{q}}$ and 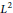 ${{L}^{2}}$ norm of
${{L}^{2}}$ norm of 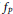 ${{f}_{p}}$ when
${{f}_{p}}$ when  $q$ is an even positive integer and
$q$ is an even positive integer and 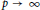 $p\to \infty $. To our knowledge, these are the first results that give these limiting values for specific sequences of nontrivial Littlewood polynomials and infinitely many
$p\to \infty $. To our knowledge, these are the first results that give these limiting values for specific sequences of nontrivial Littlewood polynomials and infinitely many  $q$. Similar results are given for polynomials obtained by cyclically permuting the coefficients of Fekete polynomials and for Littlewood polynomials whose coefficients are obtained from additive characters of finite fields. These results vastly generalise earlier results on the
$q$. Similar results are given for polynomials obtained by cyclically permuting the coefficients of Fekete polynomials and for Littlewood polynomials whose coefficients are obtained from additive characters of finite fields. These results vastly generalise earlier results on the 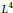 ${{L}^{4}}$ norm of these polynomials.
${{L}^{4}}$ norm of these polynomials.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017




