Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hovey, Mark
2001.
Model category structures on chain complexes of sheaves.
Transactions of the American Mathematical Society,
Vol. 353,
Issue. 6,
p.
2441.
Serpé, C.
2003.
Resolution of unbounded complexes in Grothendieck categories.
Journal of Pure and Applied Algebra,
Vol. 177,
Issue. 1,
p.
103.
Souto Salorio, María José
and
Trepode, Sonia
2003.
Ont-Structures and Tilting Theory.
Communications in Algebra,
Vol. 31,
Issue. 12,
p.
6093.
Tarrío, Leovigildo Alonso
López, Ana Jeremías
and
Salorio, María José
2003.
Construction of 𝑡-structures and equivalences of derived categories.
Transactions of the American Mathematical Society,
Vol. 355,
Issue. 6,
p.
2523.
GARKUSHA, GRIGORY
and
PREST, MIKE
2004.
INJECTIVE OBJECTS IN TRIANGULATED CATEGORIES.
Journal of Algebra and Its Applications,
Vol. 03,
Issue. 04,
p.
367.
Alonso Tarrı́o, Leovigildo
Jeremı́as López, Ana
and
Souto Salorio, Marı́a José
2004.
Bousfield localization on formal schemes.
Journal of Algebra,
Vol. 278,
Issue. 2,
p.
585.
Lowen, Wendy
and
Van den Bergh, Michel
2005.
Hochschild cohomology of abelian categories and ringed spaces.
Advances in Mathematics,
Vol. 198,
Issue. 1,
p.
172.
Van den Bergh, Michel
2007.
On global deformation quantization in the algebraic case.
Journal of Algebra,
Vol. 315,
Issue. 1,
p.
326.
Lieblich, Max
2007.
Moduli of twisted sheaves.
Duke Mathematical Journal,
Vol. 138,
Issue. 1,
Alonso Tarrío, Leovigildo
Jeremías López, Ana
Pérez Rodríguez, Marta
and
Vale Gonsalves, María J.
2008.
The derived category of quasi-coherent sheaves and axiomatic stable homotopy.
Advances in Mathematics,
Vol. 218,
Issue. 4,
p.
1224.
Grime, M.
2008.
Adjoint Functors and Triangulated Categories.
Communications in Algebra,
Vol. 36,
Issue. 10,
p.
3589.
Nicolás, Pedro
2008.
The bar derived category of a curved dg algebra.
Journal of Pure and Applied Algebra,
Vol. 212,
Issue. 12,
p.
2633.
Calaque, D.
Rossi, C. A.
and
van den Bergh, M.
2010.
Hochschild (Co)homology for Lie Algebroids.
International Mathematics Research Notices,
Varagnolo, Michela
and
Vasserot, Eric
2010.
Affine Flag Manifolds and Principal Bundles.
p.
233.
Krause, Henning
and
Šťovíček, Jan
2010.
The telescope conjecture for hereditary rings via Ext-orthogonal pairs.
Advances in Mathematics,
Vol. 225,
Issue. 5,
p.
2341.
Alonso Tarrío, Leovigildo
Jeremías López, Ana
and
Saorín, Manuel
2010.
Compactly generated t-structures on the derived category of a Noetherian ring.
Journal of Algebra,
Vol. 324,
Issue. 3,
p.
313.
Alonso Tarrío, Leovigildo
Jeremías López, Ana
Pérez Rodríguez, Marta
and
Vale Gonsalves, María J.
2011.
On the Existence of a Compact Generator on the Derived Category of a Noetherian Formal Scheme.
Applied Categorical Structures,
Vol. 19,
Issue. 6,
p.
865.
Neeman, Amnon
2011.
Colocalizing subcategories of D(R).
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2011,
Issue. 653,
Murfet, Daniel
2011.
Rouquier's Cocovering Theorem and Well-generated Triangulated Categories.
Journal of K-Theory,
Vol. 8,
Issue. 1,
p.
31.
Angeleri Hügel, Lidia
Koenig, Steffen
and
Liu, Qunhua
2011.
Recollements and tilting objects.
Journal of Pure and Applied Algebra,
Vol. 215,
Issue. 4,
p.
420.
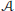 $\mathcal{A}$ and a complex
$\mathcal{A}$ and a complex 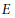 $E$ in
$E$ in 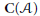 $\mathbf{C}(\mathcal{A})$ there is an associated localization endofunctor
$\mathbf{C}(\mathcal{A})$ there is an associated localization endofunctor 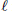 $\ell$ in
$\ell$ in 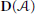 $\mathbf{D}(\mathcal{A})$. This means that
$\mathbf{D}(\mathcal{A})$. This means that 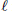 $\ell$ is idempotent (in a natural way) and that the objects that go to 0 by
$\ell$ is idempotent (in a natural way) and that the objects that go to 0 by 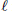 $\ell$ are those of the smallest localizing (= triangulated and stable for coproducts) subcategory of
$\ell$ are those of the smallest localizing (= triangulated and stable for coproducts) subcategory of 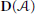 $\mathbf{D}(\mathcal{A})$ that contains
$\mathbf{D}(\mathcal{A})$ that contains 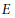 $E$. As applications, we construct
$E$. As applications, we construct 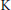 $\text{K}$-injective resolutions for complexes of objects of
$\text{K}$-injective resolutions for complexes of objects of 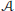 $\mathcal{A}$ and derive Brown representability for
$\mathcal{A}$ and derive Brown representability for 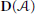 $\mathbf{D}(\mathcal{A})$ from the known result for
$\mathbf{D}(\mathcal{A})$ from the known result for 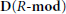 $\mathbf{D}(R-\mathbf{mod})$, where
$\mathbf{D}(R-\mathbf{mod})$, where 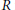 $R$ is a ring with unit.
$R$ is a ring with unit.

