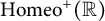1 Introduction
If
![]() $S$
is a nonempty set,
$S$
is a nonempty set,
![]() $\boldsymbol {{}^{\mathbb {R}} S}$
will denote the set of total functions from
$\boldsymbol {{}^{\mathbb {R}} S}$
will denote the set of total functions from
![]() $\mathbb {R}$
to
$\mathbb {R}$
to
![]() $S$
, and
$S$
, and
![]() $\boldsymbol {{}^{\underset {\smile }{\mathbb {R}}} S}$
will denote the set of all
$\boldsymbol {{}^{\underset {\smile }{\mathbb {R}}} S}$
will denote the set of all
![]() $S$
-valued functions
$S$
-valued functions
![]() $f$
such that
$f$
such that
![]() $\text {dom}(f)=(-\infty ,t_f)$
for some
$\text {dom}(f)=(-\infty ,t_f)$
for some
![]() $t_f \in \mathbb {R}$
. An
$t_f \in \mathbb {R}$
. An
![]() $\boldsymbol {S}$
-predictor will refer to any function
$\boldsymbol {S}$
-predictor will refer to any function
![]() $\mathcal {P}$
with domain and codomain as follows:
$\mathcal {P}$
with domain and codomain as follows:
If
![]() $f:(-\infty ,t_f) \to S$
is a member of
$f:(-\infty ,t_f) \to S$
is a member of
![]() ${}^{\underset {\smile }{\mathbb {R}}} S$
, we could view
${}^{\underset {\smile }{\mathbb {R}}} S$
, we could view
![]() $\mathcal {P}(f)$
as an attempt to predict which member of
$\mathcal {P}(f)$
as an attempt to predict which member of
![]() $S$
(which “state”) the function
$S$
(which “state”) the function
![]() $f$
would/should/will pick out at “time”
$f$
would/should/will pick out at “time”
![]() $t_f$
, if
$t_f$
, if
![]() $t_f$
were in its domain. We gauge how well
$t_f$
were in its domain. We gauge how well
![]() $\mathcal {P}$
makes predictions by asking: for which
$\mathcal {P}$
makes predictions by asking: for which
![]() $F \in {}^{\mathbb {R}} S$
and which
$F \in {}^{\mathbb {R}} S$
and which
![]() $t \in \mathbb {R}$
does
$t \in \mathbb {R}$
does
![]() $\mathcal {P}$
correctly predict
$\mathcal {P}$
correctly predict
![]() $F(t)$
, based solely on
$F(t)$
, based solely on
![]() $F|_{(-\infty ,t)}$
? That is, for which
$F|_{(-\infty ,t)}$
? That is, for which
![]() $F:\mathbb {R} \to S$
and
$F:\mathbb {R} \to S$
and
![]() $t \in \mathbb {R}$
does the equality
$t \in \mathbb {R}$
does the equality
hold?
If we restricted our attention to continuous
![]() $F:\mathbb {R} \to S$
(with respect to some nice topology on
$F:\mathbb {R} \to S$
(with respect to some nice topology on
![]() $S$
), then the problem would trivialize, since
$S$
), then the problem would trivialize, since
![]() $\mathcal {P}\Big ( F|_{(-\infty ,t)} \Big )$
could simply pick out
$\mathcal {P}\Big ( F|_{(-\infty ,t)} \Big )$
could simply pick out
![]() $\lim _{z \nearrow t} F(z)$
, which depends only on
$\lim _{z \nearrow t} F(z)$
, which depends only on
![]() $F|_{(-\infty , t)}$
. However, if
$F|_{(-\infty , t)}$
. However, if
![]() $|S|\ge 2$
, then it is impossible to find a
$|S|\ge 2$
, then it is impossible to find a
![]() $\mathcal {P}$
such that equation (*) holds for every function
$\mathcal {P}$
such that equation (*) holds for every function
![]() $F:\mathbb {R} \to S$
and every
$F:\mathbb {R} \to S$
and every
![]() $t \in \mathbb {R}$
. Simply fix any
$t \in \mathbb {R}$
. Simply fix any
![]() $f: (-\infty ,0) \to S$
; since
$f: (-\infty ,0) \to S$
; since
![]() $|S|\ge 2$
, there is a (possibly non-continuous) function
$|S|\ge 2$
, there is a (possibly non-continuous) function
![]() $F:\mathbb {R} \to S$
such that
$F:\mathbb {R} \to S$
such that
![]() $F|_{(-\infty ,0)}=f$
and
$F|_{(-\infty ,0)}=f$
and
![]() $F(0) \ne \mathcal {P}( f )$
. Then
$F(0) \ne \mathcal {P}( f )$
. Then
![]() $\mathcal {P} \Big ( F|_{(-\infty ,0)} \Big ) = \mathcal {P}(f) \ne F(0)$
, so
$\mathcal {P} \Big ( F|_{(-\infty ,0)} \Big ) = \mathcal {P}(f) \ne F(0)$
, so
![]() $\mathcal {P}$
failed to predict
$\mathcal {P}$
failed to predict
![]() $F(0)$
.
$F(0)$
.
Hardin and Taylor [Reference Hardin and Taylor5] considered what happens when we require the equality (*) to merely hold for almost every
![]() $t$
. We will say that an
$t$
. We will say that an
![]() $S$
-predictor
$S$
-predictor
![]() $\mathcal {P}$
is good if, for all total functions
$\mathcal {P}$
is good if, for all total functions
![]() $F: \mathbb {R} \to S$
, equation (*) holds for all except measure-zero many
$F: \mathbb {R} \to S$
, equation (*) holds for all except measure-zero many
![]() $t \in \mathbb {R}$
(where the measure zero set of “bad” predictions is allowed to depend on
$t \in \mathbb {R}$
(where the measure zero set of “bad” predictions is allowed to depend on
![]() $F$
). They proved the following.
$F$
). They proved the following.
Theorem 1 (Hardin and Taylor [Reference Hardin and Taylor5])
For every set
![]() $S$
, there exists a good
$S$
, there exists a good
![]() $S$
-predictor.
$S$
-predictor.
They showed in [Reference Hardin and Taylor6] that the
![]() $S$
-predictor could even be arranged to be independent of time shifts; i.e., to have the property that if
$S$
-predictor could even be arranged to be independent of time shifts; i.e., to have the property that if
![]() $f$
is some horizontal (constant) shift of
$f$
is some horizontal (constant) shift of
![]() $g$
, then
$g$
, then
![]() $\mathcal {P}(f)=\mathcal {P}(g)$
. They point out that this result has its roots in a 1965 problem of Galvin about “infinite hat” puzzles, which appeared in the problems section of the American Mathematical Monthly [Reference Galvin4]. The problem elicited an incorrect solution [Reference Silverman7] and a later correction [Reference Thorp8], both of which could be viewed as precursors to the key ideas in the various Hardin–Taylor results, and to the following question.
$\mathcal {P}(f)=\mathcal {P}(g)$
. They point out that this result has its roots in a 1965 problem of Galvin about “infinite hat” puzzles, which appeared in the problems section of the American Mathematical Monthly [Reference Galvin4]. The problem elicited an incorrect solution [Reference Silverman7] and a later correction [Reference Thorp8], both of which could be viewed as precursors to the key ideas in the various Hardin–Taylor results, and to the following question.
Question 2 (Paraphrase of Question 7.8.3 of [Reference Hardin and Taylor6])
How robust can a good predictor be, with respect to distortions in time?
More precisely, let
![]() $\mathrm{Homeo}^+(\mathbb {R})$
denote the group (under composition) of increasing homeomorphisms of
$\mathrm{Homeo}^+(\mathbb {R})$
denote the group (under composition) of increasing homeomorphisms of
![]() $\mathbb {R}$
. Following [Reference Hardin and Taylor6], if
$\mathbb {R}$
. Following [Reference Hardin and Taylor6], if
![]() $U \subseteq \mathrm{Homeo}^+(\mathbb {R})$
,Footnote
1
an
$U \subseteq \mathrm{Homeo}^+(\mathbb {R})$
,Footnote
1
an
![]() $S$
-predictor
$S$
-predictor
![]() $\mathcal {P}$
is called
$\mathcal {P}$
is called
![]() $\boldsymbol {U}$
-anonymous
Footnote
2
if
$\boldsymbol {U}$
-anonymous
Footnote
2
if
![]() $\mathcal {P}(f)=\mathcal {P}(f \circ \varphi )$
for all
$\mathcal {P}(f)=\mathcal {P}(f \circ \varphi )$
for all
![]() $\varphi \in U$
and all
$\varphi \in U$
and all
![]() $f \in {}^{\underset {\smile }{\mathbb {R}}} S$
. Since
$f \in {}^{\underset {\smile }{\mathbb {R}}} S$
. Since
![]() $\text {dom}(f) = (-\infty ,t_f)$
for some
$\text {dom}(f) = (-\infty ,t_f)$
for some
![]() $t_f \in \mathbb {R}$
, the domain of
$t_f \in \mathbb {R}$
, the domain of
![]() $f \circ \varphi $
is understood to be
$f \circ \varphi $
is understood to be
![]() $\Big (-\infty , \varphi ^{-1}(t_f)\Big )$
. See Figure 1 for an example (with
$\Big (-\infty , \varphi ^{-1}(t_f)\Big )$
. See Figure 1 for an example (with
![]() $S=\mathbb {R}$
).
$S=\mathbb {R}$
).

Figure 1:
![]() $f(x) = \sin (1/x)$
with domain
$f(x) = \sin (1/x)$
with domain
![]() $(-\infty ,0)$
, and
$(-\infty ,0)$
, and
![]() $\varphi (x)=x+e^{x+5}$
is a particular member of
$\varphi (x)=x+e^{x+5}$
is a particular member of
![]() $\mathrm{Homeo}^+(\mathbb {R})$
. If
$\mathrm{Homeo}^+(\mathbb {R})$
. If
![]() $\varphi \in U \subseteq \mathrm{Homeo}^+(\mathbb {R})$
and
$\varphi \in U \subseteq \mathrm{Homeo}^+(\mathbb {R})$
and
![]() $\mathcal {P}:{}^{\underset {\smile }{\mathbb {R}}} \mathbb {R} \to \mathbb {R}$
is a
$\mathcal {P}:{}^{\underset {\smile }{\mathbb {R}}} \mathbb {R} \to \mathbb {R}$
is a
![]() $U$
-anonymous
$U$
-anonymous
![]() $\mathbb {R}$
-predictor, then
$\mathbb {R}$
-predictor, then
![]() $\mathcal {P}(f)$
is required to be the same as
$\mathcal {P}(f)$
is required to be the same as
![]() $\mathcal {P}(f \circ \varphi )$
.
$\mathcal {P}(f \circ \varphi )$
.
So,
![]() $U$
-anonymity of
$U$
-anonymity of
![]() $\mathcal {P}$
means that
$\mathcal {P}$
means that
![]() $\mathcal {P}$
is insensitive to distortions in time caused by members of
$\mathcal {P}$
is insensitive to distortions in time caused by members of
![]() $U$
. The larger the set
$U$
. The larger the set
![]() $U$
, the more robust is the predictor
$U$
, the more robust is the predictor
![]() $\mathcal {P}$
. We already mentioned that Hardin and Taylor produced good predictors that were independent of horizontal shifts; using the terminology above, their theorem can be rephrased as: for every set
$\mathcal {P}$
. We already mentioned that Hardin and Taylor produced good predictors that were independent of horizontal shifts; using the terminology above, their theorem can be rephrased as: for every set
![]() $S$
, there is a good
$S$
, there is a good
![]() $S$
-predictor that is anonymous with respect to the group of shift functions (i.e., the group of functions of the form
$S$
-predictor that is anonymous with respect to the group of shift functions (i.e., the group of functions of the form
![]() $x \mapsto x + c$
for some constant
$x \mapsto x + c$
for some constant
![]() $c$
). This was improved by Bajpai and Velleman.
$c$
). This was improved by Bajpai and Velleman.
Theorem 3 (Bajpai and Velleman [Reference Bajpai and Velleman1])
For any set
![]() $S$
, there is a good
$S$
, there is a good
![]() $S$
-predictor that is anonymous with respect to
$S$
-predictor that is anonymous with respect to
![]() $\text {Aff}^{\kern2pt +}(\mathbb {R})$
(the group of affine functions of positive slope).
$\text {Aff}^{\kern2pt +}(\mathbb {R})$
(the group of affine functions of positive slope).
The Axiom of Choice was used in the proofs of both the Hardin–Taylor Theorem 1 and the Bajpai–Velleman Theorem 3, and in our improvement to be discussed below (Theorem 5). All of these results can be viewed as yet more strange consequences of the Axiom of Choice, the most famous of which are the Banach–Tarski Paradox and the existence of non-Lebesgue-measurable sets of reals. In [Reference Hardin and Taylor5], Hardin and Taylor state:
“We should emphasize that these results do not give a practical means of predicting the future, just as the time dilation one would experience standing near the event horizon of a black hole does not give a practical time machine. Nevertheless, we choose this presentation because we find it the most interesting, as well as pedagogically useful ….”
However, the Axiom of Choice is not a panacea for obtaining anonymous predictors. Even with the Axiom of Choice at their disposal, Bajpai and Velleman showed there is a limit to how robust predictors can be.
Theorem 4 (Bajpai and Velleman [Reference Bajpai and Velleman1])
There is an equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $\mathbb {R}$
such that, letting
$\mathbb {R}$
such that, letting
![]() $S:=\mathbb {R}/\sim $
, there is no good
$S:=\mathbb {R}/\sim $
, there is no good
![]() $S$
-predictor that is anonymous with respect to the set
$S$
-predictor that is anonymous with respect to the set
Clearly, if
![]() $U_0 \subset U_1$
, then a
$U_0 \subset U_1$
, then a
![]() $U_1$
-anonymous predictor is also
$U_1$
-anonymous predictor is also
![]() $U_0$
-anonymous. So, Theorems 3 and 4 provide “frontiers” in the subgroup lattice of
$U_0$
-anonymous. So, Theorems 3 and 4 provide “frontiers” in the subgroup lattice of
![]() $\mathrm{Homeo}^+(\mathbb {R})$
for how anonymous we can require predictors to be: the lower frontier is
$\mathrm{Homeo}^+(\mathbb {R})$
for how anonymous we can require predictors to be: the lower frontier is
![]() $\text {Aff}^{\kern2pt +}(\mathbb {R})$
, and the upper frontier is
$\text {Aff}^{\kern2pt +}(\mathbb {R})$
, and the upper frontier is
![]() $C^\infty (\mathbb {R}) \cap \mathrm{Homeo}^+(\mathbb {R})$
.
$C^\infty (\mathbb {R}) \cap \mathrm{Homeo}^+(\mathbb {R})$
.
Of course, this is a large gap, and [Reference Bajpai and Velleman1] closed by asking what happens between those two extremes. Our main results address this problem, thus chipping away at Question 2. Our new Theorems 5 and 8 are strengthenings of Theorems 3 and 4, respectively. In order to more flexibly derive examples, we state Theorem 5 in terms of
![]() $\mathrm{Homeo}^+(I)$
where
$\mathrm{Homeo}^+(I)$
where
![]() $I$
is any open interval of real numbers. See Section 3 for the meaning of good S-predictor in this context, which is the direct generalization of the definition given above (when
$I$
is any open interval of real numbers. See Section 3 for the meaning of good S-predictor in this context, which is the direct generalization of the definition given above (when
![]() $I=\mathbb {R}$
).
$I=\mathbb {R}$
).
Theorem 5 Suppose
![]() $I$
is an open interval of real numbers,
$I$
is an open interval of real numbers,
![]() $U$
is a subgroup of
$U$
is a subgroup of
![]() $\mathrm{Homeo}^+(I)$
, and:
$\mathrm{Homeo}^+(I)$
, and:
-
(1) the commutator subgroup of
 $U$
acts freely on
$U$
acts freely on
 $I$
;Footnote
3
and
$I$
;Footnote
3
and -
(2) each nonidentity member of
 $U$
has at most one fixed point.
$U$
has at most one fixed point.
Then, for any set
![]() $S$
, there is a good
$S$
, there is a good
![]() $U$
-anonymous
$U$
-anonymous
![]() $S$
-predictor.
$S$
-predictor.
The proof of Theorem 5 relies heavily on the ideas of the proofs in Bajpai–Velleman [Reference Bajpai and Velleman1] and Hardin–Taylor [Reference Hardin and Taylor5]. In fact, Theorem 5 is essentially the result of noticing that the Hardin–Taylor theorem about shift-anonymous predictors was essentially due to the classic group-theoretic Hölder’s Theorem discussed in Section 2, and that the Bajpai–Velleman strengthening was essentially about fixed points and commutator subgroups.
Corollary 6 We list several examples that satisfy the assumptions of Theorem 5.
-
(A) Bajpai–Velleman’s Theorem 3 is an immediate consequence of Theorem 5 (with
 $I=\mathbb {R}$
and
$I=\mathbb {R}$
and
 $U=\text {Aff}^{\kern2pt +}(\mathbb {R})$
), since the commutator subgroup of
$U=\text {Aff}^{\kern2pt +}(\mathbb {R})$
), since the commutator subgroup of
 $\text {Aff}^{\kern2pt +}(\mathbb {R})$
is exactly the group of shift functions (which act freely on
$\text {Aff}^{\kern2pt +}(\mathbb {R})$
is exactly the group of shift functions (which act freely on
 $\mathbb {R}$
), and nonidentity affine functions have at most one fixed point.
$\mathbb {R}$
), and nonidentity affine functions have at most one fixed point. -
(B) When
 $U \le \mathrm{Homeo}^+(I)$
and
$U \le \mathrm{Homeo}^+(I)$
and
 $U$
itself acts freely on
$U$
itself acts freely on
 $I$
, then
$I$
, then
 $U$
trivially satisfies both assumptions of Theorem 5. For example, this holds when
$U$
trivially satisfies both assumptions of Theorem 5. For example, this holds when
 $I=(0,1)$
and
$I=(0,1)$
and
 $U$
is the group of
$U$
is the group of
 $\varphi \in \mathrm{Homeo}^+(I)$
of the form
$\varphi \in \mathrm{Homeo}^+(I)$
of the form
 $x \mapsto x^\alpha $
for some
$x \mapsto x^\alpha $
for some
 $\alpha> 0$
(this
$\alpha> 0$
(this
 $U$
acts freely on
$U$
acts freely on
 $(0,1)$
).
$(0,1)$
). -
(C) If
 $U$
acts transitively on
$U$
acts transitively on
 $I$
,Footnote
4
the commutator subgroup of
$I$
,Footnote
4
the commutator subgroup of
 $U$
acts freely on
$U$
acts freely on
 $I$
, and each nonidentity member of
$I$
, and each nonidentity member of
 $U$
has only finitely many fixed points, then in fact each nonidentity member of
$U$
has only finitely many fixed points, then in fact each nonidentity member of
 $U$
has at most one fixed point (see Lemma 16 in Section 4 for a proof). Hence, Theorem 5 applies.
$U$
has at most one fixed point (see Lemma 16 in Section 4 for a proof). Hence, Theorem 5 applies. -
(D) (Special case of part (C)): suppose
 $U$
is a group of analytic functions in
$U$
is a group of analytic functions in
 $\mathrm{Homeo}^+\Big ( [0,1] \Big )$
; then it is well known that, since
$\mathrm{Homeo}^+\Big ( [0,1] \Big )$
; then it is well known that, since
 $[0,1]$
is compact, each nonidentity member of
$[0,1]$
is compact, each nonidentity member of
 $U$
has only finitely many fixed points.Footnote
5
Note that members of
$U$
has only finitely many fixed points.Footnote
5
Note that members of
 $U$
also act on the set
$U$
also act on the set
 $(0,1)$
. So, if
$(0,1)$
. So, if
 $U$
acts transitively on
$U$
acts transitively on
 $(0,1)$
and the commutator subgroup of
$(0,1)$
and the commutator subgroup of
 $U$
acts freely on
$U$
acts freely on
 $(0,1)$
, then we are in the setting of part (C), with
$(0,1)$
, then we are in the setting of part (C), with
 $I=(0,1)$
(and where we replace
$I=(0,1)$
(and where we replace
 $U$
by
$U$
by
 $\{ \varphi \restriction (0,1) \ : \ \varphi \in U \}$
).
$\{ \varphi \restriction (0,1) \ : \ \varphi \in U \}$
). -
(E) If
 $\varphi \in \mathrm{Homeo}^+(I)$
and
$\varphi \in \mathrm{Homeo}^+(I)$
and
 $\varphi $
has only measure zero many fixed points, then for every set
$\varphi $
has only measure zero many fixed points, then for every set
 $S$
, there exists a
$S$
, there exists a
 $\langle \varphi \rangle $
-invariant, good
$\langle \varphi \rangle $
-invariant, good
 $S$
-predictor (where
$S$
-predictor (where
 $\langle \varphi \rangle $
denotes the cyclic group generated by
$\langle \varphi \rangle $
denotes the cyclic group generated by
 $\varphi $
). See Section 4 for why this follows from Theorem 5. In particular, this holds whenever
$\varphi $
). See Section 4 for why this follows from Theorem 5. In particular, this holds whenever
 $\varphi $
has only countably many fixed points (e.g., for any nonidentity analytic function in
$\varphi $
has only countably many fixed points (e.g., for any nonidentity analytic function in
 $\mathrm{Homeo}^+(I)$
).
$\mathrm{Homeo}^+(I)$
).
Remark 7 Since the assumptions of Theorem 5 are phrased entirely in terms of continuous group actions, examples of
![]() $U$
with those properties transfer via homeomorphisms. For example, if
$U$
with those properties transfer via homeomorphisms. For example, if
![]() $I=(0,1)$
and
$I=(0,1)$
and
are as in part (B) of the corollary, and
![]() $\Psi : (0,1) \to \mathbb {R}$
is a homeomorphism, then
$\Psi : (0,1) \to \mathbb {R}$
is a homeomorphism, then
is a subgroup of
![]() $\mathrm{Homeo}^+(\mathbb {R})$
that satisfies the assumptions of Theorem 5.
$\mathrm{Homeo}^+(\mathbb {R})$
that satisfies the assumptions of Theorem 5.
We also strengthen the “upper frontier” from Bajpai–Velleman’s Theorem 4.
Theorem 8 There is an equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $\mathbb {R}$
such that, letting
$\mathbb {R}$
such that, letting
![]() $S:=\mathbb {R}/\sim $
, there is no good
$S:=\mathbb {R}/\sim $
, there is no good
![]() $S$
-predictor that is anonymous with respect to the group of infinitely Lipschitz diffeomorphisms. (In fact, we show there is no good “weak”
$S$
-predictor that is anonymous with respect to the group of infinitely Lipschitz diffeomorphisms. (In fact, we show there is no good “weak”
![]() $S$
-predictor that is anonymous with respect to this class; see Section 5 for the relevant definitions.)
$S$
-predictor that is anonymous with respect to this class; see Section 5 for the relevant definitions.)
Section 2 provides the relevant background about Hölder’s Theorem, Section 3 proves Theorem 5, Section 4 proves Corollary 6, and Section 5 proves Theorem 8. The only prerequisites are very basic group theory and real analysis; in particular, no set-theoretic background whatsoever is assumed of the reader. The only set-theoretic ingredient is the use of a wellorder in the proof of Theorem 5 in Section 3. A wellorder is a linear order with no infinite descending chain. The Axiom of Choice ensures that every set can be wellordered, which we will use exactly once (on page 7) to obtain a wellorder of the set
By wellordered set of reals, we will mean a set
![]() $X \subset \mathbb {R}$
such that
$X \subset \mathbb {R}$
such that
![]() $(X,<)$
is a wellorder, where
$(X,<)$
is a wellorder, where
![]() $<$
denotes the usual ordering of
$<$
denotes the usual ordering of
![]() $\mathbb {R}$
. The following fact is key (see [Reference Hardin and Taylor5, Corollary 3.4]).
$\mathbb {R}$
. The following fact is key (see [Reference Hardin and Taylor5, Corollary 3.4]).
Fact 9 Every wellordered set of reals is countable (hence, has Lebesgue measure zero).
2 Hölder’s Theorem and its consequences
An Archimedean ordered group is a triple
![]() $(G,\cdot , <)$
such that
$(G,\cdot , <)$
such that
![]() $(G,\cdot )$
is a group,
$(G,\cdot )$
is a group,
![]() $<$
is a linear order on
$<$
is a linear order on
![]() $G$
, and:
$G$
, and:
-
(1)
 $<$
is both left and right invariant with respect to the group operation, meaning that for all
$<$
is both left and right invariant with respect to the group operation, meaning that for all
 $a,b,c \in G$
:Footnote
6
$a,b,c \in G$
:Footnote
6
 $$\begin{align*}a < b \implies ca < cb \ \text{ and } \ ac < bc; \end{align*}$$
$$\begin{align*}a < b \implies ca < cb \ \text{ and } \ ac < bc; \end{align*}$$
-
(2) whenever
 $1 < a < b$
, there is an
$1 < a < b$
, there is an
 $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
 $b < a^n$
.
$b < a^n$
.
We also say that an (un-ordered) group
![]() $(G,\cdot )$
is Archimedean if there exists a linear order
$(G,\cdot )$
is Archimedean if there exists a linear order
![]() $<$
on
$<$
on
![]() $G$
such that
$G$
such that
![]() $(G,\cdot ,<)$
is an Archimedean ordered group.
$(G,\cdot ,<)$
is an Archimedean ordered group.
Theorem 10 (Hölder’s Theorem; see Chapter IV, Theorem 1 of [Reference Fuchs3])
Every Archimedean group is abelian.Footnote 7
Hölder’s Theorem is relevant for the study of continuous group actions on the reals.
Theorem 11 (Folklore; special case of Theorem 4 of [Reference Farb and Shalen2])
Suppose
![]() $I$
is an open interval of real numbers and
$I$
is an open interval of real numbers and
![]() $V$
is a subgroup of
$V$
is a subgroup of
![]() $\mathrm{Homeo}^+(I)$
that acts freely on
$\mathrm{Homeo}^+(I)$
that acts freely on
![]() $I$
. Then the binary relation
$I$
. Then the binary relation
![]() $\prec $
on
$\prec $
on
![]() $V$
defined by
$V$
defined by
is an Archimedean order on
![]() $V$
. Consequently, by Hölder’s Theorem,
$V$
. Consequently, by Hölder’s Theorem,
![]() $V$
is abelian.
$V$
is abelian.
Since Theorem 11 is so central to the paper (in the key Lemma 13), we give a sketch of the proof. Fix any
![]() $x_0 \in I$
, and define the relation
$x_0 \in I$
, and define the relation
![]() $\prec _{x_0}$
on
$\prec _{x_0}$
on
![]() $V$
by:
$V$
by:
![]() $\varphi \prec _{x_0} \psi $
if
$\varphi \prec _{x_0} \psi $
if
![]() $\varphi (x_0) < \psi (x_0)$
. The relation
$\varphi (x_0) < \psi (x_0)$
. The relation
![]() $\prec _{x_0}$
is clearly transitive and antisymmetric. It is total, because if
$\prec _{x_0}$
is clearly transitive and antisymmetric. It is total, because if
![]() $\varphi ,\psi \in V$
and
$\varphi ,\psi \in V$
and
![]() $\varphi (x_0) = \psi (x_0)$
, then
$\varphi (x_0) = \psi (x_0)$
, then
![]() $\psi ^{-1} \circ \varphi $
fixes
$\psi ^{-1} \circ \varphi $
fixes
![]() $x_0$
, and hence (since
$x_0$
, and hence (since
![]() $V$
acts freely on
$V$
acts freely on
![]() $I$
)
$I$
)
![]() $\psi ^{-1} \circ \varphi = \text {id}$
; i.e.,
$\psi ^{-1} \circ \varphi = \text {id}$
; i.e.,
![]() $\varphi =\psi $
. So
$\varphi =\psi $
. So
![]() $\prec _{x_0}$
is a linear order on
$\prec _{x_0}$
is a linear order on
![]() $V$
. The Intermediate Value Theorem, together with the assumption that
$V$
. The Intermediate Value Theorem, together with the assumption that
![]() $V$
acts freely on
$V$
acts freely on
![]() $I$
, ensure that
$I$
, ensure that
![]() $\prec _{x_0}$
is the same as the relation
$\prec _{x_0}$
is the same as the relation
![]() $\prec $
defined in the statement of Theorem 11. This relation is also left and right invariant with respect to composition (on
$\prec $
defined in the statement of Theorem 11. This relation is also left and right invariant with respect to composition (on
![]() $V$
). Finally, to see that
$V$
). Finally, to see that
![]() $\prec _{x_0}$
is Archimedean, suppose
$\prec _{x_0}$
is Archimedean, suppose
![]() $\text {id} \prec _{x_0} \varphi \prec _{x_0} \psi $
with
$\text {id} \prec _{x_0} \varphi \prec _{x_0} \psi $
with
![]() $\varphi ,\psi \in V$
. Then
$\varphi ,\psi \in V$
. Then
![]() $\text {id} \prec \varphi $
, and hence
$\text {id} \prec \varphi $
, and hence
![]() $\langle \varphi ^n(x_0) \ : \ n \in \mathbb {N} \rangle $
is a strictly increasing sequence. So it either converges to a point in
$\langle \varphi ^n(x_0) \ : \ n \in \mathbb {N} \rangle $
is a strictly increasing sequence. So it either converges to a point in
![]() $I$
, or to “
$I$
, or to “
![]() $+\infty $
” (the right endpoint of
$+\infty $
” (the right endpoint of
![]() $I$
). It cannot converge to a point in
$I$
). It cannot converge to a point in
![]() $I$
, because if it did, that limit would be a fixed point of the continuous (nonidentity) function
$I$
, because if it did, that limit would be a fixed point of the continuous (nonidentity) function
![]() $\varphi $
, contradicting that
$\varphi $
, contradicting that
![]() $\varphi \in V$
and
$\varphi \in V$
and
![]() $V$
acts freely. So
$V$
acts freely. So
![]() $\lim _{n \to \infty } \varphi ^n(x_0) = \infty $
; hence, there is some
$\lim _{n \to \infty } \varphi ^n(x_0) = \infty $
; hence, there is some
![]() $n$
such that
$n$
such that
![]() $\psi (x_0) < \varphi ^n(x_0)$
. Then
$\psi (x_0) < \varphi ^n(x_0)$
. Then
![]() $\psi \prec _{x_0} \varphi ^n$
, which is equivalent to saying
$\psi \prec _{x_0} \varphi ^n$
, which is equivalent to saying
![]() $\psi \prec \varphi ^n$
.
$\psi \prec \varphi ^n$
.
3 Proof of Theorem 5
In this section, we prove Theorem 5. If
![]() $I$
is an open interval of real numbers, the lower and upper endpoints of
$I$
is an open interval of real numbers, the lower and upper endpoints of
![]() $I$
will be denoted
$I$
will be denoted
![]() $-\infty $
and
$-\infty $
and
![]() $\infty $
, respectively. If
$\infty $
, respectively. If
![]() $S$
is a nonempty set,
$S$
is a nonempty set,
![]() $\boldsymbol {{}^I S}$
denotes the set of total functions from
$\boldsymbol {{}^I S}$
denotes the set of total functions from
![]() $I$
to
$I$
to
![]() $S$
, and
$S$
, and
![]() $\boldsymbol {{}^{\underset {\smile }{I}} S}$
denotes the set of functions of the form
$\boldsymbol {{}^{\underset {\smile }{I}} S}$
denotes the set of functions of the form
![]() $f: (-\infty ,t_f) \to S$
for some
$f: (-\infty ,t_f) \to S$
for some
![]() $t_f \in I$
. Uppercase and lowercase letters will be used for members of
$t_f \in I$
. Uppercase and lowercase letters will be used for members of
![]() ${}^I S$
and
${}^I S$
and
![]() ${}^{\underset {\smile }{I}} S$
, respectively, but note that if
${}^{\underset {\smile }{I}} S$
, respectively, but note that if
![]() $F \in {}^I S$
and
$F \in {}^I S$
and
![]() $t \in I$
, then
$t \in I$
, then
![]() $F|_{(-\infty ,t)}$
is a member of
$F|_{(-\infty ,t)}$
is a member of
![]() ${}^{\underset {\smile }{I}} S$
.
${}^{\underset {\smile }{I}} S$
.
The notions of good and anonymous
![]() $S$
-predictors in this context are the obvious generalizations of the definitions given in the introduction (which were for the special case
$S$
-predictors in this context are the obvious generalizations of the definitions given in the introduction (which were for the special case
![]() $I=\mathbb {R}$
); i.e., a good
$I=\mathbb {R}$
); i.e., a good
![]() $S$
-predictor is a function
$S$
-predictor is a function
![]() $\mathcal {P}: {}^{\underset {\smile }{I}} S \to S$
such that for all
$\mathcal {P}: {}^{\underset {\smile }{I}} S \to S$
such that for all
![]() $F \in {}^I S$
,
$F \in {}^I S$
,
If
![]() $U \subseteq \mathrm{Homeo}^+(I)$
, we say that a function
$U \subseteq \mathrm{Homeo}^+(I)$
, we say that a function
![]() $\mathcal {P}$
with domain
$\mathcal {P}$
with domain
![]() ${}^{\underset {\smile }{I}} S$
is
${}^{\underset {\smile }{I}} S$
is
![]() $U$
-anonymous if
$U$
-anonymous if
![]() $\mathcal {P}(f) = \mathcal {P}(f \circ \varphi )$
for every
$\mathcal {P}(f) = \mathcal {P}(f \circ \varphi )$
for every
![]() $f \in {}^{\underset {\smile }{I}} S$
and every
$f \in {}^{\underset {\smile }{I}} S$
and every
![]() $\varphi \in U$
.
$\varphi \in U$
.
Lowercase Greek letters are reserved for elements of
![]() $\mathrm{Homeo}^+(I)$
. If
$\mathrm{Homeo}^+(I)$
. If
![]() $\varphi \in \mathrm{Homeo}^+(I)$
and
$\varphi \in \mathrm{Homeo}^+(I)$
and
![]() $n \in \mathbb {Z}$
,
$n \in \mathbb {Z}$
,
![]() $\varphi ^n$
denotes the
$\varphi ^n$
denotes the
![]() $n$
-fold composition of
$n$
-fold composition of
![]() $\varphi $
if
$\varphi $
if
![]() $n \ge 1$
,
$n \ge 1$
,
![]() $\text {id}_I$
if
$\text {id}_I$
if
![]() $n=0$
, and the
$n=0$
, and the
![]() $|n|$
-fold composition of
$|n|$
-fold composition of
![]() $\varphi ^{-1}$
if
$\varphi ^{-1}$
if
![]() $n < 0$
.
$n < 0$
.
If
![]() $F:I \to S$
and
$F:I \to S$
and
![]() $\varphi \in \mathrm{Homeo}(I)$
, we say that
$\varphi \in \mathrm{Homeo}(I)$
, we say that
![]() $\boldsymbol {F}$
is
$\boldsymbol {F}$
is
![]() $\boldsymbol {\varphi }$
-invariant if
$\boldsymbol {\varphi }$
-invariant if
![]() $F = F \circ \varphi $
, and
$F = F \circ \varphi $
, and
![]() $\boldsymbol {F}$
is
$\boldsymbol {F}$
is
![]() $\boldsymbol {\varphi }$
-invariant before
$\boldsymbol {\varphi }$
-invariant before
![]() $\boldsymbol {t}$
if
$\boldsymbol {t}$
if
We say that
![]() $\boldsymbol {F}$
is past
$\boldsymbol {F}$
is past
![]() $\boldsymbol {\varphi }$
-invariant if there is some
$\boldsymbol {\varphi }$
-invariant if there is some
![]() $t \in I$
such that
$t \in I$
such that
![]() $F$
is
$F$
is
![]() $\varphi $
-invariant before
$\varphi $
-invariant before
![]() $t$
.
$t$
.
Lemma 12 (Analogue of Lemmas 2 and 3 of [Reference Bajpai and Velleman1])
Suppose
![]() $F \in {}^I S$
,
$F \in {}^I S$
,
![]() $\varphi \in \mathrm{Homeo}^+(I)$
, and
$\varphi \in \mathrm{Homeo}^+(I)$
, and
![]() $F$
is
$F$
is
![]() $\varphi $
-invariant before
$\varphi $
-invariant before
![]() $t$
. Then there is an
$t$
. Then there is an
![]() $H:I \to S$
that extends
$H:I \to S$
that extends
![]() $F|_{(-\infty ,t)}$
and is
$F|_{(-\infty ,t)}$
and is
![]() $\varphi $
-invariant.
$\varphi $
-invariant.
Proof Since
![]() $\varphi $
is invertible, the relation
$\varphi $
is invertible, the relation
is an equivalence relation on
![]() $I$
. Suppose
$I$
. Suppose
![]() $x \sim z$
; without loss of generality, say
$x \sim z$
; without loss of generality, say
![]() $n \ge 0$
and
$n \ge 0$
and
![]() $\varphi ^n(x) = z$
. Then, because
$\varphi ^n(x) = z$
. Then, because
![]() $\varphi $
is order-preserving, the sequence
$\varphi $
is order-preserving, the sequence
![]() $\Big ( \varphi ^k(x) \Big )_{k \ge 0}$
is monotonic (increasing if
$\Big ( \varphi ^k(x) \Big )_{k \ge 0}$
is monotonic (increasing if
![]() $x \le \varphi (x)$
, and decreasing if
$x \le \varphi (x)$
, and decreasing if
![]() $x \ge \varphi (x)$
). In particular, if both
$x \ge \varphi (x)$
). In particular, if both
![]() $x$
and
$x$
and
![]() $z$
are less than
$z$
are less than
![]() $t$
, then so is
$t$
, then so is
![]() $\varphi ^k(x)$
for every integer
$\varphi ^k(x)$
for every integer
![]() $k$
between
$k$
between
![]() $0$
and
$0$
and
![]() $n$
. Since
$n$
. Since
![]() $F$
is
$F$
is
![]() $\varphi $
-invariant before
$\varphi $
-invariant before
![]() $t$
, it follows that
$t$
, it follows that
![]() $F(x) = F(\varphi ^k(x))$
for each
$F(x) = F(\varphi ^k(x))$
for each
![]() $k$
between
$k$
between
![]() $0$
and
$0$
and
![]() $n$
; in particular,
$n$
; in particular,
![]() $F(x)=F(z)$
.
$F(x)=F(z)$
.
Hence, for any equivalence class
![]() $C$
, if
$C$
, if
![]() $C \cap (-\infty ,t) \ne \emptyset $
, then the restriction of
$C \cap (-\infty ,t) \ne \emptyset $
, then the restriction of
![]() $F$
to
$F$
to
![]() $C \cap (-\infty ,t)$
is constant; let
$C \cap (-\infty ,t)$
is constant; let
![]() $s_C$
denote this constant value. Now, fix any
$s_C$
denote this constant value. Now, fix any
![]() $s^* \in S$
, and define
$s^* \in S$
, and define
![]() $H:I \to S$
by
$H:I \to S$
by
 $$\begin{align*}H(y)= \begin{cases} s_{[y]}, & \text{ if } [y] \cap (-\infty,t) \ne \emptyset, \\ s^*, & \text{ otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}H(y)= \begin{cases} s_{[y]}, & \text{ if } [y] \cap (-\infty,t) \ne \emptyset, \\ s^*, & \text{ otherwise,} \end{cases} \end{align*}$$
where
![]() $[y]$
denotes the equivalence class of
$[y]$
denotes the equivalence class of
![]() $y$
. Then
$y$
. Then
![]() $H$
extends
$H$
extends
![]() $F|_{(-\infty ,t)}$
, and, since
$F|_{(-\infty ,t)}$
, and, since
![]() $[y]=[\varphi (y)]$
for every
$[y]=[\varphi (y)]$
for every
![]() $y \in I$
,
$y \in I$
,
![]() $H$
is
$H$
is
![]() $\varphi $
-invariant.
$\varphi $
-invariant.
The next lemma is the key use of free actions and Hölder’s Theorem.
Lemma 13 (Analogue of Lemma 4 of [Reference Bajpai and Velleman1])
Suppose
![]() $V$
is a subgroup of
$V$
is a subgroup of
![]() $\mathrm{Homeo}^+(I)$
and
$\mathrm{Homeo}^+(I)$
and
![]() $V$
acts freely on
$V$
acts freely on
![]() $I$
. Suppose
$I$
. Suppose
![]() $F: \mathbb {R} \to S$
is invariant with respect to some nonidentity member of
$F: \mathbb {R} \to S$
is invariant with respect to some nonidentity member of
![]() $V$
. Then, for any
$V$
. Then, for any
![]() $\varphi \in V$
: if
$\varphi \in V$
: if
![]() $F$
is past
$F$
is past
![]() $\varphi $
-invariant, then
$\varphi $
-invariant, then
![]() $F$
is (fully)
$F$
is (fully)
![]() $\varphi $
-invariant.
$\varphi $
-invariant.
Proof By assumption, there is a
![]() $\psi \in V$
such that
$\psi \in V$
such that
![]() $\psi \ne \text {id}$
and
$\psi \ne \text {id}$
and
![]() $F$
is
$F$
is
![]() $\psi $
-invariant. Now, suppose
$\psi $
-invariant. Now, suppose
![]() $\varphi \in V$
and
$\varphi \in V$
and
![]() $F$
is past
$F$
is past
![]() $\varphi $
-invariant; recall this means there is some
$\varphi $
-invariant; recall this means there is some
![]() $t \in I$
such that
$t \in I$
such that
![]() $F$
is
$F$
is
![]() $\varphi $
-invariant before
$\varphi $
-invariant before
![]() $t$
(i.e., if
$t$
(i.e., if
![]() $z < t$
, then
$z < t$
, then
![]() $F(\varphi (z)) = F(z)$
). Fix any
$F(\varphi (z)) = F(z)$
). Fix any
![]() $x \in I$
; we want to show
$x \in I$
; we want to show
![]() $F(\varphi (x)) = F(x)$
. Since
$F(\varphi (x)) = F(x)$
. Since
![]() $\psi \ne \text {id}$
and
$\psi \ne \text {id}$
and
![]() $V$
acts freely,
$V$
acts freely,
![]() $\psi $
has no fixed points. Let
$\psi $
has no fixed points. Let
![]() $\prec $
be the linear order on
$\prec $
be the linear order on
![]() $V$
given by Theorem 11. Then either
$V$
given by Theorem 11. Then either
![]() $\psi \prec \text {id}$
or
$\psi \prec \text {id}$
or
![]() $\psi ^{-1} \prec \text {id}$
. Without loss of generality,Footnote
8
we can assume that
$\psi ^{-1} \prec \text {id}$
. Without loss of generality,Footnote
8
we can assume that
![]() $\psi \prec \text {id}$
. Then
$\psi \prec \text {id}$
. Then
![]() $\langle \psi ^n(x) \ : \ n \in \mathbb {N} \rangle $
is a strictly decreasing sequence. Since
$\langle \psi ^n(x) \ : \ n \in \mathbb {N} \rangle $
is a strictly decreasing sequence. Since
![]() $\psi $
is continuous and has no fixed points, it follows that
$\psi $
is continuous and has no fixed points, it follows that
![]() $\lim _{n \to \infty } \psi ^n(x) = -\infty $
. So, for some
$\lim _{n \to \infty } \psi ^n(x) = -\infty $
. So, for some
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\psi ^n(x) < t$
. Then
$\psi ^n(x) < t$
. Then
 $$ \begin{align*} F(x) & = F\big( \psi^n(x) \big) & \text{ (because }F \text{ is }\psi\text{-invariant)} \\& = F\big( \varphi(\psi^n(x)) \big) & \text{ (because }\psi^n(x) < t \text{ and } F \text{ is } \varphi\text{-invariant before }t)\\& = F\big( \psi^n(\varphi(x)) \big) & \text{ (because } V \text{ is abelian, by Theorem }11) \\& = F(\varphi(x)) & \text{ (because }F \text{ is }\psi\text{-invariant).} \end{align*} $$
$$ \begin{align*} F(x) & = F\big( \psi^n(x) \big) & \text{ (because }F \text{ is }\psi\text{-invariant)} \\& = F\big( \varphi(\psi^n(x)) \big) & \text{ (because }\psi^n(x) < t \text{ and } F \text{ is } \varphi\text{-invariant before }t)\\& = F\big( \psi^n(\varphi(x)) \big) & \text{ (because } V \text{ is abelian, by Theorem }11) \\& = F(\varphi(x)) & \text{ (because }F \text{ is }\psi\text{-invariant).} \end{align*} $$
A commutator in a group is an element of the form
![]() $aba^{-1} b^{-1}$
. If
$aba^{-1} b^{-1}$
. If
![]() $U$
is a group,
$U$
is a group,
![]() $\boldsymbol {[U,U]}$
denotes the commutator subgroup of U, which is the subgroup generated by the commutators. At one point, we will use the basic group-theoretic fact that
$\boldsymbol {[U,U]}$
denotes the commutator subgroup of U, which is the subgroup generated by the commutators. At one point, we will use the basic group-theoretic fact that
We now commence with the proof of Theorem 5. Fix any nonempty set
![]() $S$
for the remainder of this section. Assume that
$S$
for the remainder of this section. Assume that
![]() $I$
is an open interval of real numbers and
$I$
is an open interval of real numbers and
![]() $U$
is a subgroup of
$U$
is a subgroup of
![]() $\mathrm{Homeo}^+(I)$
such that:
$\mathrm{Homeo}^+(I)$
such that:
-
(1)
 $[U,U]$
acts freely on
$[U,U]$
acts freely on
 $I$
, and
$I$
, and -
(2) each nonidentity member of
 $U$
has at most one fixed point.
$U$
has at most one fixed point.
Define the following subsets of
![]() ${}^I S$
:
${}^I S$
:
-
•
 $\text {Inv}_{[U,U]}:=$
the set of functions in
$\text {Inv}_{[U,U]}:=$
the set of functions in
 ${}^I S$
that are invariant with respect to some nonidentity member of
${}^I S$
that are invariant with respect to some nonidentity member of
 $[U,U]$
.
$[U,U]$
. -
•
 $\text {Inv}_{U}:=$
the set of functions in
$\text {Inv}_{U}:=$
the set of functions in
 ${}^I S$
that are invariant with respect to some nonidentity member of
${}^I S$
that are invariant with respect to some nonidentity member of
 $U$
.
$U$
.
By the Axiom of Choice, there exists a wellordering
![]() $\triangleleft $
of
$\triangleleft $
of
![]() ${}^I S$
such that
${}^I S$
such that
![]() $\text {Inv}_{[U,U]}$
functions are listed first, then functions in
$\text {Inv}_{[U,U]}$
functions are listed first, then functions in
![]() $\text {Inv}_U \setminus \text {Inv}_{[U,U]}$
, then the rest of
$\text {Inv}_U \setminus \text {Inv}_{[U,U]}$
, then the rest of
![]() ${}^I S$
.Footnote
9
The reason for these requirements will become apparent in the proof of Claim 14.
${}^I S$
.Footnote
9
The reason for these requirements will become apparent in the proof of Claim 14.
Recall from the discussion of anonymity in Section 1 that if
![]() $f \in {}^{\underset {\smile }{I}} S$
and
$f \in {}^{\underset {\smile }{I}} S$
and
![]() $\varphi \in \mathrm{Homeo}^+(I)$
,
$\varphi \in \mathrm{Homeo}^+(I)$
,
![]() $f \circ \varphi $
is understood to have domain
$f \circ \varphi $
is understood to have domain
![]() $\big (-\infty , \varphi ^{-1}(t_f) \big )$
. Define
$\big (-\infty , \varphi ^{-1}(t_f) \big )$
. Define
![]() $\boldsymbol { f \circ U}$
to be the set of functions of the form
$\boldsymbol { f \circ U}$
to be the set of functions of the form
![]() $f \circ \varphi $
, where
$f \circ \varphi $
, where
![]() $\varphi \in U$
. Let
$\varphi \in U$
. Let
![]() $\boldsymbol {\overline {f \circ U}}$
denote the collection of all (total)
$\boldsymbol {\overline {f \circ U}}$
denote the collection of all (total)
![]() $F: I \to S$
such that
$F: I \to S$
such that
![]() $F$
extends at least one member of
$F$
extends at least one member of
![]() $f \circ U$
. Note that a given
$f \circ U$
. Note that a given
![]() $F \in \overline {f \circ U}$
may possibly extend more than one member of
$F \in \overline {f \circ U}$
may possibly extend more than one member of
![]() $f \circ U$
;Footnote
10
in fact, dealing with this issue is the heart of the argument. Let
$f \circ U$
;Footnote
10
in fact, dealing with this issue is the heart of the argument. Let
![]() $F_{f \circ U}$
denote the
$F_{f \circ U}$
denote the
![]() $\triangleleft $
-least member of the set
$\triangleleft $
-least member of the set
![]() $\overline {f \circ U}$
.
$\overline {f \circ U}$
.
Part (2) of the following claim is the key use of Lemma 13, which was a consequence of Hölder’s Theorem.
Claim 14 Suppose
![]() $f:(-\infty ,t_f) \to S$
,
$f:(-\infty ,t_f) \to S$
,
![]() $\varphi \in U$
, and
$\varphi \in U$
, and
![]() $F_{f \circ U}$
extends
$F_{f \circ U}$
extends
![]() $f \circ \varphi $
. Suppose
$f \circ \varphi $
. Suppose
![]() $\gamma \in U$
,
$\gamma \in U$
,
![]() $\gamma \ne \text {id}_I$
, and
$\gamma \ne \text {id}_I$
, and
![]() $F_{f \circ U}$
is
$F_{f \circ U}$
is
![]() $\gamma $
-invariant before
$\gamma $
-invariant before
![]() $\varphi ^{-1}(t_f)$
(i.e., for inputs that come from the domain of
$\varphi ^{-1}(t_f)$
(i.e., for inputs that come from the domain of
![]() $f \circ \varphi $
). Then:
$f \circ \varphi $
). Then:
-
(1)
 $F_{f \circ U} \in \text {Inv}_{U}$
(i.e.,
$F_{f \circ U} \in \text {Inv}_{U}$
(i.e.,
 $F_{f \circ U}$
is fully invariant with respect to some nonidentity member of
$F_{f \circ U}$
is fully invariant with respect to some nonidentity member of
 $U$
, though not necessarily with respect to
$U$
, though not necessarily with respect to
 $\gamma $
).
$\gamma $
). -
(2) If
 $\gamma \in [U,U]$
, then
$\gamma \in [U,U]$
, then
 $F_{f \circ U}$
is fully
$F_{f \circ U}$
is fully
 $\gamma $
-invariant.
$\gamma $
-invariant.
Proof By Lemma 12, there is an
![]() $H:\mathbb {R} \to S$
that extends
$H:\mathbb {R} \to S$
that extends
![]() $F_{f \circ U}|_{\big (-\infty , \varphi ^{-1}(t_f) \big )}$
(
$F_{f \circ U}|_{\big (-\infty , \varphi ^{-1}(t_f) \big )}$
(
![]() $=f \circ \varphi $
) and is
$=f \circ \varphi $
) and is
![]() $\gamma $
-invariant. Then
$\gamma $
-invariant. Then
![]() $H \in \overline {f \circ U} \cap \text {Inv}_U$
. Since
$H \in \overline {f \circ U} \cap \text {Inv}_U$
. Since
![]() $F_{f \circ U}$
is the
$F_{f \circ U}$
is the
![]() $\triangleleft $
-least member of
$\triangleleft $
-least member of
![]() $\overline {f \circ U}$
,
$\overline {f \circ U}$
,
![]() $F_{f \circ U} \trianglelefteq H$
. And since
$F_{f \circ U} \trianglelefteq H$
. And since
![]() $H \in \text {Inv}_U$
and
$H \in \text {Inv}_U$
and
![]() $\triangleleft $
lists members of
$\triangleleft $
lists members of
![]() $\text {Inv}_U$
before members of
$\text {Inv}_U$
before members of
![]() ${}^I S \setminus \text {Inv}_U$
, it follows that
${}^I S \setminus \text {Inv}_U$
, it follows that
![]() $F_{f \circ U} \in \text {Inv}_U$
. This proves part (1).
$F_{f \circ U} \in \text {Inv}_U$
. This proves part (1).
If
![]() $\gamma $
was an element of
$\gamma $
was an element of
![]() $[U,U]$
, then
$[U,U]$
, then
![]() $H \in \overline {f \circ U} \cap \text {Inv}_{[U,U]}$
, and since
$H \in \overline {f \circ U} \cap \text {Inv}_{[U,U]}$
, and since
![]() $\triangleleft $
lists members of
$\triangleleft $
lists members of
![]() $\text {Inv}_{[U,U]}$
before members of
$\text {Inv}_{[U,U]}$
before members of
![]() $\text {Inv}_U \setminus \text {Inv}_{[U,U]}$
, it follows that
$\text {Inv}_U \setminus \text {Inv}_{[U,U]}$
, it follows that
![]() $F_{f \circ U} \in \text {Inv}_{[U,U]}$
. So
$F_{f \circ U} \in \text {Inv}_{[U,U]}$
. So
![]() $F_{f \circ U}$
is invariant with respect to some nonidentity member of
$F_{f \circ U}$
is invariant with respect to some nonidentity member of
![]() $[U,U]$
. By Lemma 13 and our assumption that
$[U,U]$
. By Lemma 13 and our assumption that
![]() $[U,U]$
acts freely on
$[U,U]$
acts freely on
![]() $I$
,
$I$
,
![]() $F_{f \circ U}$
is fully
$F_{f \circ U}$
is fully
![]() $\gamma $
-invariant.
$\gamma $
-invariant.
Define
by
 $$ \begin{align} \mathcal{P}(f):= F_{f \circ U}(\underbrace{\varphi^{-1}(t_f)}_{\substack{\text{Right end-} \\ \text{point of} \\ \text{dom}\big( f \circ \varphi \big) }}), \end{align} $$
$$ \begin{align} \mathcal{P}(f):= F_{f \circ U}(\underbrace{\varphi^{-1}(t_f)}_{\substack{\text{Right end-} \\ \text{point of} \\ \text{dom}\big( f \circ \varphi \big) }}), \end{align} $$
where
![]() $\varphi $
is any member of
$\varphi $
is any member of
![]() $U$
witnessing that
$U$
witnessing that
![]() $F_{f \circ U}$
is an element of
$F_{f \circ U}$
is an element of
![]() $\overline {f \circ U}$
, i.e., where
$\overline {f \circ U}$
, i.e., where
![]() $\varphi $
is any member of
$\varphi $
is any member of
![]() $U$
such that
$U$
such that
![]() $F_{f \circ U}$
extends
$F_{f \circ U}$
extends
![]() $f \circ \varphi $
. The next claim says that
$f \circ \varphi $
. The next claim says that
![]() $\mathcal {P}$
is well defined, in the sense that the expression above does not depend on the choice of the
$\mathcal {P}$
is well defined, in the sense that the expression above does not depend on the choice of the
![]() $\varphi $
.
$\varphi $
.
Claim 15 The definition of
![]() $\mathcal {P}(f)$
in (2) does not depend which
$\mathcal {P}(f)$
in (2) does not depend which
![]() $\varphi \in U$
we choose to witness
$\varphi \in U$
we choose to witness
![]() $F_{f \circ U} \in \overline {f \circ U}$
. That is, if
$F_{f \circ U} \in \overline {f \circ U}$
. That is, if
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
are both in
$\varphi _2$
are both in
![]() $U$
, and
$U$
, and
![]() $F_{f \circ U}$
extends both
$F_{f \circ U}$
extends both
![]() $f \circ \varphi _1$
and
$f \circ \varphi _1$
and
![]() $f \circ \varphi _2$
, then
$f \circ \varphi _2$
, then
Proof We follow the proof in [Reference Bajpai and Velleman1, Theorem 5] very closely (which was for the special case where
![]() $I=\mathbb {R}$
and
$I=\mathbb {R}$
and
![]() $U$
was the group of increasing affine functions).
$U$
was the group of increasing affine functions).
For the remainder of the proof of the claim, we abbreviate
![]() $F_{f \circ U}$
by
$F_{f \circ U}$
by
![]() $F$
, and omit the “
$F$
, and omit the “
![]() $\circ $
” symbol in compositions. Let
$\circ $
” symbol in compositions. Let
![]() $x_1=\varphi ^{-1}_1(t_f)$
and
$x_1=\varphi ^{-1}_1(t_f)$
and
![]() $x_2=\varphi ^{-1}_2(t_f)$
; so the domain of
$x_2=\varphi ^{-1}_2(t_f)$
; so the domain of
![]() $f \varphi _1$
is
$f \varphi _1$
is
![]() $(-\infty ,x_1)$
, the domain of
$(-\infty ,x_1)$
, the domain of
![]() $f \varphi _2$
is
$f \varphi _2$
is
![]() $(-\infty ,x_2)$
, and
$(-\infty ,x_2)$
, and
![]() $F$
extends both of them. We must show that
$F$
extends both of them. We must show that
![]() $F(x_1)=F(x_2)$
. Clearly, this holds if
$F(x_1)=F(x_2)$
. Clearly, this holds if
![]() $x_1=x_2$
, so suppose from now on that
$x_1=x_2$
, so suppose from now on that
![]() $x_1 \ne x_2$
. In particular,
$x_1 \ne x_2$
. In particular,
because it moves
![]() $x_2$
to
$x_2$
to
![]() $x_1$
. Since
$x_1$
. Since
![]() $F$
extends
$F$
extends
![]() $f \varphi _1$
before
$f \varphi _1$
before
![]() $x_1$
and extends
$x_1$
and extends
![]() $f \varphi _2$
before
$f \varphi _2$
before
![]() $x_2$
, it follows that:Footnote
11
$x_2$
, it follows that:Footnote
11
Since
![]() $F=F_{f \circ U}$
extends
$F=F_{f \circ U}$
extends
![]() $f \circ \varphi _2$
,
$f \circ \varphi _2$
,
![]() $F$
is
$F$
is
![]() $\varphi _1^{-1} \varphi _2$
-invariant before
$\varphi _1^{-1} \varphi _2$
-invariant before
![]() $\varphi _2^{-1}(t_f)=x_2$
, and both
$\varphi _2^{-1}(t_f)=x_2$
, and both
![]() $\varphi _2$
and
$\varphi _2$
and
![]() $\varphi _1^{-1} \varphi _2$
are in
$\varphi _1^{-1} \varphi _2$
are in
![]() $U$
, part (1) of Claim 14 implies
$U$
, part (1) of Claim 14 implies
So there is some
![]() $\psi \in U$
such that
$\psi \in U$
such that
![]() $\text {id}_I \ne \psi $
and
$\text {id}_I \ne \psi $
and
![]() $F = F \psi $
. Without loss of generality—since both
$F = F \psi $
. Without loss of generality—since both
![]() $\psi $
and
$\psi $
and
![]() $\psi ^{-1}$
are both order-preserving and
$\psi ^{-1}$
are both order-preserving and
![]() $F$
is invariant with respect to both—we can assume that
$F$
is invariant with respect to both—we can assume that
Still following the proof of [Reference Bajpai and Velleman1, Theorem 5], we consider two cases. The assumption that nonidentity members of
![]() $U$
have at most one fixed point is used in Case 1, and the assumption that
$U$
have at most one fixed point is used in Case 1, and the assumption that
![]() $[U,U]$
acts freely on
$[U,U]$
acts freely on
![]() $I$
is used in Case 2.
$I$
is used in Case 2.
Case 1:
![]() $\psi $
commutes with
$\psi $
commutes with
![]() $\varphi _2^{-1} \varphi _1$
. We first claim that
$\varphi _2^{-1} \varphi _1$
. We first claim that
![]() $\psi (x_1) < x_1$
. If not, then by (6),
$\psi (x_1) < x_1$
. If not, then by (6),
![]() $x_1$
is a fixed point of
$x_1$
is a fixed point of
![]() $\psi $
. Then
$\psi $
. Then
 $$\begin{align*}\psi(\underbrace{x_2}_{\varphi_2^{-1} \varphi_1(x_1)}) = \psi \varphi_2^{-1} \varphi_1 (x_1) \overset{\text{by case}}{=} \varphi_2^{-1} \varphi_1 \underbrace{\psi(x_1)}_{x_1} = x_2, \end{align*}$$
$$\begin{align*}\psi(\underbrace{x_2}_{\varphi_2^{-1} \varphi_1(x_1)}) = \psi \varphi_2^{-1} \varphi_1 (x_1) \overset{\text{by case}}{=} \varphi_2^{-1} \varphi_1 \underbrace{\psi(x_1)}_{x_1} = x_2, \end{align*}$$
so
![]() $x_2$
is another fixed point of
$x_2$
is another fixed point of
![]() $\psi $
. This contradicts that nonidentity members of
$\psi $
. This contradicts that nonidentity members of
![]() $U$
have at most one fixed point.
$U$
have at most one fixed point.
So
![]() $\psi (x_1) < x_1$
. Then
$\psi (x_1) < x_1$
. Then
 $$ \begin{align*} F (x_1) & = F \psi (x_1) & \text{ (because }F \text{ is }\psi\text{-invariant)} \\& = F \varphi_2^{-1} \varphi_1 \psi(x_1) & \text{ (because }\psi(x_1) < x_1 \text{ and }(4)) \\ & = F \psi\varphi_2^{-1} \varphi_1(x_1) & (\psi \text{ commutes with }\varphi_2^{-1} \varphi_1 \text{ by the Case)} \\ & = F \psi(x_2) & \\ & = F(x_2) & \text{ (because }F \text{ is }\psi\text{-invariant)}. \end{align*} $$
$$ \begin{align*} F (x_1) & = F \psi (x_1) & \text{ (because }F \text{ is }\psi\text{-invariant)} \\& = F \varphi_2^{-1} \varphi_1 \psi(x_1) & \text{ (because }\psi(x_1) < x_1 \text{ and }(4)) \\ & = F \psi\varphi_2^{-1} \varphi_1(x_1) & (\psi \text{ commutes with }\varphi_2^{-1} \varphi_1 \text{ by the Case)} \\ & = F \psi(x_2) & \\ & = F(x_2) & \text{ (because }F \text{ is }\psi\text{-invariant)}. \end{align*} $$
Case 2:
![]() $\psi $
does not commute with
$\psi $
does not commute with
![]() $\varphi _2^{-1} \varphi _1$
. Let
$\varphi _2^{-1} \varphi _1$
. Let
![]() $\tau := \varphi _2^{-1} \varphi _1$
, and consider the commutator
$\tau := \varphi _2^{-1} \varphi _1$
, and consider the commutator
![]() $\psi ^{-1} \tau \psi \tau ^{-1}$
. By our case,
$\psi ^{-1} \tau \psi \tau ^{-1}$
. By our case,
First, we show that
To see this, first observe that
![]() $\tau (x_1) = x_2$
. Suppose
$\tau (x_1) = x_2$
. Suppose
![]() $z < x_2$
. Then
$z < x_2$
. Then
![]() $\tau ^{-1} (z) < x_1$
, and by (6),
$\tau ^{-1} (z) < x_1$
, and by (6),
![]() $\psi \tau ^{-1}(z) < x_1$
, and hence (since
$\psi \tau ^{-1}(z) < x_1$
, and hence (since
![]() $\tau (x_1) = x_2$
)
$\tau (x_1) = x_2$
)
![]() $\tau \psi \tau ^{-1}(z) < x_2$
. Then
$\tau \psi \tau ^{-1}(z) < x_2$
. Then
 $$ \begin{align*} F \beta (z) & = F \psi^{-1} \tau \psi \tau^{-1}(z) \\ & = F \tau \psi \tau^{-1}(z) & (F \text{ is } \psi\text{-invariant)} \\ & = F \underbrace{\varphi_1^{-1} \varphi_2}_{\tau^{-1}} \tau \psi \tau^{-1}(z) & \text{(by }(4)\text{ and since }\tau \psi \tau^{-1}(z) < x_2) \\ & = F \psi \tau^{-1}(z) & \\ & = F \tau^{-1}(z) & (F \text{ is }\psi\text{-invariant)} \\ & = F \varphi_1^{-1} \varphi_2 (z) & \\ & = F(z) & \text{(by }(4)\text{ and }z < x_2), \end{align*} $$
$$ \begin{align*} F \beta (z) & = F \psi^{-1} \tau \psi \tau^{-1}(z) \\ & = F \tau \psi \tau^{-1}(z) & (F \text{ is } \psi\text{-invariant)} \\ & = F \underbrace{\varphi_1^{-1} \varphi_2}_{\tau^{-1}} \tau \psi \tau^{-1}(z) & \text{(by }(4)\text{ and since }\tau \psi \tau^{-1}(z) < x_2) \\ & = F \psi \tau^{-1}(z) & \\ & = F \tau^{-1}(z) & (F \text{ is }\psi\text{-invariant)} \\ & = F \varphi_1^{-1} \varphi_2 (z) & \\ & = F(z) & \text{(by }(4)\text{ and }z < x_2), \end{align*} $$
which concludes the proof of (8). By (7), (8), and part (2) of Claim 14,
Since
![]() $\text {id} \ne \beta \in [U,U]$
and
$\text {id} \ne \beta \in [U,U]$
and
![]() $[U,U]$
acts freely on
$[U,U]$
acts freely on
![]() $I$
, in particular,
$I$
, in particular,
![]() $x_2$
is not a fixed point of
$x_2$
is not a fixed point of
![]() $\beta $
. Let
$\beta $
. Let
![]() $\alpha $
denote whichever one of
$\alpha $
denote whichever one of
![]() $\beta $
,
$\beta $
,
![]() $\beta ^{-1}$
sends
$\beta ^{-1}$
sends
![]() $x_2$
to an output strictly less than
$x_2$
to an output strictly less than
![]() $x_2$
. Then:
$x_2$
. Then:
Next, we claim that
Suppose
![]() $z < x_1$
. Then
$z < x_1$
. Then
 $$ \begin{align*} F \tau^{-1} \alpha \tau(z) & = F \varphi_1^{-1} \varphi_2 \underbrace{\alpha \overbrace{\varphi_2^{-1} \varphi_1 (z)}^{<x_2}}_{\substack{<x_2 \text{ because } \\ \alpha(x_2) \le x_2 }} & \\ & = F \alpha \varphi_2^{-1} \varphi_1(z) & \text{ by }(4) \\ & = F \varphi_2^{-1} \varphi_1(z) & (F \text{ is } \alpha\text{-invariant)} \\ & = F(z) & \text{by }(4)\text{ and }z < x_1, \end{align*} $$
$$ \begin{align*} F \tau^{-1} \alpha \tau(z) & = F \varphi_1^{-1} \varphi_2 \underbrace{\alpha \overbrace{\varphi_2^{-1} \varphi_1 (z)}^{<x_2}}_{\substack{<x_2 \text{ because } \\ \alpha(x_2) \le x_2 }} & \\ & = F \alpha \varphi_2^{-1} \varphi_1(z) & \text{ by }(4) \\ & = F \varphi_2^{-1} \varphi_1(z) & (F \text{ is } \alpha\text{-invariant)} \\ & = F(z) & \text{by }(4)\text{ and }z < x_1, \end{align*} $$
which concludes the proof of (11).
Recall that commutator subgroups are always normal; hence,
![]() $\tau ^{-1} \alpha \tau $
is an element of
$\tau ^{-1} \alpha \tau $
is an element of
![]() $[U,U]$
. Then, by (11), the fact that
$[U,U]$
. Then, by (11), the fact that
![]() $F$
extends
$F$
extends
![]() $f \varphi _1$
, and since
$f \varphi _1$
, and since
![]() $\varphi _1 \in U$
and
$\varphi _1 \in U$
and
![]() $\tau ^{-1} \alpha \tau \in [U,U]$
, part (2) of Claim 14 ensures that
$\tau ^{-1} \alpha \tau \in [U,U]$
, part (2) of Claim 14 ensures that
Finally,
 $$ \begin{align*} F(x_1) & =F \tau^{-1} \underbrace{\alpha \overbrace{\tau (x_1)}^{x_2}}_{<x_2 \text{ by (10)}} & \text{by }(12) \\ & = F \alpha \tau (x_1)& \text{ by }(4) \\ & = F \tau(x_1) & F \text{ is }\alpha\text{-invariant} \\ & = F(x_2).\\[-32pt] & \end{align*} $$
$$ \begin{align*} F(x_1) & =F \tau^{-1} \underbrace{\alpha \overbrace{\tau (x_1)}^{x_2}}_{<x_2 \text{ by (10)}} & \text{by }(12) \\ & = F \alpha \tau (x_1)& \text{ by }(4) \\ & = F \tau(x_1) & F \text{ is }\alpha\text{-invariant} \\ & = F(x_2).\\[-32pt] & \end{align*} $$
With Claim 15 in hand, we can now finish the proof of Theorem 5. To see the
![]() $U$
-anonymity of
$U$
-anonymity of
![]() $\mathcal {P}$
, suppose
$\mathcal {P}$
, suppose
![]() $f,g \in {}^{\underset {\smile }{I}} S$
,
$f,g \in {}^{\underset {\smile }{I}} S$
,
![]() $\tau \in U$
,
$\tau \in U$
,
![]() $\tau (t_g) = t_f$
, and
$\tau (t_g) = t_f$
, and
![]() $g = f \circ \tau $
. Then
$g = f \circ \tau $
. Then
![]() $g \in f \circ U$
, and it follows that
$g \in f \circ U$
, and it follows that
![]() $f \circ U = g \circ U$
and hence
$f \circ U = g \circ U$
and hence
Let
![]() $F$
denote this common function. Let
$F$
denote this common function. Let
![]() $\varphi \in U$
witness that
$\varphi \in U$
witness that
![]() $F \in \overline {g \circ U}$
; i.e.,
$F \in \overline {g \circ U}$
; i.e.,
![]() $F$
extends
$F$
extends
![]() $g \circ \varphi = f \circ \tau \circ \varphi $
. So
$g \circ \varphi = f \circ \tau \circ \varphi $
. So
![]() $F = F_{f \circ U}$
extends
$F = F_{f \circ U}$
extends
![]() $f \circ (\tau \circ \varphi )$
, and since
$f \circ (\tau \circ \varphi )$
, and since
![]() $\tau \circ \varphi \in U$
, Claim 15 ensures that
$\tau \circ \varphi \in U$
, Claim 15 ensures that
![]() $\mathcal {P}(f) = F\Big ( (\tau \circ \varphi )^{-1}(t_f) \Big )$
. Then
$\mathcal {P}(f) = F\Big ( (\tau \circ \varphi )^{-1}(t_f) \Big )$
. Then
 $$ \begin{align} \mathcal{P}(g) = F \big( \varphi^{-1}(\underbrace{t_g}_{\tau^{-1}(t_f)}) \big) = F\Big( (\tau \circ \varphi)^{-1} (t_f) \Big)= \mathcal{P}(f). \end{align} $$
$$ \begin{align} \mathcal{P}(g) = F \big( \varphi^{-1}(\underbrace{t_g}_{\tau^{-1}(t_f)}) \big) = F\Big( (\tau \circ \varphi)^{-1} (t_f) \Big)= \mathcal{P}(f). \end{align} $$
To see that
![]() $\mathcal {P}$
is good (this argument first appeared in Hardin–Taylor [Reference Hardin and Taylor5]), suppose
$\mathcal {P}$
is good (this argument first appeared in Hardin–Taylor [Reference Hardin and Taylor5]), suppose
![]() $H: I \to S$
. Let
$H: I \to S$
. Let
By Fact 9 (from page 5), to see that
![]() $B$
has measure zero—in fact, is countable and nowhere dense—it suffices to show that
$B$
has measure zero—in fact, is countable and nowhere dense—it suffices to show that
![]() $B$
is a wellordered subset of
$B$
is a wellordered subset of
![]() $\mathbb {R}$
under the usual ordering
$\mathbb {R}$
under the usual ordering
![]() $<$
on
$<$
on
![]() $\mathbb {R}$
; and for that it suffices to find an order-preserving embedding from
$\mathbb {R}$
; and for that it suffices to find an order-preserving embedding from
![]() $(B,<)$
into
$(B,<)$
into
![]() $\left ( {}^I S, \triangleleft \right )$
.Footnote
12
Define
$\left ( {}^I S, \triangleleft \right )$
.Footnote
12
Define
To see that
![]() $e$
is order-preserving, suppose
$e$
is order-preserving, suppose
![]() $s < t$
are both in
$s < t$
are both in
![]() $B$
; we will show that
$B$
; we will show that
![]() $e(s) \triangleleft e(t)$
by showing
$e(s) \triangleleft e(t)$
by showing
![]() $e(s) \trianglelefteq e(t)$
and
$e(s) \trianglelefteq e(t)$
and
![]() $e(s) \ne e(t)$
. We first prove the nonstrict inequality, i.e., that
$e(s) \ne e(t)$
. We first prove the nonstrict inequality, i.e., that
Since
![]() $F_{ H|_{(-\infty ,s)} \circ U}$
is, by definition, the
$F_{ H|_{(-\infty ,s)} \circ U}$
is, by definition, the
![]() $\triangleleft $
-least member of
$\triangleleft $
-least member of
![]() $\overline {H|_{(-\infty ,s)} \circ U} $
, it suffices to show that
$\overline {H|_{(-\infty ,s)} \circ U} $
, it suffices to show that
Now,
![]() $F_{ H|_{(-\infty ,t)} \circ U}$
, being a member of
$F_{ H|_{(-\infty ,t)} \circ U}$
, being a member of
![]() $\overline {H|_{(-\infty ,t)} \circ U}$
, extends
$\overline {H|_{(-\infty ,t)} \circ U}$
, extends
![]() $H|_{(-\infty ,t)} \circ \varphi $
for some
$H|_{(-\infty ,t)} \circ \varphi $
for some
![]() $\varphi \in U$
. However, since
$\varphi \in U$
. However, since
![]() $s < t$
(and
$s < t$
(and
![]() $\varphi $
is order-preserving), it also extends
$\varphi $
is order-preserving), it also extends
![]() $H|_{(-\infty ,s)} \circ \varphi $
. This verifies (15).
$H|_{(-\infty ,s)} \circ \varphi $
. This verifies (15).
To prove that
suppose toward a contradiction that they are equal; let
![]() $F$
denote the common function. Let
$F$
denote the common function. Let
![]() $\varphi \in U$
witness that
$\varphi \in U$
witness that
![]() $F \in \overline {H|_{(-\infty ,t)} \circ U}$
; so
$F \in \overline {H|_{(-\infty ,t)} \circ U}$
; so
![]() $F$
extends
$F$
extends
![]() $H|_{(-\infty ,t)} \circ \varphi $
. Since
$H|_{(-\infty ,t)} \circ \varphi $
. Since
![]() $s < t$
and
$s < t$
and
![]() $\varphi $
is order-preserving,
$\varphi $
is order-preserving,
![]() $F$
also extends
$F$
also extends
![]() $H|_{(-\infty ,s)} \circ \varphi $
. Then, by Claim 15 and the fact that
$H|_{(-\infty ,s)} \circ \varphi $
. Then, by Claim 15 and the fact that
![]() $F = F_{H|_{(-\infty ,s)} \circ U}$
,
$F = F_{H|_{(-\infty ,s)} \circ U}$
,
Now, the left side of (16) is not equal to
![]() $H(s)$
, because
$H(s)$
, because
![]() $s \in B$
. So,
$s \in B$
. So,
On the other hand,
![]() $F$
extends
$F$
extends
![]() $H|_{(-\infty ,t)} \circ \varphi $
, whose domain is
$H|_{(-\infty ,t)} \circ \varphi $
, whose domain is
![]() $(-\infty , \varphi ^{-1}(t))$
; and since
$(-\infty , \varphi ^{-1}(t))$
; and since
![]() $s < t$
and
$s < t$
and
![]() $\varphi $
(and hence
$\varphi $
(and hence
![]() $\varphi ^{-1}$
) is order-preserving,
$\varphi ^{-1}$
) is order-preserving,
![]() $\varphi ^{-1}(s) < \varphi ^{-1}(t)$
. So
$\varphi ^{-1}(s) < \varphi ^{-1}(t)$
. So
![]() $F$
and
$F$
and
![]() $H|_{(-\infty ,t)} \circ \varphi $
agree on the input
$H|_{(-\infty ,t)} \circ \varphi $
agree on the input
![]() $\varphi ^{-1}(s)$
. Then
$\varphi ^{-1}(s)$
. Then
![]() $F\big (\varphi ^{-1}(s)\big ) = H|_{(-\infty ,t)} \circ \varphi \big ( \varphi ^{-1}(s) \big ) = H\big ( \varphi (\varphi ^{-1}(s)) \big ) = H(s)$
, contradicting (17).
$F\big (\varphi ^{-1}(s)\big ) = H|_{(-\infty ,t)} \circ \varphi \big ( \varphi ^{-1}(s) \big ) = H\big ( \varphi (\varphi ^{-1}(s)) \big ) = H(s)$
, contradicting (17).
This concludes the proof of Theorem 5.
4 Proof of Corollary 6
In this section, we prove parts (C) and (E) of Corollary 6. The remaining parts should be clear. The following lemma proves part (C).
Lemma 16 Suppose
![]() $U$
is a subgroup of
$U$
is a subgroup of
![]() $\mathrm{Homeo}^+(I)$
,
$\mathrm{Homeo}^+(I)$
,
![]() $U$
acts transitively on
$U$
acts transitively on
![]() $I$
,
$I$
,
![]() $[U,U]$
acts freely on
$[U,U]$
acts freely on
![]() $I$
, and each nonidentity member of
$I$
, and each nonidentity member of
![]() $U$
has only finitely many fixed points. Then, in fact, each nonidentity member of
$U$
has only finitely many fixed points. Then, in fact, each nonidentity member of
![]() $U$
has at most one fixed point.
$U$
has at most one fixed point.
Proof Suppose toward a contradiction that there is some nonidentity
![]() $\varphi \in I$
and some
$\varphi \in I$
and some
![]() $x_1 < x_2$
in
$x_1 < x_2$
in
![]() $I$
such that both
$I$
such that both
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are fixed points of
$x_2$
are fixed points of
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $U$
acts transitively on
$U$
acts transitively on
![]() $I$
, there is some
$I$
, there is some
![]() $\tau \in U$
such that
$\tau \in U$
such that
![]() $\tau (x_1) = x_2$
. Then
$\tau (x_1) = x_2$
. Then
![]() $x_2$
is a fixed point of
$x_2$
is a fixed point of
![]() $\tau \varphi \tau ^{-1} \varphi ^{-1}$
. We claim that
$\tau \varphi \tau ^{-1} \varphi ^{-1}$
. We claim that
![]() $\tau \varphi \tau ^{-1} \varphi ^{-1} \ne \text {id}_I$
, which will contradict the assumption that
$\tau \varphi \tau ^{-1} \varphi ^{-1} \ne \text {id}_I$
, which will contradict the assumption that
![]() $[U,U]$
acts freely on
$[U,U]$
acts freely on
![]() $I$
.
$I$
.
Suppose toward a contradiction that
![]() $\tau \varphi \tau ^{-1} \varphi ^{-1} = \text {id}_I$
; i.e., that
$\tau \varphi \tau ^{-1} \varphi ^{-1} = \text {id}_I$
; i.e., that
For
![]() $n \ge 3$
, set
$n \ge 3$
, set
![]() $x_n:= \tau (x_{n-1})$
. Since
$x_n:= \tau (x_{n-1})$
. Since
![]() $\tau $
is increasing and
$\tau $
is increasing and
![]() $\tau (x_1) = x_2$
, the sequence
$\tau (x_1) = x_2$
, the sequence
![]() $(x_n)_n$
is a strictly increasing sequence in
$(x_n)_n$
is a strictly increasing sequence in
![]() $I$
. We prove by induction that each
$I$
. We prove by induction that each
![]() $x_n$
is a fixed point of
$x_n$
is a fixed point of
![]() $\varphi $
, which will contradict that
$\varphi $
, which will contradict that
![]() $\varphi $
has only finitely many fixed points. That
$\varphi $
has only finitely many fixed points. That
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are fixed points is by assumption. Now, if
$x_2$
are fixed points is by assumption. Now, if
![]() $x_n$
is a fixed point of
$x_n$
is a fixed point of
![]() $\varphi $
, then
$\varphi $
, then
 $$ \begin{align*} \varphi(x_{n+1}) & = \tau \varphi \tau^{-1} (x_{n+1}) & \text{by }(18) \\ &= \tau \varphi \tau^{-1} \big( \tau(x_n) \big) & \text{definition of }x_{n+1} \\ & = \tau \varphi(x_n) & \\ & = \tau(x_n) & \text{Induction Hypothesis} \\ & = x_{n+1}.\\[-32pt] \end{align*} $$
$$ \begin{align*} \varphi(x_{n+1}) & = \tau \varphi \tau^{-1} (x_{n+1}) & \text{by }(18) \\ &= \tau \varphi \tau^{-1} \big( \tau(x_n) \big) & \text{definition of }x_{n+1} \\ & = \tau \varphi(x_n) & \\ & = \tau(x_n) & \text{Induction Hypothesis} \\ & = x_{n+1}.\\[-32pt] \end{align*} $$
The “at most one” in the conclusion of Lemma 16 is best possible, since when
![]() $I=\mathbb {R}$
and
$I=\mathbb {R}$
and
![]() $U$
is the group of increasing affine functions, the commutator subgroup
$U$
is the group of increasing affine functions, the commutator subgroup
![]() $[U,U]$
is exactly the group of shift functions (i.e., affine functions of slope 1). And in that case,
$[U,U]$
is exactly the group of shift functions (i.e., affine functions of slope 1). And in that case,
![]() $U$
acts transitively on
$U$
acts transitively on
![]() $\mathbb {R}$
,
$\mathbb {R}$
,
![]() $[U,U]$
acts freely on
$[U,U]$
acts freely on
![]() $\mathbb {R}$
, and members of
$\mathbb {R}$
, and members of
![]() $U \setminus [U,U]$
have exactly one fixed point.
$U \setminus [U,U]$
have exactly one fixed point.
Next, we prove part (E) of Corollary 6. Suppose
![]() $\varphi \in \mathrm{Homeo}^+(I)$
, and that the set
$\varphi \in \mathrm{Homeo}^+(I)$
, and that the set
![]() $C$
of fixed points of
$C$
of fixed points of
![]() $\varphi $
has Lebesgue measure zero. Since
$\varphi $
has Lebesgue measure zero. Since
![]() $\varphi $
is continuous,
$\varphi $
is continuous,
![]() $C$
is closed. For
$C$
is closed. For
![]() $t \in I \setminus C$
, let
$t \in I \setminus C$
, let
![]() $a(t)$
denote the largest member of
$a(t)$
denote the largest member of
![]() $C \cap (-\infty ,t)$
if that intersection is nonempty; otherwise, set
$C \cap (-\infty ,t)$
if that intersection is nonempty; otherwise, set
![]() $a(t)=-\infty $
. Closure of
$a(t)=-\infty $
. Closure of
![]() $C$
, together with the assumption that
$C$
, together with the assumption that
![]() $t \notin C$
, ensures
$t \notin C$
, ensures
![]() $a(t)$
is well defined. Similarly, let
$a(t)$
is well defined. Similarly, let
![]() $b(t)$
be the smallest element of
$b(t)$
be the smallest element of
![]() $C \cap (t,\infty )$
if that intersection is nonempty, and
$C \cap (t,\infty )$
if that intersection is nonempty, and
![]() $b(t)=+\infty $
otherwise. Finally, if
$b(t)=+\infty $
otherwise. Finally, if
![]() $t \in I \setminus C$
, set
$t \in I \setminus C$
, set
![]() $J(t):= \big ( a(t), b(t) \big )$
.
$J(t):= \big ( a(t), b(t) \big )$
.
Let
and notice
![]() $\mathcal {J}$
is a pairwise disjoint collection of open intervals; hence,
$\mathcal {J}$
is a pairwise disjoint collection of open intervals; hence,
Furthermore, for each
![]() $J \in \mathcal {J}$
,
$J \in \mathcal {J}$
,
![]() $\varphi |_{J}$
is an element of
$\varphi |_{J}$
is an element of
![]() $\mathrm{Homeo}^+(J)$
, and moreover is fixed-point-free, since
$\mathrm{Homeo}^+(J)$
, and moreover is fixed-point-free, since
![]() $J=(a(t),b(t))$
for some
$J=(a(t),b(t))$
for some
![]() $t \in I \setminus C$
, and
$t \in I \setminus C$
, and
![]() $C \cap (a(t),b(t))$
is empty. The following claim is a basic application of the Intermediate Value Theorem.
$C \cap (a(t),b(t))$
is empty. The following claim is a basic application of the Intermediate Value Theorem.
Claim 17 Each nonidentity member of
![]() $\langle \varphi \rangle $
has the same fixed points as
$\langle \varphi \rangle $
has the same fixed points as
![]() $\varphi $
.
$\varphi $
.
Proof Suppose
![]() $\tau $
is a nonidentity member of
$\tau $
is a nonidentity member of
![]() $\langle \varphi \rangle $
; then
$\langle \varphi \rangle $
; then
![]() $\tau = \varphi ^n$
for some nonzero
$\tau = \varphi ^n$
for some nonzero
![]() $n \in \mathbb {Z}$
. Clearly, every fixed point of
$n \in \mathbb {Z}$
. Clearly, every fixed point of
![]() $\varphi $
is also a fixed point of
$\varphi $
is also a fixed point of
![]() $\tau $
. Now, suppose
$\tau $
. Now, suppose
![]() $t \in I$
is not a fixed point of
$t \in I$
is not a fixed point of
![]() $\varphi $
. Consider the interval
$\varphi $
. Consider the interval
![]() $J:=(a(t), b(t))$
and the restriction
$J:=(a(t), b(t))$
and the restriction
![]() $\varphi |_J$
. Since
$\varphi |_J$
. Since
![]() $\varphi |_J$
has no fixed points in
$\varphi |_J$
has no fixed points in
![]() $J$
, the Intermediate Value Theorem implies that either
$J$
, the Intermediate Value Theorem implies that either
![]() $\varphi (x) < x$
for all
$\varphi (x) < x$
for all
![]() $x \in J$
, or
$x \in J$
, or
![]() $\varphi (x)> x$
for all
$\varphi (x)> x$
for all
![]() $x \in J$
. In the former case, since
$x \in J$
. In the former case, since
![]() $\varphi $
is order-preserving, it follows by induction that
$\varphi $
is order-preserving, it follows by induction that
![]() $\varphi ^n(x) < x$
and
$\varphi ^n(x) < x$
and
![]() $\varphi ^{-n}(x)> x$
for all
$\varphi ^{-n}(x)> x$
for all
![]() $n \in \mathbb {N}$
and all
$n \in \mathbb {N}$
and all
![]() $x \in J$
(and similarly for the latter case, with inequalities reversed). In particular,
$x \in J$
(and similarly for the latter case, with inequalities reversed). In particular,
![]() $t$
is not a fixed point of
$t$
is not a fixed point of
![]() $\tau $
.
$\tau $
.
Suppose
![]() $J \in \mathcal {J}$
. Since
$J \in \mathcal {J}$
. Since
![]() $\varphi |_J$
is fixed-point-free, Claim 17 ensures that the cyclic subgroup
$\varphi |_J$
is fixed-point-free, Claim 17 ensures that the cyclic subgroup
![]() $\langle \varphi |_J \rangle $
generated by
$\langle \varphi |_J \rangle $
generated by
![]() $\varphi |_J$
in
$\varphi |_J$
in
![]() $\mathrm{Homeo}^+(J)$
acts freely on
$\mathrm{Homeo}^+(J)$
acts freely on
![]() $J$
. So, by Theorem 5, there exists a good,
$J$
. So, by Theorem 5, there exists a good,
![]() $\langle \varphi |_J \rangle $
-anonymous predictor
$\langle \varphi |_J \rangle $
-anonymous predictor
![]() $\mathcal {P}_J$
for functions in
$\mathcal {P}_J$
for functions in
![]() ${}^J S$
. Define
${}^J S$
. Define
as follows: fix any
![]() $s_0 \in S$
. Given
$s_0 \in S$
. Given
![]() $f: (-\infty , t_f) \to S$
, consider cases:
$f: (-\infty , t_f) \to S$
, consider cases:
-
• If
 $t_f \in C$
, let
$t_f \in C$
, let
 $\mathcal {Q}(f):= s_0$
.
$\mathcal {Q}(f):= s_0$
. -
• If
 $t_f \notin C$
, define
$t_f \notin C$
, define
 $\mathcal {Q}(f):= \mathcal {P}_{J(t_f)} \Big ( f|_{J(t_f)} \Big )$
; note that the domain of
$\mathcal {Q}(f):= \mathcal {P}_{J(t_f)} \Big ( f|_{J(t_f)} \Big )$
; note that the domain of
 $f|_{J(t_f)}$
is
$f|_{J(t_f)}$
is
 $J(t_f) \cap (-\infty , t_f) = \big ( a(t_f), t_f \big )$
.
$J(t_f) \cap (-\infty , t_f) = \big ( a(t_f), t_f \big )$
.
To see that
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $\langle \varphi \rangle $
-anonymous, consider any
$\langle \varphi \rangle $
-anonymous, consider any
![]() $f:(-\infty ,t_f) \to S$
and any nonidentity
$f:(-\infty ,t_f) \to S$
and any nonidentity
![]() $\tau \in \langle \varphi \rangle $
. We need to show that
$\tau \in \langle \varphi \rangle $
. We need to show that
![]() $\mathcal {Q}(f) = \mathcal {Q}\big ( f \tau \big )$
. If
$\mathcal {Q}(f) = \mathcal {Q}\big ( f \tau \big )$
. If
![]() $t_f \in C$
, then by the claim,
$t_f \in C$
, then by the claim,
![]() $t_f$
is a fixed point of both
$t_f$
is a fixed point of both
![]() $\varphi $
and
$\varphi $
and
![]() $\tau $
, and hence
$\tau $
, and hence
![]() $t_f = \tau ^{-1}(t_f)$
is the right endpoint of the domain of
$t_f = \tau ^{-1}(t_f)$
is the right endpoint of the domain of
![]() $f \tau $
. So, by definition of
$f \tau $
. So, by definition of
![]() $\mathcal {Q}$
,
$\mathcal {Q}$
,
![]() $\mathcal {Q}(f) = s_0 = \mathcal {Q}(f \tau )$
. If
$\mathcal {Q}(f) = s_0 = \mathcal {Q}(f \tau )$
. If
![]() $t_f \notin C$
, then since
$t_f \notin C$
, then since
![]() $a(t_f)$
and
$a(t_f)$
and
![]() $b(t_f)$
are fixed points of
$b(t_f)$
are fixed points of
![]() $\tau $
,
$\tau $
,
![]() $\tau ^{-1}(t_f)$
is an element of
$\tau ^{-1}(t_f)$
is an element of
![]() $ J(t_f)$
. In particular,
$ J(t_f)$
. In particular,
Then
 $$ \begin{align*} \mathcal{Q} (f) & = \mathcal{P}_{J}\Big( f|_{J} \Big) & \text{(definition of }\mathcal{Q})\\ & = \mathcal{P}_{J}\Big( f|_{J} \ \tau|_{J} \Big) & \text{(by }\langle \varphi|_{J} \rangle\text{-anonymity of }\mathcal{P}_{J}) \\ & = \mathcal{P}_J \Big( (f\tau)_J \Big) & \text{(by }(20)) \\ & = \mathcal{Q}\big( f \tau \big) & \text{(by definition of }\mathcal{Q}, \text{ since }\tau^{-1}(t_f) \notin C). \end{align*} $$
$$ \begin{align*} \mathcal{Q} (f) & = \mathcal{P}_{J}\Big( f|_{J} \Big) & \text{(definition of }\mathcal{Q})\\ & = \mathcal{P}_{J}\Big( f|_{J} \ \tau|_{J} \Big) & \text{(by }\langle \varphi|_{J} \rangle\text{-anonymity of }\mathcal{P}_{J}) \\ & = \mathcal{P}_J \Big( (f\tau)_J \Big) & \text{(by }(20)) \\ & = \mathcal{Q}\big( f \tau \big) & \text{(by definition of }\mathcal{Q}, \text{ since }\tau^{-1}(t_f) \notin C). \end{align*} $$
To see that
![]() $\mathcal {Q}$
is good, fix any
$\mathcal {Q}$
is good, fix any
![]() $H: I \to S$
, and let
$H: I \to S$
, and let
Now,
![]() $B = (B \cap C) \cup (B \setminus C)$
, so it suffices to show that each set in the union is null. Since
$B = (B \cap C) \cup (B \setminus C)$
, so it suffices to show that each set in the union is null. Since
![]() $C$
is null by assumption,
$C$
is null by assumption,
![]() $B \cap C$
is null; so it remains to show that
$B \cap C$
is null; so it remains to show that
![]() $B \setminus C$
is also null. Now,
$B \setminus C$
is also null. Now,
Moreover, by the way we defined
![]() $\mathcal {Q}$
,
$\mathcal {Q}$
,
![]() $B \cap J$
is exactly the set of
$B \cap J$
is exactly the set of
![]() $t \in J$
where
$t \in J$
where
![]() $\mathcal {P}_J\big ( H|_{J \cap (-\infty , t)} \big ) \ne H(t)$
, which has measure zero because
$\mathcal {P}_J\big ( H|_{J \cap (-\infty , t)} \big ) \ne H(t)$
, which has measure zero because
![]() $\mathcal {P}_J$
is good. Together with (19), this implies that the right side of (21) has measure zero.
$\mathcal {P}_J$
is good. Together with (19), this implies that the right side of (21) has measure zero.
Remark 18 Suppose
![]() $U \le \mathrm{Homeo}^+(I)$
, and there is a
$U \le \mathrm{Homeo}^+(I)$
, and there is a
![]() $C \subset I$
such that
$C \subset I$
such that
![]() $C$
is closed (in
$C$
is closed (in
![]() $I$
),
$I$
),
![]() $C$
has measure zero, and each member of
$C$
has measure zero, and each member of
![]() $C$
is a fixed point of every member of
$C$
is a fixed point of every member of
![]() $U$
. Closure of
$U$
. Closure of
![]() $C$
ensures that we can define
$C$
ensures that we can define
![]() $\mathcal {J}=\left \{ \big (a(t),b(t)\big ) \ : \ t \in I \setminus C \right \}$
as in the proof above. Then, for each
$\mathcal {J}=\left \{ \big (a(t),b(t)\big ) \ : \ t \in I \setminus C \right \}$
as in the proof above. Then, for each
![]() $J \in \mathcal {J}$
and
$J \in \mathcal {J}$
and
![]() $\varphi \in U$
,
$\varphi \in U$
,
![]() $\varphi |_J$
is a member of
$\varphi |_J$
is a member of
![]() $\mathrm{Homeo}^+(J)$
, and
$\mathrm{Homeo}^+(J)$
, and
![]() $U_J:= \{ \varphi |_{J} \ : \ \varphi \in U \}$
is a subgroup of
$U_J:= \{ \varphi |_{J} \ : \ \varphi \in U \}$
is a subgroup of
![]() $\mathrm{Homeo}^+(J)$
. If there exists a good,
$\mathrm{Homeo}^+(J)$
. If there exists a good,
![]() $U_J$
-anonymous predictor for every
$U_J$
-anonymous predictor for every
![]() $J \in \mathcal {J}$
, then an argument similar to the one above allows us to amalgamate them to yield a good,
$J \in \mathcal {J}$
, then an argument similar to the one above allows us to amalgamate them to yield a good,
![]() $U$
-anonymous predictor for functions on
$U$
-anonymous predictor for functions on
![]() $I$
.
$I$
.
5 Proof of Theorem 8
In this section, we prove Theorem 8, which strengthens Bajpai–Velleman’s Theorem 4. We remark that their proof actually showed something a bit stronger than is stated in Theorem 4 (or in their paper). Namely, their set
![]() $S=\mathbb {R}/\sim $
had the property that there is no good
$S=\mathbb {R}/\sim $
had the property that there is no good
![]() $S$
-predictor that is anonymous with respect to the class
$S$
-predictor that is anonymous with respect to the class
where
![]() $C^\infty _{\text {Lipschitz}}$
is the set of
$C^\infty _{\text {Lipschitz}}$
is the set of
![]() $f \in C^\infty $
such that for all
$f \in C^\infty $
such that for all
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
![]() $f^{(k)}$
is bounded.
$f^{(k)}$
is bounded.
We strengthen their result in two ways:
-
(1) We show that their result still holds when the class (22) is replaced by the smaller class
 $D^\infty _{\text {Lipschitz}}$
of infinitely Lipschitz diffeomorphisms; i.e., the set of invertible
$D^\infty _{\text {Lipschitz}}$
of infinitely Lipschitz diffeomorphisms; i.e., the set of invertible
 $f: \mathbb {R} \to \mathbb {R}$
such that both
$f: \mathbb {R} \to \mathbb {R}$
such that both
 $f$
and
$f$
and
 $f^{-1}$
are
$f^{-1}$
are
 $C^\infty $
functions, and for every
$C^\infty $
functions, and for every
 $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
 $f^{(k)}$
and
$f^{(k)}$
and
 $(f^{-1})^{(k)}$
are bounded.
$(f^{-1})^{(k)}$
are bounded. -
(2) We show that even a weaker kind of prediction fails.
We first describe the weaker kind of prediction. Given a set
![]() $S$
, let
$S$
, let
![]() $\boldsymbol {{}^{\mathbb {R}^{\circ }} S}$
denote the set of
$\boldsymbol {{}^{\mathbb {R}^{\circ }} S}$
denote the set of
![]() $S$
-valued functions
$S$
-valued functions
![]() $f$
such that
$f$
such that
![]() $\text {dom}(f) = \mathbb {R} \setminus \{ h_f \}$
for some
$\text {dom}(f) = \mathbb {R} \setminus \{ h_f \}$
for some
![]() $h_f \in \mathbb {R}$
(so the domain of
$h_f \in \mathbb {R}$
(so the domain of
![]() $f$
is the reals with a hole at
$f$
is the reals with a hole at
![]() $h_f$
). If
$h_f$
). If
![]() $F$
is a total function on
$F$
is a total function on
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $x \in \mathbb {R}$
,
$x \in \mathbb {R}$
,
![]() $F \setminus \{ x \}$
will denote the restriction of
$F \setminus \{ x \}$
will denote the restriction of
![]() $F$
to the domain
$F$
to the domain
![]() $\mathbb {R} \setminus \{x \}$
. A weak S-predictor will refer to any function
$\mathbb {R} \setminus \{x \}$
. A weak S-predictor will refer to any function
and it will be called a good weak
![]() $S$
-predictor if for every total
$S$
-predictor if for every total
![]() $F: \mathbb {R} \to S$
, the set
$F: \mathbb {R} \to S$
, the set
has Lebesgue measure zero. Roughly,
![]() $\mathcal {P}$
almost always “predicts”
$\mathcal {P}$
almost always “predicts”
![]() $F(x)$
based on the past and future behavior of
$F(x)$
based on the past and future behavior of
![]() $F$
.
$F$
.
Every good
![]() $S$
-predictor yields a good weak
$S$
-predictor yields a good weak
![]() $S$
-predictor, because if
$S$
-predictor, because if
![]() $\mathcal {P}$
is a good
$\mathcal {P}$
is a good
![]() $S$
-predictor, define
$S$
-predictor, define
![]() $\mathcal {Q}$
on
$\mathcal {Q}$
on
![]() ${}^{\mathbb {R}^{\circ }} S$
as follows: given any
${}^{\mathbb {R}^{\circ }} S$
as follows: given any
![]() $f \in {}^{\mathbb {R}^{\circ }} S$
whose domain has a hole at
$f \in {}^{\mathbb {R}^{\circ }} S$
whose domain has a hole at
![]() $h_f$
, define
$h_f$
, define
Then, for any total
![]() $F: \mathbb {R} \to S$
, we have
$F: \mathbb {R} \to S$
, we have
![]() $\mathcal {Q}\Big ( F \setminus \{ x \} \Big ) = \mathcal {P} \Big ( F \restriction (-\infty ,x) \Big )$
, which can only fail to equal
$\mathcal {Q}\Big ( F \setminus \{ x \} \Big ) = \mathcal {P} \Big ( F \restriction (-\infty ,x) \Big )$
, which can only fail to equal
![]() $F(x)$
on a measure zero set.
$F(x)$
on a measure zero set.
If
![]() $U \subseteq \mathrm{Homeo}^+(\mathbb {R})$
, let us say that a weak
$U \subseteq \mathrm{Homeo}^+(\mathbb {R})$
, let us say that a weak
![]() $S$
-predictor
$S$
-predictor
![]() $\mathcal {P}$
is
$\mathcal {P}$
is
![]() $\boldsymbol {U}$
-anonymous if whenever
$\boldsymbol {U}$
-anonymous if whenever
![]() $f,g \in {}^{\mathbb {R}^{\circ }} S$
(with holes
$f,g \in {}^{\mathbb {R}^{\circ }} S$
(with holes
![]() $h_f$
,
$h_f$
,
![]() $h_g$
in their respective domains),
$h_g$
in their respective domains),
![]() $\varphi \in U$
,
$\varphi \in U$
,
![]() $\varphi (h_f) = h_g$
, and
$\varphi (h_f) = h_g$
, and
![]() $f = g \circ \varphi \restriction \left ( \mathbb {R} \setminus \{ h_f \} \right )$
, then
$f = g \circ \varphi \restriction \left ( \mathbb {R} \setminus \{ h_f \} \right )$
, then
![]() $\mathcal {P}(f) = \mathcal {P}(g)$
. Similarly, as above, any good
$\mathcal {P}(f) = \mathcal {P}(g)$
. Similarly, as above, any good
![]() $U$
-anonymous
$U$
-anonymous
![]() $S$
-predictor yields a good
$S$
-predictor yields a good
![]() $U$
-anonymous weak
$U$
-anonymous weak
![]() $S$
-predictor.
$S$
-predictor.
Our goal is to prove the following theorem.
Theorem 19 There is an equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $\mathbb {R}$
such that, letting
$\mathbb {R}$
such that, letting
![]() $S= \mathbb {R}/\sim $
, there is no good,
$S= \mathbb {R}/\sim $
, there is no good,
![]() $D^\infty _{\text {Lipschitz}}$
-anonymous, weak
$D^\infty _{\text {Lipschitz}}$
-anonymous, weak
![]() $S$
-predictor.
$S$
-predictor.
Our proof of Theorem 19 relies heavily on the proof of [Reference Bajpai and Velleman1, Theorem 8]. Much of the following lemma was implicit in their proof.
Lemma 20 Suppose
![]() $U \subseteq \mathrm{Homeo}^+(\mathbb {R})$
and
$U \subseteq \mathrm{Homeo}^+(\mathbb {R})$
and
![]() $\sim $
is an equivalence relation on
$\sim $
is an equivalence relation on
![]() $\mathbb {R}$
such that:
$\mathbb {R}$
such that:
-
(1) no equivalence class has full measure;Footnote 13 and
-
(2) for every
 $P=(x,y) \in \mathbb {R}^2$
, there exists a
$P=(x,y) \in \mathbb {R}^2$
, there exists a
 $\varphi \in U$
such that:
$\varphi \in U$
such that:-
(a)
 $\varphi (x)=y$
; and
$\varphi (x)=y$
; and -
(b) if
 $z \ne x$
, then
$z \ne x$
, then
 $z \sim \varphi (z)$
; i.e., each equivalence class is closed under
$z \sim \varphi (z)$
; i.e., each equivalence class is closed under
 $\varphi \restriction \left ( \mathbb {R} \setminus \{x \} \right )$
.
$\varphi \restriction \left ( \mathbb {R} \setminus \{x \} \right )$
.
-
Then there is no
![]() $U$
-anonymous, good, weak
$U$
-anonymous, good, weak
![]() $\mathbb {R}/\sim $
-predictor. In fact, the particular function
$\mathbb {R}/\sim $
-predictor. In fact, the particular function
![]() $x \mapsto [x]_\sim $
witnesses the non-goodness of every U-anonymous, weak
$x \mapsto [x]_\sim $
witnesses the non-goodness of every U-anonymous, weak
![]() $\mathbb {R}/\sim $
-predictor.
$\mathbb {R}/\sim $
-predictor.
Proof Let
![]() $S:=\mathbb {R}/\sim $
, and suppose toward a contradiction that
$S:=\mathbb {R}/\sim $
, and suppose toward a contradiction that
![]() $\mathcal {P}:{}^{\mathbb {R}^{\circ }} S \to S$
is a
$\mathcal {P}:{}^{\mathbb {R}^{\circ }} S \to S$
is a
![]() $U$
-anonymous, good, weak
$U$
-anonymous, good, weak
![]() $S$
-predictor. Let
$S$
-predictor. Let
![]() $E: \mathbb {R} \to S$
be defined by
$E: \mathbb {R} \to S$
be defined by
![]() $E(x) = [x]_\sim $
. We will get a contradiction by proving that
$E(x) = [x]_\sim $
. We will get a contradiction by proving that
![]() $\mathcal {P}\Big ( E \setminus \{ x \} \Big ) \ne E(x)$
holds for positively many
$\mathcal {P}\Big ( E \setminus \{ x \} \Big ) \ne E(x)$
holds for positively many
![]() $x$
. It suffices to prove that
$x$
. It suffices to prove that
because if the equivalence class
![]() $C$
were their constant value, then the equation
$C$
were their constant value, then the equation
could hold only if
![]() $x \in C$
; and since
$x \in C$
; and since
![]() $C$
does not have full measure, this would yield positively many
$C$
does not have full measure, this would yield positively many
![]() $x$
where equation (24) fails.
$x$
where equation (24) fails.
To prove (23), pick any
![]() $x,y \in \mathbb {R}$
. By assumption, there is a
$x,y \in \mathbb {R}$
. By assumption, there is a
![]() $\varphi \in U$
such that
$\varphi \in U$
such that
![]() $\varphi (x)=y$
and
$\varphi (x)=y$
and
![]() $z \sim \varphi (z)$
whenever
$z \sim \varphi (z)$
whenever
![]() $z \ne x$
. It follows that
$z \ne x$
. It follows that
![]() $E \setminus \{x \} = E \setminus \{ y \} \circ \varphi \restriction \Big (\mathbb {R} \setminus \{ x \} \Big )$
. Then, by
$E \setminus \{x \} = E \setminus \{ y \} \circ \varphi \restriction \Big (\mathbb {R} \setminus \{ x \} \Big )$
. Then, by
![]() $U$
-anonymity of
$U$
-anonymity of
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $\mathcal {P}\Big ( E \setminus \{ x \} \Big ) = \mathcal {P} \Big ( E \setminus \{ y \} \Big )$
.
$\mathcal {P}\Big ( E \setminus \{ x \} \Big ) = \mathcal {P} \Big ( E \setminus \{ y \} \Big )$
.
Corollary 21 Suppose
![]() $U \subseteq \mathrm{Homeo}^+(\mathbb {R})$
and
$U \subseteq \mathrm{Homeo}^+(\mathbb {R})$
and
![]() $\mathcal {F}$
is a family such that:
$\mathcal {F}$
is a family such that:
-
(1)
 $\mathcal {F}$
is a countable set of partial, injective functions from
$\mathcal {F}$
is a countable set of partial, injective functions from
 $\mathbb {R} \to \mathbb {R}$
;
$\mathbb {R} \to \mathbb {R}$
; -
(2) for every
 $(x,y) \in \mathbb {R}^2$
, there is some
$(x,y) \in \mathbb {R}^2$
, there is some
 $\varphi $
such that:
$\varphi $
such that:-
(a)
 $\varphi \in U$
;
$\varphi \in U$
; -
(b)
 $\varphi (x)=y$
; and
$\varphi (x)=y$
; and -
(c) if
 $z \ne x$
, then there is some
$z \ne x$
, then there is some
 $f \in \mathcal {F}$
such that
$f \in \mathcal {F}$
such that
 $\varphi (z) = f(z)$
.
$\varphi (z) = f(z)$
.
-
Let
![]() $\sim $
be the equivalence relation on
$\sim $
be the equivalence relation on
![]() $\mathbb {R}$
generated by the relation
$\mathbb {R}$
generated by the relation
Then there is no good weak
![]() $U$
-anonymous
$U$
-anonymous
![]() $\mathbb {R}/\sim $
predictor.
$\mathbb {R}/\sim $
predictor.
Proof We verify that
![]() $\sim $
satisfies the assumptions of Lemma 20. Each
$\sim $
satisfies the assumptions of Lemma 20. Each
![]() $\sim $
-equivalence class is countable, because
$\sim $
-equivalence class is countable, because
![]() $\mathcal {F}$
is countable and each member of
$\mathcal {F}$
is countable and each member of
![]() $\mathcal {F}$
is injective (“countable-to-one” would suffice). So each
$\mathcal {F}$
is injective (“countable-to-one” would suffice). So each
![]() $\sim $
-equivalence class not only fails to have full measure, but in fact has measure zero. Consider any
$\sim $
-equivalence class not only fails to have full measure, but in fact has measure zero. Consider any
![]() $(x,y) \in \mathbb {R}^2$
. By assumption, there is a
$(x,y) \in \mathbb {R}^2$
. By assumption, there is a
![]() $\varphi \in U$
such that
$\varphi \in U$
such that
![]() $\varphi (x)=y$
and whenever
$\varphi (x)=y$
and whenever
![]() $z \ne x$
,
$z \ne x$
,
![]() $\varphi (z) = f(z)$
for some
$\varphi (z) = f(z)$
for some
![]() $f \in \mathcal {F}$
. Then
$f \in \mathcal {F}$
. Then
![]() $(z,\varphi (z)) \in R$
and
$(z,\varphi (z)) \in R$
and
![]() $R$
is contained in
$R$
is contained in
![]() $\sim $
, so
$\sim $
, so
![]() $z \sim \varphi (z)$
.
$z \sim \varphi (z)$
.
We first sketch the outline of Bajpai–Velleman’s proof of Theorem 4. They first fix a single, increasing
![]() $C^\infty $
bijection
$C^\infty $
bijection
with vanishing derivatives at the endpoints (i.e.,
![]() $s^{(k)}_-(0) = 0 = s^{(k)}_+(1)$
for all
$s^{(k)}_-(0) = 0 = s^{(k)}_+(1)$
for all
![]() $k \in \mathbb {N}$
, where the minus and the plus denote left and right derivatives, respectively). A rational point is a point in the plane such that both coordinates are rational. By rational line, we will mean a line with positive slope that passes through two distinct rational points.Footnote
14
If
$k \in \mathbb {N}$
, where the minus and the plus denote left and right derivatives, respectively). A rational point is a point in the plane such that both coordinates are rational. By rational line, we will mean a line with positive slope that passes through two distinct rational points.Footnote
14
If
![]() $\Psi :\mathbb {R} \to \mathbb {R}$
is a rational line (i.e., an affine function whose graph is a rational line), we write
$\Psi :\mathbb {R} \to \mathbb {R}$
is a rational line (i.e., an affine function whose graph is a rational line), we write
![]() $s \circ \Psi $
to denote the obvious partial function with domain
$s \circ \Psi $
to denote the obvious partial function with domain
![]() $\Psi ^{-1} \Big ( [0,1] \Big )$
. They show that the countable collection
$\Psi ^{-1} \Big ( [0,1] \Big )$
. They show that the countable collection
witnesses the assumptions of Corollary 21. This basically amounts to showing that, given any
![]() $(x,y) \in \mathbb {R}^2$
, one can form an infinite concatenation of members of
$(x,y) \in \mathbb {R}^2$
, one can form an infinite concatenation of members of
![]() $\mathcal {F}$
to yield a strictly increasing
$\mathcal {F}$
to yield a strictly increasing
![]() $C^\infty $
function
$C^\infty $
function
![]() $h: (-\infty ,x) \to \mathbb {R}$
, whose approach (from the left) to the point
$h: (-\infty ,x) \to \mathbb {R}$
, whose approach (from the left) to the point
![]() $(x,y)$
is flat enough that
$(x,y)$
is flat enough that
![]() $\hat {h}:=h ^\frown (x,y)$
will still be a
$\hat {h}:=h ^\frown (x,y)$
will still be a
![]() $C^\infty $
function from
$C^\infty $
function from
![]() $(-\infty ,x] \to \mathbb {R}$
, with
$(-\infty ,x] \to \mathbb {R}$
, with
![]() $\hat {h}^{(k)}_-(x) = 0$
for all
$\hat {h}^{(k)}_-(x) = 0$
for all
![]() $k \in \mathbb {N}$
. Then extending
$k \in \mathbb {N}$
. Then extending
![]() $\hat {h}$
to all of
$\hat {h}$
to all of
![]() $\mathbb {R}$
(in a
$\mathbb {R}$
(in a
![]() $C^\infty $
manner) is easy.
$C^\infty $
manner) is easy.
We follow a similar strategy to prove Theorem 19, although we must use a different collection in order to avoid vanishing first derivatives. Fix any “bump” function
with the following properties:
-
(i)
 $b(0) = 0 = b(1)$
;
$b(0) = 0 = b(1)$
; -
(ii)
 $b(x)> 0$
for all
$b(x)> 0$
for all
 $x \in (0,1)$
;
$x \in (0,1)$
; -
(iii)
 $b \in C^\infty $
(with one-sided derivatives taken at 0 and 1) and
$b \in C^\infty $
(with one-sided derivatives taken at 0 and 1) and
 $b^{(k)}(0)=0=b^{(k)}(1)$
for all
$b^{(k)}(0)=0=b^{(k)}(1)$
for all
 $k \in \mathbb {N}$
; and
$k \in \mathbb {N}$
; and -
(iv)
 $\int _{[0,1]} b = 1$
.
$\int _{[0,1]} b = 1$
.
To get such a
![]() $b$
, one could start, for example, with the common bump function
$b$
, one could start, for example, with the common bump function
 $$\begin{align*}\Psi(x)= \begin{cases} \exp \left( \frac{-1}{1-x^2}\right), & \text{ if } x \in (-1,1), \\ 0, & \text{ otherwise,} \end{cases} \end{align*}$$
$$\begin{align*}\Psi(x)= \begin{cases} \exp \left( \frac{-1}{1-x^2}\right), & \text{ if } x \in (-1,1), \\ 0, & \text{ otherwise,} \end{cases} \end{align*}$$
let
![]() $\Phi (x)=\Psi (2x-1)$
, and then define
$\Phi (x)=\Psi (2x-1)$
, and then define
![]() $b:[0,1] \to \mathbb {R}$
by
$b:[0,1] \to \mathbb {R}$
by
![]() $b(x) = \frac {\Phi (x)}{\int _{[0,1]} \Phi }$
.
$b(x) = \frac {\Phi (x)}{\int _{[0,1]} \Phi }$
.
Definition 22 Given any point
![]() $A=(p,q)$
, any
$A=(p,q)$
, any
![]() $\Delta>0$
, and any
$\Delta>0$
, and any
![]() $\gamma> 0$
, define
$\gamma> 0$
, define
by
![]() $F_{A,\Delta ,\gamma }$
will serve as a smooth transition function from the point
$F_{A,\Delta ,\gamma }$
will serve as a smooth transition function from the point
![]() $A=(p,q)$
to the point
$A=(p,q)$
to the point
![]() $\big (p+\Delta , q + \Delta (1 + \gamma ) \big )$
, with derivative 1 (and vanishing higher derivatives) at those endpoints (see Figure 2). The
$\big (p+\Delta , q + \Delta (1 + \gamma ) \big )$
, with derivative 1 (and vanishing higher derivatives) at those endpoints (see Figure 2). The
![]() $\Delta $
and
$\Delta $
and
![]() $\gamma $
parameters are used to control the norm of the higher derivatives in our subsequent construction.
$\gamma $
parameters are used to control the norm of the higher derivatives in our subsequent construction.

Figure 2: The function
![]() $F_{A,\Delta ,\gamma }$
.
$F_{A,\Delta ,\gamma }$
.
The key features are:
-
(I)
 $F_{A,\Delta ,\gamma }(p) = q$
and
$F_{A,\Delta ,\gamma }(p) = q$
and
 $F_{A,\Delta ,\gamma }(p+\Delta ) = q + \Delta (1+\gamma )$
;
$F_{A,\Delta ,\gamma }(p+\Delta ) = q + \Delta (1+\gamma )$
; -
(II) The Fundamental Theorem of Calculus and Chain Rule yield, for all
 $x \in [p,p + \Delta ]$
: In particular, since
$x \in [p,p + \Delta ]$
: In particular, since $$\begin{align*}F_{A,\Delta,\gamma}'(x) = \Delta \left( 1 + \gamma b\left( \frac{x-p}{\Delta} \right) \right)\left( \frac{1}{\Delta}\right) =1 + \gamma b\left( \frac{x-p}{\Delta} \right). \end{align*}$$
$$\begin{align*}F_{A,\Delta,\gamma}'(x) = \Delta \left( 1 + \gamma b\left( \frac{x-p}{\Delta} \right) \right)\left( \frac{1}{\Delta}\right) =1 + \gamma b\left( \frac{x-p}{\Delta} \right). \end{align*}$$
 $\gamma> 0$
and
$\gamma> 0$
and
 $b> 0$
on
$b> 0$
on
 $(0,1)$
,
$(0,1)$
,
 $F_{A,\Delta ,\gamma }$
is increasing. Together with (I), it follows that
$F_{A,\Delta ,\gamma }$
is increasing. Together with (I), it follows that
 $F_{A,\Delta ,\gamma }$
is an increasing bijection from
$F_{A,\Delta ,\gamma }$
is an increasing bijection from
 $[p,p+\Delta ]$
to
$[p,p+\Delta ]$
to
 $[q,q+\Delta (1+\gamma )]$
. Moreover, notice that for all
$[q,q+\Delta (1+\gamma )]$
. Moreover, notice that for all
 $x \in [p,p + \Delta ]$
, where
$x \in [p,p + \Delta ]$
, where $$\begin{align*}\lvert F^{\prime}_{A,\Delta,\gamma}(x)-1 \rvert \le \gamma \lVert b \rVert, \end{align*}$$
$$\begin{align*}\lvert F^{\prime}_{A,\Delta,\gamma}(x)-1 \rvert \le \gamma \lVert b \rVert, \end{align*}$$
 $\lVert \cdot \rVert $
denotes the sup-norm.
$\lVert \cdot \rVert $
denotes the sup-norm.
-
(III) Since
 $b(0)=0=b(1)$
,
$b(0)=0=b(1)$
,
 $F_{A,\Delta ,\gamma }'(p) = 1 = F_{A,\Delta ,\gamma }'(p + \Delta )$
.
$F_{A,\Delta ,\gamma }'(p) = 1 = F_{A,\Delta ,\gamma }'(p + \Delta )$
. -
(IV) Following part (II), we see that
so, in particular, $$\begin{align*}\forall k \ge 2 \ \ F^{(k)}_{A,\Delta, \gamma}(x)= \frac{\gamma}{\Delta^{k-1}} b^{(k-1)}\left( \frac{x-p}{\Delta} \right), \end{align*}$$
$$\begin{align*}\forall k \ge 2 \ \ F^{(k)}_{A,\Delta, \gamma}(x)= \frac{\gamma}{\Delta^{k-1}} b^{(k-1)}\left( \frac{x-p}{\Delta} \right), \end{align*}$$
 $$ \begin{align*} \forall k \ge 2 \ \ \lVert F^{(k)}_{A,\Delta,\gamma} \rVert \le \frac{\gamma}{\Delta^{k-1}} \lVert b^{(k-1)} \rVert. \end{align*} $$
$$ \begin{align*} \forall k \ge 2 \ \ \lVert F^{(k)}_{A,\Delta,\gamma} \rVert \le \frac{\gamma}{\Delta^{k-1}} \lVert b^{(k-1)} \rVert. \end{align*} $$
Let
![]() $\mathcal {F}$
denote the collection of all rational lines of positive slope, together with all functions of the form
$\mathcal {F}$
denote the collection of all rational lines of positive slope, together with all functions of the form
![]() $F_{A,\Delta ,\gamma }$
where
$F_{A,\Delta ,\gamma }$
where
![]() $A$
is a rational point and
$A$
is a rational point and
![]() $\Delta $
and
$\Delta $
and
![]() $\gamma $
are positive rational numbers. We will show that
$\gamma $
are positive rational numbers. We will show that
![]() $\mathcal {F}$
satisfies the assumptions of Corollary 21, with
$\mathcal {F}$
satisfies the assumptions of Corollary 21, with
![]() $U:= D^\infty _{\text {Lipschitz}}$
. Clearly,
$U:= D^\infty _{\text {Lipschitz}}$
. Clearly,
![]() $\mathcal {F}$
is countable, and consists of injective functions. It remains to verify clause (2) of Corollary 21.
$\mathcal {F}$
is countable, and consists of injective functions. It remains to verify clause (2) of Corollary 21.
Lemma 23 Given any point
![]() $P=(w,z)$
in the plane, there exist sequences
$P=(w,z)$
in the plane, there exist sequences
![]() $(A_n)_n=(p_n,q_n)_n$
and
$(A_n)_n=(p_n,q_n)_n$
and
![]() $(\gamma _n)_n$
such that:
$(\gamma _n)_n$
such that:
-
(1)
 $(p_n)_n$
and
$(p_n)_n$
and
 $(q_n)_n$
are increasing sequences of rational numbers converging to
$(q_n)_n$
are increasing sequences of rational numbers converging to
 $w$
and
$w$
and
 $z$
, respectively.
$z$
, respectively. -
(2)
 $\gamma _n$
is a positive rational number for all
$\gamma _n$
is a positive rational number for all
 $n$
.
$n$
. -
(3) Let
 $\Delta _n:= p_{n+1}-p_n$
. Then
$\Delta _n:= p_{n+1}-p_n$
. Then
 $0 < \Delta _n < 1$
and
$0 < \Delta _n < 1$
and
 $q_{n+1} = q_n + \Delta _n(1 + \gamma _n)$
for all
$q_{n+1} = q_n + \Delta _n(1 + \gamma _n)$
for all
 $n$
.
$n$
. -
(4)
 $\lim _{n \to \infty } \frac {\gamma _n}{\left (\Delta _n\right )^{n-1}} = 0$
.
$\lim _{n \to \infty } \frac {\gamma _n}{\left (\Delta _n\right )^{n-1}} = 0$
.
Proof Fix an increasing sequence
![]() $(p_n)_n$
of rational numbers converging to
$(p_n)_n$
of rational numbers converging to
![]() $w$
such that
$w$
such that
![]() $\Delta _n := p_{n+1}-p_n < 1$
for all
$\Delta _n := p_{n+1}-p_n < 1$
for all
![]() $n$
. Let
$n$
. Let
![]() $L$
be the line of slope 1 that passes through
$L$
be the line of slope 1 that passes through
![]() $P$
.Footnote
15
For any point
$P$
.Footnote
15
For any point
![]() $B$
, let
$B$
, let
![]() $\text {vDist}(L,B)$
denote the vertical distance from
$\text {vDist}(L,B)$
denote the vertical distance from
![]() $L$
to
$L$
to
![]() $B$
.
$B$
.
Recursively define the
![]() $q_n$
,
$q_n$
,
![]() $A_n$
, and
$A_n$
, and
![]() $\gamma _n$
, together with the auxiliary variable
$\gamma _n$
, together with the auxiliary variable
as follows: fix a rational
![]() $q_1$
such that
$q_1$
such that
![]() $A_1:=(p_1,q_1)$
lies strictly below the line
$A_1:=(p_1,q_1)$
lies strictly below the line
![]() $L$
, and
$L$
, and
Given that
![]() $q_n$
is defined (and hence so are
$q_n$
is defined (and hence so are
![]() $A_n=(p_n,q_n)$
and
$A_n=(p_n,q_n)$
and
![]() $v_n = \text {vDist}(L,A_n)$
), let
$v_n = \text {vDist}(L,A_n)$
), let
![]() $\gamma _n$
be a positive rational number such that
$\gamma _n$
be a positive rational number such that
 $$ \begin{align} v_n - \frac{\left( \Delta_{n+1}\right)^{n+1}}{n+1} < \gamma_n \Delta_n < v_n; \end{align} $$
$$ \begin{align} v_n - \frac{\left( \Delta_{n+1}\right)^{n+1}}{n+1} < \gamma_n \Delta_n < v_n; \end{align} $$
this is possible because the
![]() $\Delta $
’s are positive. Define
$\Delta $
’s are positive. Define
![]() $q_{n+1}:=q_n + \Delta _n(1 + \gamma _n)$
,
$q_{n+1}:=q_n + \Delta _n(1 + \gamma _n)$
,
![]() $A_{n+1} := (p_{n+1},q_{n+1})$
, and
$A_{n+1} := (p_{n+1},q_{n+1})$
, and
![]() $v_{n+1}:= \text {vDist}(L,A_{n+1})$
. Note that
$v_{n+1}:= \text {vDist}(L,A_{n+1})$
. Note that
![]() $q_{n+1}$
is rational, provided that
$q_{n+1}$
is rational, provided that
![]() $q_n$
was rational.
$q_n$
was rational.
We inductively verify that
holds for all
![]() $n$
. It holds for
$n$
. It holds for
![]() $n=1$
by (26). Now, suppose
$n=1$
by (26). Now, suppose
![]() $\text {IH}_n$
holds. Since
$\text {IH}_n$
holds. Since
![]() $L$
has slope 1, it follows from the definition of
$L$
has slope 1, it follows from the definition of
![]() $A_{n+1}$
that
$A_{n+1}$
that
![]() $v_{n+1} = v_n - \gamma _n \Delta _n$
, which by (27) is less than
$v_{n+1} = v_n - \gamma _n \Delta _n$
, which by (27) is less than
![]() $\frac {(\Delta _{n+1})^{n+1}}{n+1}$
; so (IH
$\frac {(\Delta _{n+1})^{n+1}}{n+1}$
; so (IH
![]() $_{n+1}$
) holds.
$_{n+1}$
) holds.
Inequalities (IH
![]() $_n$
) and (27) yield
$_n$
) and (27) yield
and hence
 $$\begin{align*}\frac{\gamma_n}{\left( \Delta_n \right)^{n-1}} < \frac{1}{n} \end{align*}$$
$$\begin{align*}\frac{\gamma_n}{\left( \Delta_n \right)^{n-1}} < \frac{1}{n} \end{align*}$$
for all
![]() $n$
. This ensures part (4) of the lemma.
$n$
. This ensures part (4) of the lemma.
Fix any point
![]() $P=(w,z)$
in the plane, and let
$P=(w,z)$
in the plane, and let
![]() $(A_n)_n=(p_n,q_n)_n$
,
$(A_n)_n=(p_n,q_n)_n$
,
![]() $\Delta _n=p_{n+1}-p_n$
, and
$\Delta _n=p_{n+1}-p_n$
, and
![]() $\gamma _n$
be rational numbers as given by Lemma 23. For each
$\gamma _n$
be rational numbers as given by Lemma 23. For each
![]() $n$
, let
$n$
, let
 $$\begin{align*}F_n:=F_{A_n, \Delta_n, \gamma_n}: [p_n, p_{n+1}] \to [q_n, \underbrace{q_n + \Delta_n(1+\gamma_n)}_{q_{n+1}}] \end{align*}$$
$$\begin{align*}F_n:=F_{A_n, \Delta_n, \gamma_n}: [p_n, p_{n+1}] \to [q_n, \underbrace{q_n + \Delta_n(1+\gamma_n)}_{q_{n+1}}] \end{align*}$$
using notation from Definition 22. See Figure 3.

Figure 3: The
![]() $F_n$
functions.
$F_n$
functions.
Let
![]() $F:= \bigcup _n F_n$
, which maps from
$F:= \bigcup _n F_n$
, which maps from
![]() $[p_1,w) \to \mathbb {R}$
. By (III) on page 19,
$[p_1,w) \to \mathbb {R}$
. By (III) on page 19,
![]() $F_n$
and
$F_n$
and
![]() $F_{n+1}$
meet at the point
$F_{n+1}$
meet at the point
![]() $A_{n+1}$
, both with first derivative 1 and vanishing higher derivatives; in particular,
$A_{n+1}$
, both with first derivative 1 and vanishing higher derivatives; in particular,
By (II), we have the following for all
![]() $n \in \mathbb {N}$
:
$n \in \mathbb {N}$
:
 $$ \begin{align} \forall x \in [p_n,\underbrace{p_n + \Delta_n}_{p_{n+1}} ] \ \lvert F^{\prime}_{n}(x)-1 \rvert \le \gamma_n \lVert b \rVert. \end{align} $$
$$ \begin{align} \forall x \in [p_n,\underbrace{p_n + \Delta_n}_{p_{n+1}} ] \ \lvert F^{\prime}_{n}(x)-1 \rvert \le \gamma_n \lVert b \rVert. \end{align} $$
Since
![]() $\gamma _n \to 0$
as
$\gamma _n \to 0$
as
![]() $n \to \infty $
(by requirements (3) and (4) of Lemma 23), it follows that
$n \to \infty $
(by requirements (3) and (4) of Lemma 23), it follows that
By (IV), the following also holds for all
![]() $n \in \mathbb {N}$
, where
$n \in \mathbb {N}$
, where
![]() $\alpha _{k,n}$
is defined as indicated:
$\alpha _{k,n}$
is defined as indicated:
 $$ \begin{align} \forall k \ge 2 \ \ \lVert F^{(k)}_{n} \rVert \le \underbrace{ \frac{\gamma_n}{(\Delta_n)^{k-1}} }_{\alpha_{k,n}} \lVert b^{(k-1)} \rVert. \end{align} $$
$$ \begin{align} \forall k \ge 2 \ \ \lVert F^{(k)}_{n} \rVert \le \underbrace{ \frac{\gamma_n}{(\Delta_n)^{k-1}} }_{\alpha_{k,n}} \lVert b^{(k-1)} \rVert. \end{align} $$
Requirement (3) of Lemma 23 (that
![]() $0 < \Delta _n < 1$
) ensures that
$0 < \Delta _n < 1$
) ensures that
 $$\begin{align*}n \ge k \ \implies \ 0 < \underbrace{\frac{\gamma_n}{(\Delta_n)^{k-1}}}_{\alpha_{k,n}} \le \frac{\gamma_n}{(\Delta_n)^{n-1}}, \end{align*}$$
$$\begin{align*}n \ge k \ \implies \ 0 < \underbrace{\frac{\gamma_n}{(\Delta_n)^{k-1}}}_{\alpha_{k,n}} \le \frac{\gamma_n}{(\Delta_n)^{n-1}}, \end{align*}$$
the last term of which goes to 0 as
![]() $n \to \infty $
by requirement (4) of Lemma 23. So
$n \to \infty $
by requirement (4) of Lemma 23. So
and together with (31), this yields
This entire construction, starting from Lemma 23, has a straightforward analogue “from the right” of the point
![]() $P=(w,z)$
, yielding a decreasing sequence
$P=(w,z)$
, yielding a decreasing sequence
![]() $(p^R_{n})_n$
of rationals converging to
$(p^R_{n})_n$
of rationals converging to
![]() $w$
, and functions
$w$
, and functions
such that
![]() $F^R_n \in \mathcal {F}$
, and
$F^R_n \in \mathcal {F}$
, and
![]() $F^R:= \bigcup _n F^R_n$
is an increasing
$F^R:= \bigcup _n F^R_n$
is an increasing
![]() $C^\infty $
function from
$C^\infty $
function from
![]() $(w,p_1^R] \to \mathbb {R}$
with nonvanishing first derivative that has the following analogues of the properties above:
$(w,p_1^R] \to \mathbb {R}$
with nonvanishing first derivative that has the following analogues of the properties above:
Let
![]() $\Psi ^L$
be the affine function with slope 1 passing through the rational point
$\Psi ^L$
be the affine function with slope 1 passing through the rational point
![]() $(p_1,q_1)$
,
$(p_1,q_1)$
,
![]() $\Psi ^R$
be the affine function with slope 1 passing through the rational point
$\Psi ^R$
be the affine function with slope 1 passing through the rational point
![]() $(p^R_1, q^R_1)$
, and define
$(p^R_1, q^R_1)$
, and define
![]() $G:\mathbb {R} \to \mathbb {R}$
by
$G:\mathbb {R} \to \mathbb {R}$
by
 $$\begin{align*}G(x)= \begin{cases} \Psi^L(x), & \text{ if } x < p_1, \\ F(x), & \text{ if } x \in [p_1,w), \\ z, & \text{ if } x=w, \\ F^R(x), & \text{ if } x \in (w,p_1^R], \\ \Psi^R(x), & \text{ if } x> p_1^R. \end{cases} \end{align*}$$
$$\begin{align*}G(x)= \begin{cases} \Psi^L(x), & \text{ if } x < p_1, \\ F(x), & \text{ if } x \in [p_1,w), \\ z, & \text{ if } x=w, \\ F^R(x), & \text{ if } x \in (w,p_1^R], \\ \Psi^R(x), & \text{ if } x> p_1^R. \end{cases} \end{align*}$$
Then
![]() $G$
is continuous, invertible, and has the property that for every
$G$
is continuous, invertible, and has the property that for every
![]() $x \ne w$
, there is some
$x \ne w$
, there is some
![]() $f \in \mathcal {F}$
such that
$f \in \mathcal {F}$
such that
![]() $G(x) = f(x)$
.Footnote
16
$G(x) = f(x)$
.Footnote
16
It remains to prove that
![]() $G \in D^\infty _{\text {Lipschitz}}$
. Now,
$G \in D^\infty _{\text {Lipschitz}}$
. Now,
![]() $G$
is affine on
$G$
is affine on
![]() $(-\infty ,p_1]$
and on
$(-\infty ,p_1]$
and on
![]() $[p_1^R,\infty )$
. In particular,
$[p_1^R,\infty )$
. In particular,
So, to prove that
![]() $G \in D^\infty _{\text {Lipschitz}}$
, it suffices to show that
$G \in D^\infty _{\text {Lipschitz}}$
, it suffices to show that
![]() $G \in D^\infty $
; i.e., that both
$G \in D^\infty $
; i.e., that both
![]() $G$
and
$G$
and
![]() $G^{-1}$
are
$G^{-1}$
are
![]() $C^\infty $
functions.Footnote
17
Furthermore, by the Inverse Function Theorem, to prove that the invertible function
$C^\infty $
functions.Footnote
17
Furthermore, by the Inverse Function Theorem, to prove that the invertible function
![]() $G$
is in
$G$
is in
![]() $D^\infty $
, it suffices to show that
$D^\infty $
, it suffices to show that
![]() $G \in C^\infty $
and that
$G \in C^\infty $
and that
![]() $G'$
is never zero. Since
$G'$
is never zero. Since
![]() $F_n$
agrees with
$F_n$
agrees with
![]() $F_{n+1}$
(and
$F_{n+1}$
(and
![]() $F^R_n$
agrees with
$F^R_n$
agrees with
![]() $F^R_{n+1}$
) at all derivatives at their meeting points, and their first derivatives are always positive, the only nontrivial point to deal with is
$F^R_{n+1}$
) at all derivatives at their meeting points, and their first derivatives are always positive, the only nontrivial point to deal with is
![]() $w$
; we will show that:
$w$
; we will show that:
-
•
 $G'(w) = 1$
; and
$G'(w) = 1$
; and -
•
 $G^{(k)}(w) = 0$
, for
$G^{(k)}(w) = 0$
, for
 $k \ge 2$
.
$k \ge 2$
.
We will prove these from the left of
![]() $w$
; the proof from the right is similar. The following lemma is a minor variant [Reference Bajpai and Velleman1, Lemma 7].
$w$
; the proof from the right is similar. The following lemma is a minor variant [Reference Bajpai and Velleman1, Lemma 7].
Lemma 24 Suppose
![]() $f$
is continuous on
$f$
is continuous on
![]() $(a,b]$
, differentiable on
$(a,b]$
, differentiable on
![]() $(a,b)$
, and
$(a,b)$
, and
Then
![]() $f$
is left differentiable at
$f$
is left differentiable at
![]() $b$
, and
$b$
, and
![]() $f^{\prime }_-(b) = L$
.
$f^{\prime }_-(b) = L$
.
Proof Suppose
![]() $(x_n)$
is an arbitrary sequence in
$(x_n)$
is an arbitrary sequence in
![]() $(a,b)$
that converges to
$(a,b)$
that converges to
![]() $b$
. By the Mean Value Theorem, for each
$b$
. By the Mean Value Theorem, for each
![]() $n$
, there is a
$n$
, there is a
![]() $c_n \in (x_n,b)$
such that
$c_n \in (x_n,b)$
such that
![]() $f'(c_n) = \frac {f(b)-f(x_n)}{b-x_n}$
. By assumption,
$f'(c_n) = \frac {f(b)-f(x_n)}{b-x_n}$
. By assumption,
![]() $\lim _{n \to \infty } f'(c_n) = L$
, so
$\lim _{n \to \infty } f'(c_n) = L$
, so
![]() $\lim _{n \to \infty } \frac {f(b)-f(x_n)}{b-x_n} = L$
.
$\lim _{n \to \infty } \frac {f(b)-f(x_n)}{b-x_n} = L$
.
By (28),
![]() $G$
is
$G$
is
![]() $C^\infty $
on
$C^\infty $
on
![]() $(-\infty ,w)$
, and we already noted that
$(-\infty ,w)$
, and we already noted that
![]() $G$
is continuous on
$G$
is continuous on
![]() $\mathbb {R}$
. By (30), continuity of
$\mathbb {R}$
. By (30), continuity of
![]() $G$
, and Lemma 24,
$G$
, and Lemma 24,
![]() $G^{\prime }_-(w) = 1 = \lim _{x \nearrow w} G'(x)$
and hence
$G^{\prime }_-(w) = 1 = \lim _{x \nearrow w} G'(x)$
and hence
![]() $G'$
is continuous on
$G'$
is continuous on
![]() $(-\infty ,w]$
. Then, using (32) (with
$(-\infty ,w]$
. Then, using (32) (with
![]() $k=2$
) and applying Lemma 24 to
$k=2$
) and applying Lemma 24 to
![]() $G'$
, we get that
$G'$
, we get that
![]() $G^{(2)}_-(w) = 0 = \lim _{x \nearrow w} G^{(2)}(x)$
and
$G^{(2)}_-(w) = 0 = \lim _{x \nearrow w} G^{(2)}(x)$
and
![]() $G^{(2)}$
is continuous on
$G^{(2)}$
is continuous on
![]() $(-\infty ,w]$
. Continuing by induction, we get that
$(-\infty ,w]$
. Continuing by induction, we get that
![]() $G^{(k)}_-(w) = 0 = \lim _{x \nearrow w} G^{(k)}(x)$
for all
$G^{(k)}_-(w) = 0 = \lim _{x \nearrow w} G^{(k)}(x)$
for all
![]() $k \ge 2$
.
$k \ge 2$
.
6 Concluding remarks
Hardin–Taylor’s Question 2 (page 2) is still very much open, as there is still a big gap between the “lower frontier” of our Theorem 5 and the “upper frontier” of our Theorem 8.
Our Theorem 5 isolated some (topological) group-theoretic properties that guarantee existence of good anonymous predictors. It is natural to pursue this further. In particular, Theorem 11 implies that any group
![]() $U \le \mathrm{Homeo}^+(I)$
satisfying the assumptions of Theorem 5 is a metabelian group, meaning that its commutator subgroup is abelian. And Theorem 5 encompasses all known examples of groups for which good, anonymous predictors exist (for every set
$U \le \mathrm{Homeo}^+(I)$
satisfying the assumptions of Theorem 5 is a metabelian group, meaning that its commutator subgroup is abelian. And Theorem 5 encompasses all known examples of groups for which good, anonymous predictors exist (for every set
![]() $S$
). This suggests the following question.
$S$
). This suggests the following question.
Question 25 Suppose
![]() $U \le \mathrm{Homeo}^+(\mathbb {R})$
, and for every set
$U \le \mathrm{Homeo}^+(\mathbb {R})$
, and for every set
![]() $S$
, there exists a
$S$
, there exists a
![]() $U$
-anonymous, good
$U$
-anonymous, good
![]() $S$
-predictor. Must
$S$
-predictor. Must
![]() $U$
be metabelian? Must
$U$
be metabelian? Must
![]() $U$
at least be solvable?
$U$
at least be solvable?