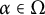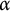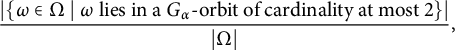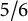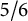1 Introduction
This paper is part of a series [Reference Morris, Moscatiello and Spiga17–Reference Morris, Spiga and Verret19, Reference Spiga24] aiming to obtain an asymptotic enumeration of finite Cayley graphs. However, the main players in this paper are not finite Cayley graphs, but finite transitive groups. Our results on finite transitive groups can then be used to make a considerable step toward the enumeration problem of Cayley graphs and thus getting closer to solving an outstanding question of Babai and Godsil (see [Reference Babai and Godsil2] or [Reference Godsil8, Conjecture 3.13]).
Let G be a finite transitive group on
![]() $\Omega $
, let
$\Omega $
, let
![]() $\alpha \in \Omega $
, and let
$\alpha \in \Omega $
, and let
![]() $G_{\alpha }$
be the stabilizer in G of the point
$G_{\alpha }$
be the stabilizer in G of the point
![]() $\alpha $
. The orbits of
$\alpha $
. The orbits of
![]() $G_{\alpha }$
on
$G_{\alpha }$
on
![]() $\Omega $
are said to be the suborbits of G and their cardinalities are said to be the subdegrees of G. In this paper, we are concerned in finite transitive groups having many subdegrees equal to
$\Omega $
are said to be the suborbits of G and their cardinalities are said to be the subdegrees of G. In this paper, we are concerned in finite transitive groups having many subdegrees equal to
![]() $1$
or
$1$
or
![]() $2$
. In particular, we are interested in the ratio
$2$
. In particular, we are interested in the ratio
 $$ \begin{align*} \mathbf{I}_{\Omega}(G):=\frac{|\{\omega\in \Omega\mid \omega \textrm{ lies in a }G_{\alpha}\textrm{-orbit of cardinality at most 2}\}|}{|\Omega|}. \end{align*} $$
$$ \begin{align*} \mathbf{I}_{\Omega}(G):=\frac{|\{\omega\in \Omega\mid \omega \textrm{ lies in a }G_{\alpha}\textrm{-orbit of cardinality at most 2}\}|}{|\Omega|}. \end{align*} $$
As G is transitive on
![]() $\Omega $
, the value of
$\Omega $
, the value of
![]() $\mathbf {I}_{\Omega }(G)$
does not depend on
$\mathbf {I}_{\Omega }(G)$
does not depend on
![]() $\alpha $
. Clearly,
$\alpha $
. Clearly,
![]() $0<\mathbf {I}_{\Omega }(G)\le 1$
.
$0<\mathbf {I}_{\Omega }(G)\le 1$
.
Theorem 1.1 Let G be a finite transitive group on
![]() $\Omega $
, let
$\Omega $
, let
![]() $\alpha \in \Omega $
, and let
$\alpha \in \Omega $
, and let
![]() $G_{\alpha }$
be the stabilizer in G of the point
$G_{\alpha }$
be the stabilizer in G of the point
![]() $\alpha $
. If
$\alpha $
. If
![]() $\mathbf {I}_{\Omega }(G)>\frac {5}{6},$
then
$\mathbf {I}_{\Omega }(G)>\frac {5}{6},$
then
![]() $\mathbf {I}_G(G_{\alpha })=1$
, that is, each suborbit of G has cardinality at most
$\mathbf {I}_G(G_{\alpha })=1$
, that is, each suborbit of G has cardinality at most
![]() $2$
.
$2$
.
It turns out that finite transitive groups G with
![]() $\mathbf {I}_{\Omega }(G)=1$
are classified by a classical result of Bergman and Lenstra [Reference Bergman and Lenstra3]. The result of Bergman and Lenstra is rather general and applies to arbitrary (i.e., not necessarily finite) groups. The proof of [Reference Bergman and Lenstra3, Theorem 1] is very beautiful and it is based on certain equivalence relations; also the strengthening of Isaacs [Reference Isaacs14] of the theorem of Bergman and Lenstra has a remarkably ingenious proof.
$\mathbf {I}_{\Omega }(G)=1$
are classified by a classical result of Bergman and Lenstra [Reference Bergman and Lenstra3]. The result of Bergman and Lenstra is rather general and applies to arbitrary (i.e., not necessarily finite) groups. The proof of [Reference Bergman and Lenstra3, Theorem 1] is very beautiful and it is based on certain equivalence relations; also the strengthening of Isaacs [Reference Isaacs14] of the theorem of Bergman and Lenstra has a remarkably ingenious proof.
From [Reference Bergman and Lenstra3, Theorem 1], finite transitive groups with
![]() $\mathbf {I}_{\Omega }(G)=1$
can be partitioned in three families:
$\mathbf {I}_{\Omega }(G)=1$
can be partitioned in three families:
-
(a) finite transitive groups G where the stabilizer
 $G_{\alpha }$
has order
$G_{\alpha }$
has order
 $1$
,
$1$
, -
(b) finite transitive groups G where the stabilizer
 $G_{\alpha }$
has order
$G_{\alpha }$
has order
 $2$
,
$2$
, -
(c) finite transitive groups G admitting an elementary abelian normal
 $2$
-subgroup N with
$2$
-subgroup N with
 $|N:G_{\alpha }|=2$
.
$|N:G_{\alpha }|=2$
.
In the first family, each suborbit of G has cardinality
![]() $1$
, that is, G acts regularly on
$1$
, that is, G acts regularly on
![]() $\Omega $
. In the second family, since
$\Omega $
. In the second family, since
![]() $G_{\alpha }$
has cardinality
$G_{\alpha }$
has cardinality
![]() $2$
, each orbit of
$2$
, each orbit of
![]() $G_{\alpha }$
has cardinality at most
$G_{\alpha }$
has cardinality at most
![]() $2$
. In the third family, since
$2$
. In the third family, since
![]() $N\unlhd G$
, the orbits of N on
$N\unlhd G$
, the orbits of N on
![]() $\Omega $
form a system of imprimitivity for the action of G; as
$\Omega $
form a system of imprimitivity for the action of G; as
![]() $|N:G_{\alpha }|=2$
, the blocks of this system of imprimitivity have cardinality
$|N:G_{\alpha }|=2$
, the blocks of this system of imprimitivity have cardinality
![]() $2$
and hence all orbits of
$2$
and hence all orbits of
![]() $G_{\alpha }$
have cardinality at most
$G_{\alpha }$
have cardinality at most
![]() $2$
.
$2$
.
Theorem 1.1 shows that, with respect to the operator
![]() $\mathbf {I}_{\Omega }(G)$
, there is a gap between
$\mathbf {I}_{\Omega }(G)$
, there is a gap between
![]() $5/6$
and
$5/6$
and
![]() $1$
. The value
$1$
. The value
![]() $5/6$
is special: there exist finite transitive groups attaining the value
$5/6$
is special: there exist finite transitive groups attaining the value
![]() $5/6$
.
$5/6$
.
Theorem 1.2 Let G be a finite transitive group on
![]() $\Omega $
, let
$\Omega $
, let
![]() $\alpha \in \Omega $
, and let
$\alpha \in \Omega $
, and let
![]() $G_{\alpha }$
be the stabilizer in G of the point
$G_{\alpha }$
be the stabilizer in G of the point
![]() $\alpha $
. If
$\alpha $
. If
![]() $\mathbf {I}_{\Omega }(G)=\frac {5}{6},$
then there exists an elementary abelian normal
$\mathbf {I}_{\Omega }(G)=\frac {5}{6},$
then there exists an elementary abelian normal
![]() $2$
-subgroup V of G with
$2$
-subgroup V of G with
![]() $|V:G_{\alpha }|=|G_{\alpha }|=4$
.
$|V:G_{\alpha }|=|G_{\alpha }|=4$
.
Moreover, let
![]() $e_1,e_2,e_3,e_4$
be a basis of V, regarded as a four-dimensional vector space over the field with two elements, with
$e_1,e_2,e_3,e_4$
be a basis of V, regarded as a four-dimensional vector space over the field with two elements, with
![]() $G_{\alpha }=\langle e_1,e_2\rangle $
, let
$G_{\alpha }=\langle e_1,e_2\rangle $
, let
![]() $H:=G/\mathbf {C}_G(V)$
where
$H:=G/\mathbf {C}_G(V)$
where
![]() $\mathbf {C}_G(V)$
is the centralizer of V in G, and let K be the stabilizer of the subspace
$\mathbf {C}_G(V)$
is the centralizer of V in G, and let K be the stabilizer of the subspace
![]() $G_{\alpha }$
in
$G_{\alpha }$
in
![]() $\mathrm {GL}(V)$
. Then, H is K-conjugate to one of the following two groups:
$\mathrm {GL}(V)$
. Then, H is K-conjugate to one of the following two groups:
 $$ \begin{align*}\left\langle \begin{pmatrix} 0& 0& 0& 1\\ 1& 1& 0& 0\\ 0& 0& 1& 0\\ 1& 0& 0& 1 \end{pmatrix}, \begin{pmatrix} 1& 1& 1& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1 \end{pmatrix} \right\rangle,\,\,\, \left\langle \begin{pmatrix} 0& 0& 0& 1\\ 1& 1& 0& 0\\ 0& 0& 1& 0\\ 1& 0& 0& 1 \end{pmatrix}, \begin{pmatrix} 1& 1& 1& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1 \end{pmatrix}, \begin{pmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 1& 1& 0& 1\\ 1& 1& 1& 0 \end{pmatrix} \right\rangle. \end{align*} $$
$$ \begin{align*}\left\langle \begin{pmatrix} 0& 0& 0& 1\\ 1& 1& 0& 0\\ 0& 0& 1& 0\\ 1& 0& 0& 1 \end{pmatrix}, \begin{pmatrix} 1& 1& 1& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1 \end{pmatrix} \right\rangle,\,\,\, \left\langle \begin{pmatrix} 0& 0& 0& 1\\ 1& 1& 0& 0\\ 0& 0& 1& 0\\ 1& 0& 0& 1 \end{pmatrix}, \begin{pmatrix} 1& 1& 1& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1 \end{pmatrix}, \begin{pmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 1& 1& 0& 1\\ 1& 1& 1& 0 \end{pmatrix} \right\rangle. \end{align*} $$
The first group has order
![]() $12$
and is isomorphic to the alternating group of degree
$12$
and is isomorphic to the alternating group of degree
![]() $4$
and the second group has order
$4$
and the second group has order
![]() $24$
and is isomorphic to the symmetric group of degree
$24$
and is isomorphic to the symmetric group of degree
![]() $4$
.
$4$
.
Conversely, if G is a finite group containing an elementary abelian normal
![]() $2$
-subgroup
$2$
-subgroup
![]() $V:=\langle e_1,e_2,e_3,e_4\rangle $
of order
$V:=\langle e_1,e_2,e_3,e_4\rangle $
of order
![]() $16$
and
$16$
and
![]() $H:=G/\mathbf {C}_G(V)$
is as above, then the action of G on the set
$H:=G/\mathbf {C}_G(V)$
is as above, then the action of G on the set
![]() $\Omega $
of the right cosets of
$\Omega $
of the right cosets of
![]() $\langle e_1,e_2\rangle $
gives rise to a finite permutation group of degree
$\langle e_1,e_2\rangle $
gives rise to a finite permutation group of degree
![]() $4|G:V|$
with
$4|G:V|$
with
![]() $\mathbf {I}_{\Omega }(G)=5/6$
.
$\mathbf {I}_{\Omega }(G)=5/6$
.
Theorem 1.2 classifies the finite transitive groups attaining the bound
![]() $5/6$
.
$5/6$
.
Before discussing our motivation for proving Theorems 1.1 and 1.2, we make some speculations. A computer search among the transitive groups G of degree at most
![]() $48$
with the computer algebra system magma [Reference Bosma, Cannon and Playoust5] reveals that, if
$48$
with the computer algebra system magma [Reference Bosma, Cannon and Playoust5] reveals that, if
![]() $\mathbf {I}_{\Omega }(G)>1/2$
, then
$\mathbf {I}_{\Omega }(G)>1/2$
, then
![]() $\mathbf { I}_{\Omega }(G)=(q+1)/2q$
, for some
$\mathbf { I}_{\Omega }(G)=(q+1)/2q$
, for some
![]() $q\in \mathbb {Q}$
with
$q\in \mathbb {Q}$
with
![]() $2q\in \mathbb {N}$
. We pose this as a conjecture.
$2q\in \mathbb {N}$
. We pose this as a conjecture.
Conjecture 1.3 Let G be a finite transitive group on
![]() $\Omega $
. If
$\Omega $
. If
![]() $\mathbf {I}_{\Omega }(G)>1/2$
, then
$\mathbf {I}_{\Omega }(G)>1/2$
, then
![]() $\mathbf { I}_{\Omega }(G)=(q+1)/2q$
, for some
$\mathbf { I}_{\Omega }(G)=(q+1)/2q$
, for some
![]() $q\in \mathbb {Q}$
with
$q\in \mathbb {Q}$
with
![]() $2q\in \mathbb {N}$
.
$2q\in \mathbb {N}$
.
If true, Conjecture 1.3 establishes a permutation analog with a classical problem in finite group theory. Let G be a finite group, and let
Miller [Reference Miller16] in 1905 has shown that, if
![]() $\mathbf {I}(G)>3/4$
, then each element of G has order at most
$\mathbf {I}(G)>3/4$
, then each element of G has order at most
![]() $2$
and hence G is an elementary abelian
$2$
and hence G is an elementary abelian
![]() $2$
-group. In this regard, Theorem 1.1 can be seen as a permutation analog of the theorem of Miller, with the only difference that the ratio
$2$
-group. In this regard, Theorem 1.1 can be seen as a permutation analog of the theorem of Miller, with the only difference that the ratio
![]() $3/4$
in the context of abstract groups has to bump up to
$3/4$
in the context of abstract groups has to bump up to
![]() $5/6$
in the context of permutation groups. Miller has also classified the finite groups G with
$5/6$
in the context of permutation groups. Miller has also classified the finite groups G with
![]() $\mathbf {I}(G)=3/4$
. Therefore, Theorem 1.2 can be seen as a permutation analog of the classification of Miller. The theorem of Miller has stimulated a lot of research; for instance, Wall [Reference Wall26] has classified all finite groups G with
$\mathbf {I}(G)=3/4$
. Therefore, Theorem 1.2 can be seen as a permutation analog of the classification of Miller. The theorem of Miller has stimulated a lot of research; for instance, Wall [Reference Wall26] has classified all finite groups G with
![]() $\mathbf {I}(G)>1/2$
. In his proof, Wall uses the Frobenius–Schur formula for counting involutions. An application of this classification shows that, if
$\mathbf {I}(G)>1/2$
. In his proof, Wall uses the Frobenius–Schur formula for counting involutions. An application of this classification shows that, if
![]() $\mathbf {I}(G)>1/2$
, then
$\mathbf {I}(G)>1/2$
, then
![]() $\mathbf {I}(G)=(q+1)/2q$
, for some positive integer q. Therefore, in Conjecture 1.3, we believe that the same type of result holds for the permutation analog
$\mathbf {I}(G)=(q+1)/2q$
, for some positive integer q. Therefore, in Conjecture 1.3, we believe that the same type of result holds for the permutation analog
![]() $\mathbf {I}_{\Omega }(G)$
, but allowing q to be an element of
$\mathbf {I}_{\Omega }(G)$
, but allowing q to be an element of
![]() $\{x/2\mid x\in \mathbb {N}\}$
. As a wishful thinking, we also pose the following problem.
$\{x/2\mid x\in \mathbb {N}\}$
. As a wishful thinking, we also pose the following problem.
Problem 1.4 Classify the finite transitive groups G acting on
![]() $\Omega $
with
$\Omega $
with
![]() $\mathbf {I}_{\Omega }(G)>1/2$
.
$\mathbf {I}_{\Omega }(G)>1/2$
.
Liebeck and MacHale [Reference Liebeck and MacHale15] have generalized the results of Miller and Wall in yet another direction. Indeed, Liebeck and MacHale have classified the finite groups G admitting an automorphism inverting more than half of the elements of G. (The classical results of Miller and Wall can be recovered by considering the identity automorphism.) Then, this classification has been pushed even further by Fitzpatrick [Reference Fitzpatrick7] and Hegarty and MacHale [Reference Hegarty and MacHale10], by classifying the finite groups G admitting an automorphism inverting exactly half of the elements of G. An application of this classification shows that, if
![]() $\alpha $
is an automorphism of G inverting more than half of the elements of G, then the proportion of elements inverted by
$\alpha $
is an automorphism of G inverting more than half of the elements of G, then the proportion of elements inverted by
![]() $\alpha $
is
$\alpha $
is
![]() $(q+1)/2q$
, for some positive integer q. Yet again, another analog with Theorems 1.1 and 1.2, with Conjecture 1.3 and with Problem 1.4. We observe that a partial generalization of this type of results in the context of association schemes is in [Reference Muzychuk and Zieschang20].
$(q+1)/2q$
, for some positive integer q. Yet again, another analog with Theorems 1.1 and 1.2, with Conjecture 1.3 and with Problem 1.4. We observe that a partial generalization of this type of results in the context of association schemes is in [Reference Muzychuk and Zieschang20].
We now discuss our original motivation for proving Theorems 1.1 and 1.2. A digraph
![]() $\Gamma $
is an ordered pair
$\Gamma $
is an ordered pair
![]() $(V,E)$
, where V a finite nonempty set of vertices, and E is a subset of
$(V,E)$
, where V a finite nonempty set of vertices, and E is a subset of
![]() $V\times V$
, representing the arcs. A graph
$V\times V$
, representing the arcs. A graph
![]() $\Gamma $
is a digraph
$\Gamma $
is a digraph
![]() $(V,E)$
, where the binary relation E is symmetric. An automorphism of a (di)graph is a permutation on V that preserves the set E.
$(V,E)$
, where the binary relation E is symmetric. An automorphism of a (di)graph is a permutation on V that preserves the set E.
Definition 1.5 Let R be a group, and let S be a subset of R. The Cayley digraph
![]() $\mathop {\Gamma }(R,S)$
is the digraph with
$\mathop {\Gamma }(R,S)$
is the digraph with
![]() $V=R$
and
$V=R$
and
![]() $(r,t) \in E$
if and only if
$(r,t) \in E$
if and only if
![]() $tr^{-1} \in S$
.
$tr^{-1} \in S$
.
The Cayley digraph is a graph if and only if
![]() $S=S^{-1}$
, that is, S is an inverse-closed subset of R.
$S=S^{-1}$
, that is, S is an inverse-closed subset of R.
The problem of finding graphical regular representations (GRRs) for groups has a long history. Mathematicians have studied graphs with specified automorphism groups at least as far back as the 1930s, and in the 1970s there were many papers devoted to the topic of finding GRRs (see, for example, [Reference Babai1, Reference Hetzel11–Reference Imrich13, Reference Notwitz and Watkins21–Reference Nowitz and Watkins23, Reference Watkins27]), although the “GRR” terminology was coined somewhat later.
Definition 1.6 A digraphical regular representation (DRR) for a group R is a digraph whose full automorphism group is the group R acting regularly on the vertices of the digraph.
Similarly, a GRR for a group R is a graph whose full automorphism group is the group R acting regularly on the vertices of the graph.
It is an easy observation that when
![]() $\mathop {\Gamma }(R,S)$
is a Cayley digraph (graph), the group R acts regularly on the vertices as a group of graph automorphisms. A DRR (or GRR) for R is therefore a Cayley digraph (graph) on R that admits no other automorphisms.
$\mathop {\Gamma }(R,S)$
is a Cayley digraph (graph), the group R acts regularly on the vertices as a group of graph automorphisms. A DRR (or GRR) for R is therefore a Cayley digraph (graph) on R that admits no other automorphisms.
The main thrust of much of the work through the 1970s was to determine which groups admit GRRs. This question was ultimately answered by Godsil in [Reference Godsil9]. The corresponding result for DRRs was proved by a much simpler argument by Babai [Reference Babai1].
Babai and Godsil made the following conjecture. (Given a finite group R,
![]() $2^{\mathbf {c}(R)}$
denotes the number of inverse-closed subsets of R. See Definition 1.10 for the definition of generalized dicyclic group.)
$2^{\mathbf {c}(R)}$
denotes the number of inverse-closed subsets of R. See Definition 1.10 for the definition of generalized dicyclic group.)
Conjecture 1.7 ([Reference Babai and Godsil2]; Conjecture 3.13 [Reference Godsil8])
If R is not generalized dicyclic or abelian of exponent greater than
![]() $2$
, then for almost all inverse-closed subsets S of R,
$2$
, then for almost all inverse-closed subsets S of R,
![]() $\mathop {\Gamma }(R,S)$
is a GRR. In other words,
$\mathop {\Gamma }(R,S)$
is a GRR. In other words,
 $$ \begin{align*}\lim_{|R| \to \infty} \min\left\{ \frac{|\{S \subseteq R: S=S^{-1},\,\mathop{\mathrm{Aut}}(\mathop{\Gamma}(R,S))=R\}|}{2^{\mathbf{c}(R)}}: R\ \mathrm{admits}\ \mathrm{a}\ \mathrm{GRR}\right\} =1.\end{align*} $$
$$ \begin{align*}\lim_{|R| \to \infty} \min\left\{ \frac{|\{S \subseteq R: S=S^{-1},\,\mathop{\mathrm{Aut}}(\mathop{\Gamma}(R,S))=R\}|}{2^{\mathbf{c}(R)}}: R\ \mathrm{admits}\ \mathrm{a}\ \mathrm{GRR}\right\} =1.\end{align*} $$
From Godsil’s theorem [Reference Godsil9], as
![]() $|R|\to \infty $
, the condition “R admits a GRR” is equivalent to “R is neither a generalized dicyclic group, nor abelian of exponent greater than
$|R|\to \infty $
, the condition “R admits a GRR” is equivalent to “R is neither a generalized dicyclic group, nor abelian of exponent greater than
![]() $2$
.”
$2$
.”
The corresponding conjecture for Cayley digraphs (which does not require any families of groups to be excluded) was proved by Morris and the author in [Reference Morris and Spiga18]. Our current strategy for proving the conjecture of Babai and Godsil is to use the proof of the corresponding conjecture for Cayley digraphs as a template and extend the work in [Reference Morris and Spiga18] in the context of undirected Cayley graphs. This strategy so far has been rather successful and in [Reference Morris, Moscatiello and Spiga17, Reference Spiga24] the authors have already adapted some of the arguments in [Reference Morris and Spiga18] for undirected graphs.
One key tool in [Reference Morris and Spiga18] is an elementary observation of Babai.
Lemma 1.8 Let G be a finite transitive group acting on a set
![]() $\Omega $
and properly containing a regular subgroup R. Then there are at most
$\Omega $
and properly containing a regular subgroup R. Then there are at most
![]() $2^{\frac {3|\Omega |}{4}}=2^{\frac {3|R|}{4}}$
Cayley digraphs
$2^{\frac {3|\Omega |}{4}}=2^{\frac {3|R|}{4}}$
Cayley digraphs
![]() $\Gamma $
on R with
$\Gamma $
on R with
![]() $G\leq \mathop {\mathrm {Aut}}(\Gamma )$
.
$G\leq \mathop {\mathrm {Aut}}(\Gamma )$
.
The proof of this fact is elementary (see, for instance, [Reference Morris and Spiga18, Lemma 3.1]). Observe that the number of Cayley digraphs on R is the number of subsets of R, that is,
![]() $2^{|R|}$
. Therefore, Lemma 1.8 says that, given G properly containing R, only at most
$2^{|R|}$
. Therefore, Lemma 1.8 says that, given G properly containing R, only at most
![]() $2^{|R|-\frac {|R|}{4}}$
of these Cayley digraphs admit G as a group of automorphisms. This gain of
$2^{|R|-\frac {|R|}{4}}$
of these Cayley digraphs admit G as a group of automorphisms. This gain of
![]() $|R|/4$
is one of the tools in [Reference Morris and Spiga18] for proving the Babai–Godsil conjecture on Cayley digraphs.
$|R|/4$
is one of the tools in [Reference Morris and Spiga18] for proving the Babai–Godsil conjecture on Cayley digraphs.
To continue our project of proving the Babai–Godsil conjecture for Cayley graphs, we need an analog of Lemma 1.8 for Cayley graphs. Observe that the number of Cayley graphs on R is the number of inverse-closed subsets of R. We denote this number with
![]() $2^{\mathbf {c}(R)}$
. It is not hard to prove (see, for instance, [Reference Morris, Moscatiello and Spiga17, Lemma
$2^{\mathbf {c}(R)}$
. It is not hard to prove (see, for instance, [Reference Morris, Moscatiello and Spiga17, Lemma
![]() $1.12$
]) that
$1.12$
]) that
where
![]() $\mathbf {I}(R)=\{x\in R\mid x^2=1\}$
. To obtain this analog, one needs to investigate finite transitive groups having many suborbits of cardinality at most
$\mathbf {I}(R)=\{x\in R\mid x^2=1\}$
. To obtain this analog, one needs to investigate finite transitive groups having many suborbits of cardinality at most
![]() $2$
. Therefore, our investigation leads to the following result.
$2$
. Therefore, our investigation leads to the following result.
Theorem 1.9 Let G be a finite transitive group properly containing a regular subgroup R. Then one of the following holds:
-
(a) The number of Cayley graphs
 $\Gamma $
on R with
$\Gamma $
on R with
 $G\leq \mathop {\mathrm {Aut}}(\Gamma )$
is at most
$G\leq \mathop {\mathrm {Aut}}(\Gamma )$
is at most
 $2^{\mathbf {c}(R)-\frac {|R|}{96}}$
.
$2^{\mathbf {c}(R)-\frac {|R|}{96}}$
. -
(b) R is abelian of exponent greater than
 $2$
.
$2$
. -
(c) R is generalized dicyclic (see Definition 1.10).
1.1 Notation
In this section, we establish some notation that we use throughout the rest of the paper.
Given a subset X of permutations from
![]() $\Omega $
, we use an exponential notation for the action on
$\Omega $
, we use an exponential notation for the action on
![]() $\Omega $
and hence, in particular, given
$\Omega $
and hence, in particular, given
![]() $\omega \in \Omega $
, we let
$\omega \in \Omega $
, we let
where
![]() $\omega ^x$
is the image of
$\omega ^x$
is the image of
![]() $\omega $
under the permutation x. Similarly, we let
$\omega $
under the permutation x. Similarly, we let
Let G be a transitive permutation group on
![]() $\Omega $
. Recall that a nonempty subset
$\Omega $
. Recall that a nonempty subset
![]() $\Delta $
of
$\Delta $
of
![]() $\Omega $
is said to be a block of imprimitivity if, for every
$\Omega $
is said to be a block of imprimitivity if, for every
![]() $g\in G$
, either
$g\in G$
, either
![]() $\Delta ^g=\Delta $
or
$\Delta ^g=\Delta $
or
![]() $\Delta ^g\cap \Delta =\emptyset $
. Observe that, when
$\Delta ^g\cap \Delta =\emptyset $
. Observe that, when
![]() $\Delta $
is a block of imprimitivity,
$\Delta $
is a block of imprimitivity,
![]() $\{\Delta ^g\mid g\in G\}$
is a partition of the set
$\{\Delta ^g\mid g\in G\}$
is a partition of the set
![]() $\Omega $
and hence
$\Omega $
and hence
![]() $|\Delta |$
divides
$|\Delta |$
divides
![]() $|\Omega |$
.
$|\Omega |$
.
For each positive integer i and for each
![]() $\omega \in \Omega $
, we let
$\omega \in \Omega $
, we let
Observe that,
![]() $\delta \in \Omega _{\omega ,i}$
if and only if
$\delta \in \Omega _{\omega ,i}$
if and only if
![]() $i=|\delta ^{G_{\omega }}|=|G_{\omega }:G_{\omega }\cap G_{\delta }|$
. In particular, since G is transitive on
$i=|\delta ^{G_{\omega }}|=|G_{\omega }:G_{\omega }\cap G_{\delta }|$
. In particular, since G is transitive on
![]() $\Omega $
, we have
$\Omega $
, we have
![]() $|G_{\omega }|=|G_{\delta }|$
and hence
$|G_{\omega }|=|G_{\delta }|$
and hence
![]() $|\delta ^{G_{\omega }}|=|G_{\omega }:G_{\omega }\cap G_{\delta }|=|G_{\delta }:G_{\omega }\cap G_{\delta }|=|\omega ^{G_{\delta }}|$
. Therefore,
$|\delta ^{G_{\omega }}|=|G_{\omega }:G_{\omega }\cap G_{\delta }|=|G_{\delta }:G_{\omega }\cap G_{\delta }|=|\omega ^{G_{\delta }}|$
. Therefore,
We use often (2) in what follows.
Clearly,
and the nonempty sets in this union form a partition of
![]() $\Omega $
.
$\Omega $
.
When
![]() $i:=1$
, we have
$i:=1$
, we have
that is,
![]() $\Omega _{\omega ,1}$
is the set of fixed points of
$\Omega _{\omega ,1}$
is the set of fixed points of
![]() $G_{\omega }$
on
$G_{\omega }$
on
![]() $\Omega $
. It is well known that
$\Omega $
. It is well known that
![]() $\Omega _{\omega ,1}$
is a block of imprimitivity for the action of G on
$\Omega _{\omega ,1}$
is a block of imprimitivity for the action of G on
![]() $\Omega $
(see, for instance, [Reference Dixon and Mortimer6, 1.6.5]). Since this fact will play a role in what follows, we prove it here; this will also be helpful for setting up some additional notation. Let
$\Omega $
(see, for instance, [Reference Dixon and Mortimer6, 1.6.5]). Since this fact will play a role in what follows, we prove it here; this will also be helpful for setting up some additional notation. Let
![]() $\mathbf {N}_{G}(G_{\omega })$
be the normalizer of
$\mathbf {N}_{G}(G_{\omega })$
be the normalizer of
![]() $G_{\omega }$
in G. As
$G_{\omega }$
in G. As
![]() $\mathbf {N}_G(G_{\omega })$
contains
$\mathbf {N}_G(G_{\omega })$
contains
![]() $G_{\omega }$
, the
$G_{\omega }$
, the
![]() $\mathbf { N}_G(G_{\omega })$
-orbit containing
$\mathbf { N}_G(G_{\omega })$
-orbit containing
![]() $\omega $
is a block of imprimitivity for the action of G on
$\omega $
is a block of imprimitivity for the action of G on
![]() $\Omega $
. Therefore, it suffices to prove that
$\Omega $
. Therefore, it suffices to prove that
![]() $\Omega _{\omega ,1}$
is the
$\Omega _{\omega ,1}$
is the
![]() $\mathbf {N}_G(G_{\omega })$
-orbit containing
$\mathbf {N}_G(G_{\omega })$
-orbit containing
![]() $\omega $
, that is,
$\omega $
, that is,
![]() $\Omega _{\omega ,1}=\omega ^{\mathbf {N}_G(G_{\omega })}=\{\omega ^g\mid g\in \mathbf {N}_G(G_{\omega })\}$
. If
$\Omega _{\omega ,1}=\omega ^{\mathbf {N}_G(G_{\omega })}=\{\omega ^g\mid g\in \mathbf {N}_G(G_{\omega })\}$
. If
![]() $g\in \mathbf { N}_G(G_{\omega })$
, then
$g\in \mathbf { N}_G(G_{\omega })$
, then
![]() $G_{\omega }=G_{\omega }^g=G_{\omega ^g}$
and hence
$G_{\omega }=G_{\omega }^g=G_{\omega ^g}$
and hence
![]() $G_{\omega }$
fixes
$G_{\omega }$
fixes
![]() $\omega ^g$
, that is,
$\omega ^g$
, that is,
![]() $\omega ^g\in \Omega _{\omega ,1}$
. Conversely, let
$\omega ^g\in \Omega _{\omega ,1}$
. Conversely, let
![]() $\alpha \in \Omega _{\omega ,1}$
. As G is transitive on
$\alpha \in \Omega _{\omega ,1}$
. As G is transitive on
![]() $\Omega $
, there exists
$\Omega $
, there exists
![]() $g\in G$
with
$g\in G$
with
![]() $\alpha =\omega ^g$
. Thus
$\alpha =\omega ^g$
. Thus
![]() $\omega ^g\in \Omega _{\omega ,1}$
and
$\omega ^g\in \Omega _{\omega ,1}$
and
![]() $G_{\omega }$
fixes
$G_{\omega }$
fixes
![]() $\omega ^g$
. This yields
$\omega ^g$
. This yields
![]() $G_{\omega }=G_{\omega ^g}=G_{\omega }^g$
and
$G_{\omega }=G_{\omega ^g}=G_{\omega }^g$
and
![]() $g\in \mathbf {N}_G(G_{\omega })$
. Therefore,
$g\in \mathbf {N}_G(G_{\omega })$
. Therefore,
![]() $\alpha =\omega ^g$
lies in the
$\alpha =\omega ^g$
lies in the
![]() $\mathbf {N}_G(G_{\omega })$
-orbit containing
$\mathbf {N}_G(G_{\omega })$
-orbit containing
![]() $\omega $
.
$\omega $
.
We let
As G is transitive on
![]() $\Omega $
, d does not depend on
$\Omega $
, d does not depend on
![]() $\omega $
. We claim that, if
$\omega $
. We claim that, if
![]() $g\in G$
and
$g\in G$
and
![]() $\Omega _{\omega ,1}^g\cap \Omega _{\omega ,i}\ne \emptyset $
, then
$\Omega _{\omega ,1}^g\cap \Omega _{\omega ,i}\ne \emptyset $
, then
![]() $\Omega _{\omega ,1}^g\subseteq \Omega _{\omega ,i}$
. To this end, let
$\Omega _{\omega ,1}^g\subseteq \Omega _{\omega ,i}$
. To this end, let
![]() $\alpha \in \Omega _{\omega ,1}^g\cap \Omega _{\omega ,i}$
. As
$\alpha \in \Omega _{\omega ,1}^g\cap \Omega _{\omega ,i}$
. As
![]() $\alpha \in \Omega _{\omega ,1}^g=\Omega _{\omega ^g,1}$
, we deduce that
$\alpha \in \Omega _{\omega ,1}^g=\Omega _{\omega ^g,1}$
, we deduce that
![]() $G_{\omega ^g}$
fixes
$G_{\omega ^g}$
fixes
![]() $\alpha $
and hence
$\alpha $
and hence
![]() $G_{\omega ^g}\le G_{\alpha }$
. Since G is transitive on
$G_{\omega ^g}\le G_{\alpha }$
. Since G is transitive on
![]() $\Omega $
, the subgroups
$\Omega $
, the subgroups
![]() $G_{\omega ^g}$
and
$G_{\omega ^g}$
and
![]() $G_{\alpha }$
have the same cardinality and hence
$G_{\alpha }$
have the same cardinality and hence
![]() $G_{\omega ^g}=G_{\alpha }$
. From this, it follows that
$G_{\omega ^g}=G_{\alpha }$
. From this, it follows that
![]() $\Omega _{\omega ^g,1}=\Omega _{\alpha ,1}$
and hence we need to show that
$\Omega _{\omega ^g,1}=\Omega _{\alpha ,1}$
and hence we need to show that
![]() $\Omega _{\alpha ,1}\subseteq \Omega _{\omega ,i}$
. Let
$\Omega _{\alpha ,1}\subseteq \Omega _{\omega ,i}$
. Let
![]() $\beta \in \Omega _{\alpha ,1}$
; in particular,
$\beta \in \Omega _{\alpha ,1}$
; in particular,
![]() $\Omega _{\alpha ,i}=\Omega _{\beta ,i}$
because
$\Omega _{\alpha ,i}=\Omega _{\beta ,i}$
because
![]() $G_{\alpha }=G_{\beta }$
. As
$G_{\alpha }=G_{\beta }$
. As
![]() $\alpha \in \Omega _{\omega ,i}$
, from (2), we deduce
$\alpha \in \Omega _{\omega ,i}$
, from (2), we deduce
![]() $\omega \in \Omega _{\alpha ,i}=\Omega _{\beta ,i}$
. Another application of (2) gives
$\omega \in \Omega _{\alpha ,i}=\Omega _{\beta ,i}$
. Another application of (2) gives
![]() $\beta \in \Omega _{\omega ,i}$
. Since
$\beta \in \Omega _{\omega ,i}$
. Since
![]() $\beta $
is an arbitrary element of
$\beta $
is an arbitrary element of
![]() $\Omega _{\alpha ,1}$
, we deduce
$\Omega _{\alpha ,1}$
, we deduce
![]() $\Omega _{\alpha ,1}\subseteq \Omega _{\omega ,i}$
.
$\Omega _{\alpha ,1}\subseteq \Omega _{\omega ,i}$
.
Since
![]() $\Omega _{\omega ,1}$
is a block of imprimitivity for the action of G on
$\Omega _{\omega ,1}$
is a block of imprimitivity for the action of G on
![]() $\Omega $
,
$\Omega $
,
![]() $\{\Omega _{\omega ,1}^g\mid g\in G\}$
is a partition of
$\{\Omega _{\omega ,1}^g\mid g\in G\}$
is a partition of
![]() $\Omega $
into subsets of cardinality
$\Omega $
into subsets of cardinality
![]() $|\Omega _{\omega ,1}|=d$
. In particular, from the previous claim, we deduce that d divides
$|\Omega _{\omega ,1}|=d$
. In particular, from the previous claim, we deduce that d divides
![]() $|\Omega _{\omega ,i}|$
, for each positive integer i. We define
$|\Omega _{\omega ,i}|$
, for each positive integer i. We define
 $$ \begin{align} x_i:=\frac{|\Omega_{\omega,i}|}{|\Omega_{\omega,1}|}=\frac{|\Omega_{\omega,i}|}{d}\in\mathbb{N}. \end{align} $$
$$ \begin{align} x_i:=\frac{|\Omega_{\omega,i}|}{|\Omega_{\omega,1}|}=\frac{|\Omega_{\omega,i}|}{d}\in\mathbb{N}. \end{align} $$
In particular,
![]() $x_1:=1$
and, from (3) and (4), we have
$x_1:=1$
and, from (3) and (4), we have
Observe that, as G is transitive on
![]() $\Omega $
,
$\Omega $
,
![]() $|\Omega _{\omega ,i}|$
does not depend on the choice of
$|\Omega _{\omega ,i}|$
does not depend on the choice of
![]() $\omega \in \Omega $
. Thus
$\omega \in \Omega $
. Thus
![]() $x_i$
does not depend on the choice of
$x_i$
does not depend on the choice of
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
Definition 1.10 Let A be an abelian group of even order and of exponent greater than
![]() $2$
, and let y be an involution of A. The generalized dicyclic group
$2$
, and let y be an involution of A. The generalized dicyclic group
![]() $\mathrm {Dic}(A, y, x)$
is the group
$\mathrm {Dic}(A, y, x)$
is the group
![]() $\langle A, x\mid x^2=y, a^x=a^{-1},\forall a\in A\rangle $
. A group is called generalized dicyclic if it is isomorphic to some
$\langle A, x\mid x^2=y, a^x=a^{-1},\forall a\in A\rangle $
. A group is called generalized dicyclic if it is isomorphic to some
![]() $\mathrm {Dic}(A, y, x)$
. When A is cyclic,
$\mathrm {Dic}(A, y, x)$
. When A is cyclic,
![]() $\mathrm {Dic}(A, y, x)$
is called a dicyclic or generalized quaternion group.
$\mathrm {Dic}(A, y, x)$
is called a dicyclic or generalized quaternion group.
2 Lemmata
In this section, we use the notation established in Section 1.1.
Lemma 2.1 Let G be a finite transitive permutation group on a set
![]() $\Omega $
, and let
$\Omega $
, and let
![]() $\alpha \in \Omega $
. If
$\alpha \in \Omega $
. If
then:
-
(a)
 $\Omega =\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
(in particular,
$\Omega =\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
(in particular,
 $\Omega _{\alpha ,i}=\emptyset $
, for every positive integer i with
$\Omega _{\alpha ,i}=\emptyset $
, for every positive integer i with
 $i\notin \{1,2,4\}$
).
$i\notin \{1,2,4\}$
). -
(b) For every
 $\beta \in \Omega _{\alpha ,4}$
,
$\beta \in \Omega _{\alpha ,4}$
,
 $\Omega _{\alpha ,2}\cap \Omega _{\beta ,2}\ne \emptyset $
.
$\Omega _{\alpha ,2}\cap \Omega _{\beta ,2}\ne \emptyset $
. -
(c) For every
 $\beta \in \Omega _{\alpha ,4}$
and for every
$\beta \in \Omega _{\alpha ,4}$
and for every
 $\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}$
, we have
$\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}$
, we have
 $G_{\omega }=(G_{\alpha }\cap G_{\omega }) (G_{\beta }\cap G_{\omega })$
.
$G_{\omega }=(G_{\alpha }\cap G_{\omega }) (G_{\beta }\cap G_{\omega })$
.
Proof As
![]() $|\Omega _{\alpha ,1}|+|\Omega _{\alpha ,2}|<|\Omega |$
, by (3), we get that
$|\Omega _{\alpha ,1}|+|\Omega _{\alpha ,2}|<|\Omega |$
, by (3), we get that
![]() $\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}$
is strictly contained in
$\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}$
is strictly contained in
![]() $\Omega $
. Therefore, let
$\Omega $
. Therefore, let
![]() $\beta \in \Omega \setminus (\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2})$
.
$\beta \in \Omega \setminus (\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2})$
.
Since
![]() $\beta \notin \Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}$
and since the action of G on
$\beta \notin \Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}$
and since the action of G on
![]() $\Omega $
is transitive, we have
$\Omega $
is transitive, we have
See Figure 1.

Figure 1: Auxiliary picture for the proof of Lemma 2.1.
From this, we deduce
Indeed, if, for instance,
![]() $\omega \in \Omega _{\alpha ,1}\cap \Omega _{\beta ,2}$
, then
$\omega \in \Omega _{\alpha ,1}\cap \Omega _{\beta ,2}$
, then
![]() $|\omega ^{G_{\alpha }}|=1$
and
$|\omega ^{G_{\alpha }}|=1$
and
![]() $|\omega ^{G_{\beta }}|=2$
. Therefore,
$|\omega ^{G_{\beta }}|=2$
. Therefore,
![]() $|G_{\alpha }:G_{\alpha }\cap G_{\omega }|=1$
and
$|G_{\alpha }:G_{\alpha }\cap G_{\omega }|=1$
and
![]() $|G_{\beta }:G_{\beta }\cap G_{\omega }|=2$
. As
$|G_{\beta }:G_{\beta }\cap G_{\omega }|=2$
. As
![]() $|G_{\alpha }:G_{\alpha }\cap G_{\omega }|=1$
, we get
$|G_{\alpha }:G_{\alpha }\cap G_{\omega }|=1$
, we get
![]() $G_{\alpha }=G_{\omega }$
. Now, as
$G_{\alpha }=G_{\omega }$
. Now, as
![]() $|G_{\beta }:G_{\beta }\cap G_{\omega }|=2$
and
$|G_{\beta }:G_{\beta }\cap G_{\omega }|=2$
and
![]() $G_{\alpha }=G_{\omega }$
, we get
$G_{\alpha }=G_{\omega }$
, we get
![]() $2=|G_{\beta }:G_{\beta }\cap G_{\omega }|=|G_{\beta }:G_{\beta }\cap G_{\alpha }|$
, which contradicts (5). Therefore,
$2=|G_{\beta }:G_{\beta }\cap G_{\omega }|=|G_{\beta }:G_{\beta }\cap G_{\alpha }|$
, which contradicts (5). Therefore,
![]() $\Omega _{\alpha ,1}\cap \Omega _{\beta ,2}=\emptyset $
. The proof for all other equalities in (6) is similar.
$\Omega _{\alpha ,1}\cap \Omega _{\beta ,2}=\emptyset $
. The proof for all other equalities in (6) is similar.
From (6), we obtain
Recall that, by hypothesis,
![]() $|\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}|>|\Omega |/2$
. Using this together with (7), we get
$|\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}|>|\Omega |/2$
. Using this together with (7), we get
 $$ \begin{align} |\Omega_{\alpha,2}\cap\Omega_{\beta,2}|&=|(\Omega_{\alpha,1}\cup\Omega_{\alpha,2})\cap (\Omega_{\beta,1}\cup\Omega_{\beta,2})|\\ \nonumber &=|\Omega_{\alpha,1}\cup\Omega_{\alpha,2}|+ |\Omega_{\beta,1}\cup\Omega_{\beta,2}|-|(\Omega_{\alpha,1}\cup\Omega_{\alpha,2})\cup (\Omega_{\beta,1}\cup\Omega_{\beta,2})|\\ \nonumber &\ge |\Omega_{\alpha,1}\cup\Omega_{\alpha,2}|+ |\Omega_{\beta,1}\cup\Omega_{\beta,2}|-|\Omega|\\ \nonumber &>\frac{|\Omega|}{2}+\frac{|\Omega|}{2}-|\Omega|=0. \end{align} $$
$$ \begin{align} |\Omega_{\alpha,2}\cap\Omega_{\beta,2}|&=|(\Omega_{\alpha,1}\cup\Omega_{\alpha,2})\cap (\Omega_{\beta,1}\cup\Omega_{\beta,2})|\\ \nonumber &=|\Omega_{\alpha,1}\cup\Omega_{\alpha,2}|+ |\Omega_{\beta,1}\cup\Omega_{\beta,2}|-|(\Omega_{\alpha,1}\cup\Omega_{\alpha,2})\cup (\Omega_{\beta,1}\cup\Omega_{\beta,2})|\\ \nonumber &\ge |\Omega_{\alpha,1}\cup\Omega_{\alpha,2}|+ |\Omega_{\beta,1}\cup\Omega_{\beta,2}|-|\Omega|\\ \nonumber &>\frac{|\Omega|}{2}+\frac{|\Omega|}{2}-|\Omega|=0. \end{align} $$
From (8), we deduce
![]() $\Omega _{\alpha ,2}\cap \Omega _{\beta ,2}\ne \emptyset $
. Let
$\Omega _{\alpha ,2}\cap \Omega _{\beta ,2}\ne \emptyset $
. Let
![]() $\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}$
. In particular,
$\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}$
. In particular,
![]() $|\omega ^{G_{\alpha }}|=|\omega ^{G_{\beta }}|=2$
. This means that
$|\omega ^{G_{\alpha }}|=|\omega ^{G_{\beta }}|=2$
. This means that
![]() $|G_{\alpha }:G_{\alpha }\cap G_{\omega }|=|G_{\beta }:G_{\beta }\cap G_{\omega }|=2$
. Since
$|G_{\alpha }:G_{\alpha }\cap G_{\omega }|=|G_{\beta }:G_{\beta }\cap G_{\omega }|=2$
. Since
![]() $|G_{\alpha }|=|G_{\beta }|=|G_{\omega }|$
, we get that
$|G_{\alpha }|=|G_{\beta }|=|G_{\omega }|$
, we get that
![]() $G_{\alpha }\cap G_{\omega }$
and
$G_{\alpha }\cap G_{\omega }$
and
![]() $G_{\beta }\cap G_{\omega }$
have both index
$G_{\beta }\cap G_{\omega }$
have both index
![]() $2$
in
$2$
in
![]() $G_{\omega }$
. Suppose
$G_{\omega }$
. Suppose
![]() $G_{\alpha }\cap G_{\omega }=G_{\beta }\cap G_{\omega }$
. Then
$G_{\alpha }\cap G_{\omega }=G_{\beta }\cap G_{\omega }$
. Then
and hence
However, this contradicts (5). Therefore,
![]() $G_{\alpha }\cap G_{\omega }$
and
$G_{\alpha }\cap G_{\omega }$
and
![]() $G_{\beta }\cap G_{\omega }$
are two distinct subgroups of
$G_{\beta }\cap G_{\omega }$
are two distinct subgroups of
![]() $G_{\omega }$
having index
$G_{\omega }$
having index
![]() $2$
. This yields
$2$
. This yields
for each
![]() $\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}$
.
$\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}$
.
From (9) and from the fact that
![]() $|G_{\omega }:G_{\alpha }\cap G_{\omega }|=|G_{\omega }:G_{\beta }\cap G_{\omega }|=2$
, we see that
$|G_{\omega }:G_{\alpha }\cap G_{\omega }|=|G_{\omega }:G_{\beta }\cap G_{\omega }|=2$
, we see that
![]() $(G_{\alpha }\cap G_{\omega })\cap (G_{\beta }\cap G_{\omega })=G_{\alpha }\cap G_{\beta }\cap G_{\omega }$
has index
$(G_{\alpha }\cap G_{\omega })\cap (G_{\beta }\cap G_{\omega })=G_{\alpha }\cap G_{\beta }\cap G_{\omega }$
has index
![]() $4$
in
$4$
in
![]() $G_{\omega }$
. Since
$G_{\omega }$
. Since
![]() $|G_{\omega }|=|G_{\alpha }|=|G_{\beta }|$
, we get that
$|G_{\omega }|=|G_{\alpha }|=|G_{\beta }|$
, we get that
![]() $G_{\alpha }\cap G_{\beta }\cap G_{\omega }$
has also index
$G_{\alpha }\cap G_{\beta }\cap G_{\omega }$
has also index
![]() $4$
in
$4$
in
![]() $G_{\alpha }$
and in
$G_{\alpha }$
and in
![]() $G_{\beta }$
. Since
$G_{\beta }$
. Since
![]() $G_{\alpha }\cap G_{\beta }\cap G_{\omega }\le G_{\alpha }\cap G_{\beta }$
, we get that
$G_{\alpha }\cap G_{\beta }\cap G_{\omega }\le G_{\alpha }\cap G_{\beta }$
, we get that
![]() $|G_{\alpha }:G_{\alpha }\cap G_{\beta }|=|G_{\beta }:G_{\alpha }\cap G_{\beta }|$
divides
$|G_{\alpha }:G_{\alpha }\cap G_{\beta }|=|G_{\beta }:G_{\alpha }\cap G_{\beta }|$
divides
![]() $|G_{\alpha }:G_{\alpha }\cap G_{\beta }\cap G_{\omega }|=4$
. As
$|G_{\alpha }:G_{\alpha }\cap G_{\beta }\cap G_{\omega }|=4$
. As
![]() $|G_{\alpha }:G_{\alpha }\cap G_{\beta }|=|G_{\beta }:G_{\alpha }\cap G_{\beta }|>2$
, we get
$|G_{\alpha }:G_{\alpha }\cap G_{\beta }|=|G_{\beta }:G_{\alpha }\cap G_{\beta }|>2$
, we get
![]() $G_{\alpha }\cap G_{\beta }\cap G_{\omega }= G_{\alpha }\cap G_{\beta }$
and
$G_{\alpha }\cap G_{\beta }\cap G_{\omega }= G_{\alpha }\cap G_{\beta }$
and
We have summarized this paragraph in Figure 2. In other words,
![]() $\beta \in \Omega _{\alpha ,4}$
.
$\beta \in \Omega _{\alpha ,4}$
.

Figure 2: Auxiliary picture for the proof of Lemma 2.1.
Since
![]() $\beta $
is an arbitrary element in
$\beta $
is an arbitrary element in
![]() $\Omega \setminus (\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2})$
, we have proven part (a). Now, as
$\Omega \setminus (\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2})$
, we have proven part (a). Now, as
![]() $\Omega _{\alpha ,4}=\Omega \setminus (\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2})$
, part (b) follows from (8) and part (c) follows from (9).
$\Omega _{\alpha ,4}=\Omega \setminus (\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2})$
, part (b) follows from (8) and part (c) follows from (9).
Lemma 2.2 Let G be a finite transitive permutation group on a set
![]() $\Omega $
, and let
$\Omega $
, and let
![]() $\alpha \in \Omega $
. If
$\alpha \in \Omega $
. If
![]() $\Omega =\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
and
$\Omega =\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
and
![]() $|\Omega _{\alpha ,1}|=|\Omega _{\alpha ,4}|$
, then
$|\Omega _{\alpha ,1}|=|\Omega _{\alpha ,4}|$
, then
![]() $\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4}$
is a block of imprimitivity for G. Moreover, for every
$\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4}$
is a block of imprimitivity for G. Moreover, for every
![]() $\beta \in \Omega _{\alpha ,4}$
, we have
$\beta \in \Omega _{\alpha ,4}$
, we have
![]() $\mathbf {N}_G(G_{\alpha })=\mathbf { N}_G(G_{\beta })$
.
$\mathbf {N}_G(G_{\alpha })=\mathbf { N}_G(G_{\beta })$
.
Proof Let
![]() $\beta \in \Omega _{\alpha ,4}$
. As
$\beta \in \Omega _{\alpha ,4}$
. As
![]() $\Omega _{\beta ,1}\subseteq \Omega _{\alpha ,4}$
and as
$\Omega _{\beta ,1}\subseteq \Omega _{\alpha ,4}$
and as
![]() $\Omega _{\beta ,1}$
and
$\Omega _{\beta ,1}$
and
![]() $\Omega _{\alpha ,4}$
have the same cardinality, we deduce
$\Omega _{\alpha ,4}$
have the same cardinality, we deduce
![]() $\Omega _{\alpha ,4}=\Omega _{\beta ,1}$
. Analogously,
$\Omega _{\alpha ,4}=\Omega _{\beta ,1}$
. Analogously,
![]() $\Omega _{\beta ,4}=\Omega _{\alpha ,1}$
.
$\Omega _{\beta ,4}=\Omega _{\alpha ,1}$
.
Let
![]() $g\in G$
with
$g\in G$
with
![]() $\beta =\alpha ^g$
. Now, we have
$\beta =\alpha ^g$
. Now, we have
Analogously,
![]() $\Omega _{\alpha ,1}^g=\Omega _{\alpha ,4}$
. So,
$\Omega _{\alpha ,1}^g=\Omega _{\alpha ,4}$
. So,
Therefore,
![]() $(\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4})^g=\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4}$
and
$(\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4})^g=\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4}$
and
![]() $g^2$
fixes setwise
$g^2$
fixes setwise
![]() $\Omega _{\alpha ,1}$
and
$\Omega _{\alpha ,1}$
and
![]() $\Omega _{\alpha ,4}$
.
$\Omega _{\alpha ,4}$
.
Since
![]() $\Omega _{\alpha ,1}$
is a block of imprimitivity for G with setwise stabilizer
$\Omega _{\alpha ,1}$
is a block of imprimitivity for G with setwise stabilizer
![]() $\mathbf {N}_G(G_{\alpha })$
, we deduce
$\mathbf {N}_G(G_{\alpha })$
, we deduce
![]() $g^2\in \mathbf {N}_G(G_{\alpha })$
. Set
$g^2\in \mathbf {N}_G(G_{\alpha })$
. Set
![]() $T:=\langle \mathbf {N}_G(G_{\alpha }),g\rangle $
.
$T:=\langle \mathbf {N}_G(G_{\alpha }),g\rangle $
.
Since
![]() $G_{\alpha }$
fixes setwise
$G_{\alpha }$
fixes setwise
![]() $\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4}$
, we deduce that
$\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4}$
, we deduce that
![]() $G_{\alpha }$
fixes setwise also
$G_{\alpha }$
fixes setwise also
![]() ${\Omega _{\alpha ,4}=\Omega _{\beta ,1}}$
. Now, for every
${\Omega _{\alpha ,4}=\Omega _{\beta ,1}}$
. Now, for every
![]() $x\in \mathbf {N}_G(G_{\alpha })$
, we have
$x\in \mathbf {N}_G(G_{\alpha })$
, we have
Thus,
![]() $g^{-1}xg$
fixes setwise
$g^{-1}xg$
fixes setwise
![]() $\Omega _{\alpha ,1}$
and hence
$\Omega _{\alpha ,1}$
and hence
![]() $g^{-1}xg\in \mathbf {N}_G(G_{\alpha })$
. This yields
$g^{-1}xg\in \mathbf {N}_G(G_{\alpha })$
. This yields
As g normalizes
![]() $\mathbf {N}_G(G_{\alpha })$
, we have
$\mathbf {N}_G(G_{\alpha })$
, we have
![]() $T=\mathbf {N}_G(G_{\alpha })\langle g\rangle $
and
$T=\mathbf {N}_G(G_{\alpha })\langle g\rangle $
and
Now, since T is an overgroup of
![]() $G_{\alpha }$
and since
$G_{\alpha }$
and since
![]() $\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4}$
is the T-orbit containing
$\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4}$
is the T-orbit containing
![]() $\alpha $
, we deduce that
$\alpha $
, we deduce that
![]() $\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4}$
is a block of imprimitivity for G.
$\Omega _{\alpha ,1}\cup \Omega _{\alpha ,4}$
is a block of imprimitivity for G.
We now need two rather technical lemmas, at first they seem out of context, but their relevance is pivotal in the proof of Lemma 2.5. We could phrase Lemma 2.3 in a purely group theoretic terminology, but it is easier to state in our opinion using some terminology from graph theory.
Lemma 2.3 Let G be a group, let X be an elementary abelian
![]() $2$
-subgroup of G, and let Y be a G-conjugate of X with
$2$
-subgroup of G, and let Y be a G-conjugate of X with
![]() $Z:=X\cap Y$
having index
$Z:=X\cap Y$
having index
![]() $4$
in X and in Y. Let
$4$
in X and in Y. Let
![]() $\Lambda _X:=\{X_1,X_2,X_3\}$
and
$\Lambda _X:=\{X_1,X_2,X_3\}$
and
![]() $\Lambda _{Y}:=\{Y_1,Y_2,Y_3\}$
be the collection of the proper subgroups of X and Y, respectively, properly containing Z.
$\Lambda _{Y}:=\{Y_1,Y_2,Y_3\}$
be the collection of the proper subgroups of X and Y, respectively, properly containing Z.
Let
![]() $\Gamma $
be the bipartite graph having vertex set
$\Gamma $
be the bipartite graph having vertex set
![]() $\Lambda _X\cup \Lambda _Y$
, where a pair
$\Lambda _X\cup \Lambda _Y$
, where a pair
![]() $\{X_i,Y_j\}$
is declared to be adjacent if
$\{X_i,Y_j\}$
is declared to be adjacent if
![]() $X_iY_j$
is a subgroup of G conjugate to X via an element of G. If
$X_iY_j$
is a subgroup of G conjugate to X via an element of G. If
![]() $\Gamma $
has at least six edges, then X commutes with Y.
$\Gamma $
has at least six edges, then X commutes with Y.
Proof Suppose that
-
(*) there exist two distinct vertices of
 $\Gamma $
having valency at least
$\Gamma $
having valency at least
 $2$
.
$2$
.
By symmetry, without loss of generality, we suppose that these two vertices are in
![]() $\Lambda _X$
. Thus, suppose that
$\Lambda _X$
. Thus, suppose that
![]() $X_i,X_j\in \Lambda _X$
have valency at least
$X_i,X_j\in \Lambda _X$
have valency at least
![]() $2$
in
$2$
in
![]() $\Gamma $
.
$\Gamma $
.
Let
![]() $Y_{i_1}$
and
$Y_{i_1}$
and
![]() $Y_{i_2}$
be two neighbors of
$Y_{i_2}$
be two neighbors of
![]() $X_i$
in
$X_i$
in
![]() $\Gamma $
. Then, by definition,
$\Gamma $
. Then, by definition,
![]() $X_iY_{i_1}$
and
$X_iY_{i_1}$
and
![]() $X_iY_{i_2}$
are both subgroups of G conjugate to X. Therefore,
$X_iY_{i_2}$
are both subgroups of G conjugate to X. Therefore,
![]() $X_iY_{i_1}$
and
$X_iY_{i_1}$
and
![]() $X_iY_{i_2}$
are elementary abelian
$X_iY_{i_2}$
are elementary abelian
![]() $2$
-groups and hence
$2$
-groups and hence
![]() $X_i$
commutes with both
$X_i$
commutes with both
![]() $Y_{i_1}$
and
$Y_{i_1}$
and
![]() $Y_{i_2}$
. Since
$Y_{i_2}$
. Since
![]() $\langle Y_{i_1},Y_{i_2}\rangle =Y$
, we deduce that
$\langle Y_{i_1},Y_{i_2}\rangle =Y$
, we deduce that
![]() $X_i$
commutes with Y.
$X_i$
commutes with Y.
Arguing as in the paragraph above with
![]() $X_i$
replaced by
$X_i$
replaced by
![]() $X_j$
, we deduce that
$X_j$
, we deduce that
![]() $X_j$
commutes with Y. Therefore,
$X_j$
commutes with Y. Therefore,
![]() $X=\langle X_i,X_j\rangle $
commutes with Y.
$X=\langle X_i,X_j\rangle $
commutes with Y.
Now, it is elementary to see that every bipartite graph on six vertices, with parts having cardinality
![]() $3$
and having at least six edges has the property
$3$
and having at least six edges has the property
![]() $(\ast )$
.
$(\ast )$
.
Recall that a graph
![]() $\Gamma $
is said to be vertex-transitive if its automorphism group acts transitively on the vertices of
$\Gamma $
is said to be vertex-transitive if its automorphism group acts transitively on the vertices of
![]() $\Gamma $
. Given a vertex
$\Gamma $
. Given a vertex
![]() $\omega $
of
$\omega $
of
![]() $\Gamma $
, we denote by
$\Gamma $
, we denote by
![]() $\Gamma (\omega )$
the neighborhood of
$\Gamma (\omega )$
the neighborhood of
![]() $\omega $
in
$\omega $
in
![]() $\Gamma $
.
$\Gamma $
.
Lemma 2.4 Let
![]() $\Gamma $
be a finite vertex-transitive graph with all vertices of valency
$\Gamma $
be a finite vertex-transitive graph with all vertices of valency
![]() $2$
, let V be the set of vertices of
$2$
, let V be the set of vertices of
![]() $\Gamma $
, let
$\Gamma $
, let
![]() $\omega _1,\omega _2$
be two adjacent vertices of
$\omega _1,\omega _2$
be two adjacent vertices of
![]() $\Gamma $
, and let W be a subset of V containing
$\Gamma $
, and let W be a subset of V containing
![]() $\omega _1$
and
$\omega _1$
and
![]() $\omega _2$
and with the property that, for any two distinct vertices
$\omega _2$
and with the property that, for any two distinct vertices
![]() $\delta _1,\delta _2$
in W,
$\delta _1,\delta _2$
in W,
![]() $V\setminus (\Gamma (\delta _1)\cup \Gamma (\delta _2))\subseteq W$
. Then either
$V\setminus (\Gamma (\delta _1)\cup \Gamma (\delta _2))\subseteq W$
. Then either
![]() $W=V$
or
$W=V$
or
![]() $|V|\le 6$
.
$|V|\le 6$
.
Proof Since
![]() $\Gamma $
is vertex-transitive of valency
$\Gamma $
is vertex-transitive of valency
![]() $2$
,
$2$
,
![]() $\Gamma $
is a disjoint union of s cycles of the same length
$\Gamma $
is a disjoint union of s cycles of the same length
![]() $\ell $
. If
$\ell $
. If
![]() $\ell \ge 7$
or if
$\ell \ge 7$
or if
![]() $\Gamma $
is disconnected, that is,
$\Gamma $
is disconnected, that is,
![]() $s\ge 2$
, it can be easily checked that
$s\ge 2$
, it can be easily checked that
![]() $W=V$
.
$W=V$
.
Lemma 2.5 Let G be a finite transitive permutation group on a set
![]() $\Omega $
, and let
$\Omega $
, and let
![]() $\alpha \in \Omega $
. If
$\alpha \in \Omega $
. If
then one of the following holds:
-
(a)
 $|\Omega _{\alpha ,1}|+|\Omega _{\alpha ,2}|< 5|\Omega |/6$
, or
$|\Omega _{\alpha ,1}|+|\Omega _{\alpha ,2}|< 5|\Omega |/6$
, or - (b)
-
(i)
 $|\Omega _{\alpha ,4}|\le 2|\Omega _{\alpha ,1}|$
,
$|\Omega _{\alpha ,4}|\le 2|\Omega _{\alpha ,1}|$
, -
(ii)
 $G_{\alpha }$
is an elementary abelian
$G_{\alpha }$
is an elementary abelian
 $2$
-group,
$2$
-group, -
(iii)
 $G_{\alpha }$
commutes with
$G_{\alpha }$
commutes with
 $G_{\beta }$
, for every
$G_{\beta }$
, for every
 $\beta \in \Omega _{\alpha ,4}$
, and
$\beta \in \Omega _{\alpha ,4}$
, and -
(iv)
 $\langle G_{\alpha },G_{\beta }\rangle =G_{\alpha }\times G_{\beta }$
is an elementary abelian normal
$\langle G_{\alpha },G_{\beta }\rangle =G_{\alpha }\times G_{\beta }$
is an elementary abelian normal
 $2$
-subgroup of G of order
$2$
-subgroup of G of order
 $16$
, for every
$16$
, for every
 $\beta \in \Omega _{\alpha ,4}$
.
$\beta \in \Omega _{\alpha ,4}$
.
-
Proof From Lemma 2.1,
![]() $\Omega =\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
. Moreover, for each
$\Omega =\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
. Moreover, for each
![]() $\beta \in \Omega _{\alpha ,4}$
, we have shown that
$\beta \in \Omega _{\alpha ,4}$
, we have shown that
![]() $G_{\alpha }$
contains a proper subgroup (namely,
$G_{\alpha }$
contains a proper subgroup (namely,
![]() $G_{\alpha }\cap G_{\omega }$
, for each
$G_{\alpha }\cap G_{\omega }$
, for each
![]() ${\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}}$
) strictly containing
${\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}}$
) strictly containing
![]() $G_{\alpha }\cap G_{\beta }$
. This implies that the permutation group, P say, induced by
$G_{\alpha }\cap G_{\beta }$
. This implies that the permutation group, P say, induced by
![]() $G_{\alpha }$
in its action on the suborbit
$G_{\alpha }$
in its action on the suborbit
![]() $\beta ^{G_{\alpha }}$
is a
$\beta ^{G_{\alpha }}$
is a
![]() $2$
-group. (Indeed, if
$2$
-group. (Indeed, if
![]() $G_{\alpha }$
induces the alternating group
$G_{\alpha }$
induces the alternating group
![]() $\mathrm {Alt}(4)$
or the symmetric group
$\mathrm {Alt}(4)$
or the symmetric group
![]() $\mathrm {Sym}(4)$
on
$\mathrm {Sym}(4)$
on
![]() $\beta ^{G_{\alpha }}$
, then
$\beta ^{G_{\alpha }}$
, then
![]() $G_{\alpha }$
acts primitively on
$G_{\alpha }$
acts primitively on
![]() $\beta ^{G_{\alpha }}$
and hence
$\beta ^{G_{\alpha }}$
and hence
![]() $G_{\alpha }\cap G_{\beta }$
is maximal in
$G_{\alpha }\cap G_{\beta }$
is maximal in
![]() $G_{\alpha }$
.) Clearly, this
$G_{\alpha }$
.) Clearly, this
![]() $2$
-group P must be either cyclic of order
$2$
-group P must be either cyclic of order
![]() $4$
, or elementary abelian of order
$4$
, or elementary abelian of order
![]() $4$
, or dihedral of order
$4$
, or dihedral of order
![]() $8$
.
$8$
.
We have drawn in Figure 3, the lattice of subgroups of the cyclic group of order
![]() $4$
, the elementary abelian group of order
$4$
, the elementary abelian group of order
![]() $4$
and the dihedral group of order
$4$
and the dihedral group of order
![]() $8$
: the dark colored nodes indicate the lattice of subgroups between the whole group and the stabilizer of a point.
$8$
: the dark colored nodes indicate the lattice of subgroups between the whole group and the stabilizer of a point.

Figure 3: Auxiliary picture for the proof of Lemma 2.5.
Figure 3 shows that, given
![]() $G_{\alpha }$
and
$G_{\alpha }$
and
![]() $G_{\alpha }\cap G_{\beta }$
, we only have one choice for
$G_{\alpha }\cap G_{\beta }$
, we only have one choice for
![]() $G_{\alpha }\cap G_{\omega }$
when P is cyclic of order
$G_{\alpha }\cap G_{\omega }$
when P is cyclic of order
![]() $4$
or dihedral of order
$4$
or dihedral of order
![]() $8$
, whereas, we have at most three choices for
$8$
, whereas, we have at most three choices for
![]() $G_{\alpha }\cap G_{\omega }$
when P is elementary abelian of order
$G_{\alpha }\cap G_{\omega }$
when P is elementary abelian of order
![]() $4$
.
$4$
.
Given
![]() $\beta \in \Omega _{\alpha ,4}$
, let
$\beta \in \Omega _{\alpha ,4}$
, let
Observe that in the set
![]() $\mathcal {S}_{\alpha ,\beta }$
, we are collecting point stabilizers and not elements of
$\mathcal {S}_{\alpha ,\beta }$
, we are collecting point stabilizers and not elements of
![]() $\Omega $
and hence different elements
$\Omega $
and hence different elements
![]() $\omega _1,\omega _2$
of
$\omega _1,\omega _2$
of
![]() $\Omega $
can give rise to the same element of
$\Omega $
can give rise to the same element of
![]() $\mathcal {S}_{\alpha ,\beta }$
when
$\mathcal {S}_{\alpha ,\beta }$
when
![]() $G_{\omega _1}=G_{\omega _2}$
.
$G_{\omega _1}=G_{\omega _2}$
.
We claim that
 $$ \begin{align} |\mathcal{S}_{\alpha,\beta}|\le \begin{cases} 3,&\textrm{when the permutation group induced by } G_{\alpha} \textrm{ on } \beta^{G_{\alpha}} \textrm{ or by } G_{\beta} \textrm{ on } \alpha^{G_{\beta}}\\ &\textrm{ is not an elementary abelian } 2\textrm{-group of order } 4,\\ 9,&\textrm{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} |\mathcal{S}_{\alpha,\beta}|\le \begin{cases} 3,&\textrm{when the permutation group induced by } G_{\alpha} \textrm{ on } \beta^{G_{\alpha}} \textrm{ or by } G_{\beta} \textrm{ on } \alpha^{G_{\beta}}\\ &\textrm{ is not an elementary abelian } 2\textrm{-group of order } 4,\\ 9,&\textrm{otherwise}. \end{cases} \end{align} $$
This claim follows from the paragraphs above and from Figure 3. Indeed, from Lemma 2.1 part (c), for each
![]() $X\in \mathcal {S}_{\alpha ,\beta }$
, there exist a proper subgroup A of
$X\in \mathcal {S}_{\alpha ,\beta }$
, there exist a proper subgroup A of
![]() $G_{\alpha }$
and a proper subgroup B of
$G_{\alpha }$
and a proper subgroup B of
![]() $G_{\beta }$
with
$G_{\beta }$
with
![]() $G_{\alpha }\cap G_{\beta }<A$
,
$G_{\alpha }\cap G_{\beta }<A$
,
![]() $G_{\alpha }\cap G_{\beta }<B$
and
$G_{\alpha }\cap G_{\beta }<B$
and
![]() $X=AB$
. Observe that we have at most three choices for A and at most three choices for B and hence at most nine choices for X. Moreover, as long as the permutation group induced on the corresponding orbit is not elementary abelian, we actually have only one choice for either A or B yielding at most three choices for X.
$X=AB$
. Observe that we have at most three choices for A and at most three choices for B and hence at most nine choices for X. Moreover, as long as the permutation group induced on the corresponding orbit is not elementary abelian, we actually have only one choice for either A or B yielding at most three choices for X.
For each
![]() $X\in \mathcal {S}_{\alpha ,\beta }$
, let
$X\in \mathcal {S}_{\alpha ,\beta }$
, let
![]() $\mathcal {S}_X:=\{\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}\mid G_{\omega }=X\}$
. From Section 1.1 and from the notation therein, we have
$\mathcal {S}_X:=\{\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}\mid G_{\omega }=X\}$
. From Section 1.1 and from the notation therein, we have
![]() $|\mathcal {S}_X|=|\Omega _{\omega ,1}|=d$
. From this and from the definition of
$|\mathcal {S}_X|=|\Omega _{\omega ,1}|=d$
. From this and from the definition of
![]() $\mathcal {S}_{\alpha ,\beta }$
, we obtain
$\mathcal {S}_{\alpha ,\beta }$
, we obtain
 $$ \begin{align} |\Omega_{\alpha,2}\cap\Omega_{\beta,2}|=\left|\bigcup_{X\in\mathcal{S}_{\alpha,\beta}}\mathcal{S}_X\right|= \sum_{X\in\mathcal{S}_{\alpha,\beta}}|\mathcal{S}_X|= |\mathcal{S}_{\alpha,\beta}|d. \end{align} $$
$$ \begin{align} |\Omega_{\alpha,2}\cap\Omega_{\beta,2}|=\left|\bigcup_{X\in\mathcal{S}_{\alpha,\beta}}\mathcal{S}_X\right|= \sum_{X\in\mathcal{S}_{\alpha,\beta}}|\mathcal{S}_X|= |\mathcal{S}_{\alpha,\beta}|d. \end{align} $$
From part (a) of Lemma 2.1, we have
![]() $\Omega =\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
. From this, we immediately get
$\Omega =\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
. From this, we immediately get
![]() $\Omega _{\beta ,2}\subseteq \Omega \setminus \Omega _{\alpha ,1}=\Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
and hence
$\Omega _{\beta ,2}\subseteq \Omega \setminus \Omega _{\alpha ,1}=\Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
and hence
![]() $\Omega _{\alpha ,2}\cup \Omega _{\beta ,2}\subseteq \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
. Therefore,
$\Omega _{\alpha ,2}\cup \Omega _{\beta ,2}\subseteq \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}$
. Therefore,
 $$ \begin{align} |\Omega_{\alpha,2}\cap\Omega_{\beta,2}|&=|\Omega_{\alpha,2}|+|\Omega_{\beta,2}|-|\Omega_{\alpha,2}\cup\Omega_{\beta,2}|\\\nonumber &\ge |\Omega_{\alpha,2}|+|\Omega_{\beta,2}|-|\Omega_{\alpha,2}\cup\Omega_{\alpha,4}|\\\nonumber &= |\Omega_{\alpha,2}|+|\Omega_{\beta,2}|-|\Omega_{\alpha,2}|-|\Omega_{\alpha,4}|\\\nonumber &=|\Omega_{\alpha,2}|-|\Omega_{\alpha,4}|. \end{align} $$
$$ \begin{align} |\Omega_{\alpha,2}\cap\Omega_{\beta,2}|&=|\Omega_{\alpha,2}|+|\Omega_{\beta,2}|-|\Omega_{\alpha,2}\cup\Omega_{\beta,2}|\\\nonumber &\ge |\Omega_{\alpha,2}|+|\Omega_{\beta,2}|-|\Omega_{\alpha,2}\cup\Omega_{\alpha,4}|\\\nonumber &= |\Omega_{\alpha,2}|+|\Omega_{\beta,2}|-|\Omega_{\alpha,2}|-|\Omega_{\alpha,4}|\\\nonumber &=|\Omega_{\alpha,2}|-|\Omega_{\alpha,4}|. \end{align} $$
Now, dividing both sides of (11) and (12) by
![]() $|\Omega _{\alpha ,1}|=d$
, by recalling (4) and by rearranging the terms, we obtain
$|\Omega _{\alpha ,1}|=d$
, by recalling (4) and by rearranging the terms, we obtain
We now suppose that part (a) does not hold and we show that part (bi), (bii), (biii), and (biv) are satisfied. In particular, we work under the assumption that
As
![]() $|\Omega |=d(x_1+x_2+x_4)$
,
$|\Omega |=d(x_1+x_2+x_4)$
,
![]() $|\Omega _{\alpha ,1}|+|\Omega _{\alpha ,2}|=d(x_1+x_2)$
and
$|\Omega _{\alpha ,1}|+|\Omega _{\alpha ,2}|=d(x_1+x_2)$
and
![]() $x_1=1$
, the inequality
$x_1=1$
, the inequality
![]() $|\Omega _{\alpha ,1}|+|\Omega _{\alpha ,2}|\ge 5|\Omega |/6$
gives
$|\Omega _{\alpha ,1}|+|\Omega _{\alpha ,2}|\ge 5|\Omega |/6$
gives
Now, (13) yields
![]() $5x_4\le 1+x_2\le 1+|\mathcal {S}_{\alpha ,\beta }|+x_4$
, that is,
$5x_4\le 1+x_2\le 1+|\mathcal {S}_{\alpha ,\beta }|+x_4$
, that is,
![]() $4x_4\le 1+|\mathcal {S}_{\alpha ,\beta }|$
. From (10), we deduce that
$4x_4\le 1+|\mathcal {S}_{\alpha ,\beta }|$
. From (10), we deduce that
![]() $x_4\le 2$
. This already shows part (bi).
$x_4\le 2$
. This already shows part (bi).
When
![]() $x_4=2$
, we deduce
$x_4=2$
, we deduce
![]() $|\mathcal {S}_{\alpha ,\beta }|\ge 7$
and hence (10) yields that the permutation groups induced by
$|\mathcal {S}_{\alpha ,\beta }|\ge 7$
and hence (10) yields that the permutation groups induced by
![]() $G_{\alpha }$
on
$G_{\alpha }$
on
![]() $\beta ^{G_{\alpha }}$
and by
$\beta ^{G_{\alpha }}$
and by
![]() $G_{\beta }$
on
$G_{\beta }$
on
![]() $\alpha ^{G_{\beta }}$
are both elementary abelian
$\alpha ^{G_{\beta }}$
are both elementary abelian
![]() $2$
-groups of order
$2$
-groups of order
![]() $4$
. Since this argument does not depend upon
$4$
. Since this argument does not depend upon
![]() $\beta \in \Omega _{\alpha ,4}$
, we have shown that
$\beta \in \Omega _{\alpha ,4}$
, we have shown that
![]() $G_{\alpha }$
acts as an elementary abelian group on each of its orbits of cardinality
$G_{\alpha }$
acts as an elementary abelian group on each of its orbits of cardinality
![]() $4$
. Since all other orbits of
$4$
. Since all other orbits of
![]() $G_{\alpha }$
have cardinality
$G_{\alpha }$
have cardinality
![]() $1$
or
$1$
or
![]() $2$
, we deduce that
$2$
, we deduce that
![]() $G_{\alpha }$
acts as an elementary abelian
$G_{\alpha }$
acts as an elementary abelian
![]() $2$
-group on each of its orbits and hence
$2$
-group on each of its orbits and hence
![]() $G_{\alpha }$
is an elementary abelian
$G_{\alpha }$
is an elementary abelian
![]() $2$
-group. This shows part (bii), under the additional assumption that
$2$
-group. This shows part (bii), under the additional assumption that
![]() $x_4=2$
. Moreover, as
$x_4=2$
. Moreover, as
![]() $|\mathcal {S}_{\alpha ,\beta }|\ge 7$
, Lemma 2.3 applied with
$|\mathcal {S}_{\alpha ,\beta }|\ge 7$
, Lemma 2.3 applied with
![]() $X:=G_{\alpha }$
and
$X:=G_{\alpha }$
and
![]() $Y:=G_{\beta }$
gives that
$Y:=G_{\beta }$
gives that
![]() $G_{\alpha }$
and
$G_{\alpha }$
and
![]() $G_{\beta }$
commute with each other. This shows that part (biii) is satisfied. To prove part (biv), we use Lemma 2.4. Let
$G_{\beta }$
commute with each other. This shows that part (biii) is satisfied. To prove part (biv), we use Lemma 2.4. Let
![]() $\Gamma $
be the graph having vertex set V, the set of conjugates of
$\Gamma $
be the graph having vertex set V, the set of conjugates of
![]() $G_{\alpha }$
in G, that is,
$G_{\alpha }$
in G, that is,
Then
![]() $|V|=1+x_2+x_4$
. We declare two vertices
$|V|=1+x_2+x_4$
. We declare two vertices
![]() $G_{\omega _1}$
and
$G_{\omega _1}$
and
![]() $G_{\omega _2}$
of
$G_{\omega _2}$
of
![]() $\Gamma $
adjacent if
$\Gamma $
adjacent if
![]() $G_{\omega _1}\cap G_{\omega _2}$
has index
$G_{\omega _1}\cap G_{\omega _2}$
has index
![]() $4$
in
$4$
in
![]() $G_{\omega _1}$
(and hence also in
$G_{\omega _1}$
(and hence also in
![]() $G_{\omega _2}$
). Clearly, the action of G by conjugation gives rise to a vertex-transitive action of G on
$G_{\omega _2}$
). Clearly, the action of G by conjugation gives rise to a vertex-transitive action of G on
![]() $\Gamma $
. As
$\Gamma $
. As
![]() $x_4=2$
,
$x_4=2$
,
![]() $\Gamma $
has valency
$\Gamma $
has valency
![]() $2$
. Let W be the collection of all vertices
$2$
. Let W be the collection of all vertices
![]() $G_{\omega }$
of
$G_{\omega }$
of
![]() $\Gamma $
with
$\Gamma $
with
![]() $G_{\alpha } \cap G_{\beta }\le G_{\omega }$
. Clearly,
$G_{\alpha } \cap G_{\beta }\le G_{\omega }$
. Clearly,
![]() $G_{\alpha },G_{\beta }\in W$
and, from Lemma 2.1 part (c), for any two distinct vertices
$G_{\alpha },G_{\beta }\in W$
and, from Lemma 2.1 part (c), for any two distinct vertices
![]() $G_{\delta _1}$
and
$G_{\delta _1}$
and
![]() $G_{\delta _2}$
of
$G_{\delta _2}$
of
![]() $\Gamma $
contained in W, we have that
$\Gamma $
contained in W, we have that
From this, Lemma 2.4 gives that either
![]() $W=V$
or
$W=V$
or
![]() $|V|\le 6$
. The second alternative gives
$|V|\le 6$
. The second alternative gives
![]() $x_2=|V|-1-x_4\le 3$
, which contradicts the fact that
$x_2=|V|-1-x_4\le 3$
, which contradicts the fact that
![]() $5x_4\le 1+x_2$
. Therefore,
$5x_4\le 1+x_2$
. Therefore,
![]() $W=V$
and hence
$W=V$
and hence
![]() $G_{\alpha }\cap G_{\beta }\le G_{\omega }$
, for every
$G_{\alpha }\cap G_{\beta }\le G_{\omega }$
, for every
![]() $\omega \in \Omega $
. Thus
$\omega \in \Omega $
. Thus
![]() $G_{\alpha }\cap G_{\beta }=1$
and hence
$G_{\alpha }\cap G_{\beta }=1$
and hence
![]() ${G_{\alpha } G_{\beta }=G_{\alpha }\times G_{\beta }}$
is an elementary abelian
${G_{\alpha } G_{\beta }=G_{\alpha }\times G_{\beta }}$
is an elementary abelian
![]() $2$
-group of order
$2$
-group of order
![]() $16$
. To prove that
$16$
. To prove that
![]() ${G_{\alpha }\times G_{\beta }\unlhd G}$
it suffices to apply again this argument to the collection W of all vertices
${G_{\alpha }\times G_{\beta }\unlhd G}$
it suffices to apply again this argument to the collection W of all vertices
![]() $G_{\omega }$
of
$G_{\omega }$
of
![]() $\Gamma $
with
$\Gamma $
with
![]() $G_{\omega }\le G_{\alpha } \times G_{\beta }$
.
$G_{\omega }\le G_{\alpha } \times G_{\beta }$
.
In particular, in the rest of the proof we work under the assumption
![]() $x_4=1$
.
$x_4=1$
.
When
![]() $x_4=1$
, we may refine some of the inequalities above. Indeed, when
$x_4=1$
, we may refine some of the inequalities above. Indeed, when
![]() $x_4=1$
, we have
$x_4=1$
, we have
![]() $\Omega _{\alpha ,4}=\Omega _{\beta ,1}$
, because both sets have the same cardinality and
$\Omega _{\alpha ,4}=\Omega _{\beta ,1}$
, because both sets have the same cardinality and
![]() $\Omega _{\beta ,1}\subseteq \Omega _{\alpha ,4}$
. From this it follows
$\Omega _{\beta ,1}\subseteq \Omega _{\alpha ,4}$
. From this it follows
![]() $\Omega _{\alpha ,2}=\Omega _{\beta ,2}$
. Therefore, from (11), we get
$\Omega _{\alpha ,2}=\Omega _{\beta ,2}$
. Therefore, from (11), we get
Now, the inequality
![]() $5=5x_4\le 1+x_2$
implies
$5=5x_4\le 1+x_2$
implies
![]() $|\mathcal {S}_{\alpha ,\beta }|=x_2\ge 4$
. Again, we may use (10) to deduce that the permutation groups induced by
$|\mathcal {S}_{\alpha ,\beta }|=x_2\ge 4$
. Again, we may use (10) to deduce that the permutation groups induced by
![]() $G_{\alpha }$
on
$G_{\alpha }$
on
![]() $\beta ^{G_{\alpha }}$
and by
$\beta ^{G_{\alpha }}$
and by
![]() $G_{\beta }$
on
$G_{\beta }$
on
![]() $\alpha ^{G_{\beta }}$
are both elementary abelian
$\alpha ^{G_{\beta }}$
are both elementary abelian
![]() $2$
-groups of order
$2$
-groups of order
![]() $4$
. This, as above, yields that
$4$
. This, as above, yields that
![]() $G_{\alpha }$
is an elementary abelian
$G_{\alpha }$
is an elementary abelian
![]() $2$
-group, that is, part (bii) holds.
$2$
-group, that is, part (bii) holds.
From Lemma 2.1 part (c),
![]() $G_{\alpha }\cap G_{\beta }\le G_{\omega }$
, for every
$G_{\alpha }\cap G_{\beta }\le G_{\omega }$
, for every
![]() $\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}$
. In particular,
$\omega \in \Omega _{\alpha ,2}\cap \Omega _{\beta ,2}$
. In particular,
![]() $G_{\alpha }\cap G_{\beta }$
fixes pointwise
$G_{\alpha }\cap G_{\beta }$
fixes pointwise
![]() $\Omega _{\alpha ,2}\cap \Omega _{\beta ,2}$
. As
$\Omega _{\alpha ,2}\cap \Omega _{\beta ,2}$
. As
![]() $\Omega _{\alpha ,2}\cap \Omega _{\beta ,2}=\Omega _{\alpha ,2}$
, we deduce that
$\Omega _{\alpha ,2}\cap \Omega _{\beta ,2}=\Omega _{\alpha ,2}$
, we deduce that
![]() $G_{\alpha }\cap G_{\beta }$
fixes pointwise
$G_{\alpha }\cap G_{\beta }$
fixes pointwise
![]() $\Omega _{\alpha ,2}$
. Since
$\Omega _{\alpha ,2}$
. Since
![]() $G_{\alpha }\cap G_{\beta }$
fixes pointwise also
$G_{\alpha }\cap G_{\beta }$
fixes pointwise also
![]() $\Omega _{\alpha ,1}$
and
$\Omega _{\alpha ,1}$
and
![]() $\Omega _{\beta ,1}=\Omega _{\alpha ,4}$
, we obtain that
$\Omega _{\beta ,1}=\Omega _{\alpha ,4}$
, we obtain that
![]() $G_{\alpha }\cap G_{\beta }$
fixes pointwise
$G_{\alpha }\cap G_{\beta }$
fixes pointwise
![]() $\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}=\Omega $
. Thus
$\Omega _{\alpha ,1}\cup \Omega _{\alpha ,2}\cup \Omega _{\alpha ,4}=\Omega $
. Thus
![]() $G_{\alpha }\cap G_{\beta }=1$
and
$G_{\alpha }\cap G_{\beta }=1$
and
![]() $|G_{\alpha }|=4$
. Observe also that when
$|G_{\alpha }|=4$
. Observe also that when
![]() $x_4=1$
, the hypothesis of Lemma 2.2 is satisfied and hence
$x_4=1$
, the hypothesis of Lemma 2.2 is satisfied and hence
![]() $\mathbf {N}_G(G_{\alpha })=\mathbf {N}_G(G_{\beta })$
. Therefore,
$\mathbf {N}_G(G_{\alpha })=\mathbf {N}_G(G_{\beta })$
. Therefore,
![]() $G_{\beta }$
normalizes
$G_{\beta }$
normalizes
![]() $G_{\alpha }$
. This gives that the commutator subgroup
$G_{\alpha }$
. This gives that the commutator subgroup
![]() $[G_{\alpha },G_{\beta }]$
lies in
$[G_{\alpha },G_{\beta }]$
lies in
![]() $G_{\alpha }\cap G_{\beta }=1$
, that is,
$G_{\alpha }\cap G_{\beta }=1$
, that is,
![]() $G_{\alpha }$
commutes with
$G_{\alpha }$
commutes with
![]() $G_{\beta }$
. This shows that part (biii) is satisfied. Now, as
$G_{\beta }$
. This shows that part (biii) is satisfied. Now, as
![]() $\Omega _{\alpha ,2}=\Omega _{\beta ,2}$
, Lemma 2.1 part (c) yields
$\Omega _{\alpha ,2}=\Omega _{\beta ,2}$
, Lemma 2.1 part (c) yields
![]() $G_{\omega }\le G_{\alpha }\times G_{\beta }$
, for every
$G_{\omega }\le G_{\alpha }\times G_{\beta }$
, for every
![]() $\omega \in \Omega _{\alpha ,2}$
. Therefore,
$\omega \in \Omega _{\alpha ,2}$
. Therefore,
![]() $G_{\alpha }\times G_{\beta }$
contains
$G_{\alpha }\times G_{\beta }$
contains
![]() $G_{\omega }$
, for every
$G_{\omega }$
, for every
![]() $\omega \in \Omega $
. Thus,
$\omega \in \Omega $
. Thus,
and
![]() $G_{\alpha }\times G_{\beta }$
has order
$G_{\alpha }\times G_{\beta }$
has order
![]() $16$
. Thus, part (biv) is satisfied.
$16$
. Thus, part (biv) is satisfied.
We need one final preliminary lemma, with a somehow different flavor. We denote by
![]() $C_2$
and
$C_2$
and
![]() $C_4$
the cyclic groups of order
$C_4$
the cyclic groups of order
![]() $2$
and
$2$
and
![]() $4$
, respectively, we denote by
$4$
, respectively, we denote by
![]() $Q_8$
the quaternion group of order
$Q_8$
the quaternion group of order
![]() $8$
and we denote by
$8$
and we denote by
![]() $D_8$
the dihedral group of order
$D_8$
the dihedral group of order
![]() $4$
.
$4$
.
Lemma 2.6 Let R be a finite group, let U be a proper subgroup of R, and let
![]() $1\ne r\in U$
be a central involution of R. Let
$1\ne r\in U$
be a central involution of R. Let
![]() $\tau :R\to R$
be the permutation defined by
$\tau :R\to R$
be the permutation defined by
 $$ \begin{align*}x\mapsto x^{\tau}:= \begin{cases} x,&\textrm{when }x\in U,\\ xr,&\textrm{when }x\in R\setminus U. \end{cases} \end{align*} $$
$$ \begin{align*}x\mapsto x^{\tau}:= \begin{cases} x,&\textrm{when }x\in U,\\ xr,&\textrm{when }x\in R\setminus U. \end{cases} \end{align*} $$
Then one of the following holds:
-
(a) The number of inverse-closed subsets S of R with
 $S^{\tau }=S$
is at most
$S^{\tau }=S$
is at most
 $2^{\mathbf { c}(R)-\frac {|R|}{48}}$
.
$2^{\mathbf { c}(R)-\frac {|R|}{48}}$
. -
(b) R is generalized dicyclic.
-
(c)
 $R\cong C_4\times C_2^{\ell }$
, for some nonnegative integer
$R\cong C_4\times C_2^{\ell }$
, for some nonnegative integer
 $\ell $
.
$\ell $
.
Proof Let
![]() $\iota :R\to R$
be the permutation defined by
$\iota :R\to R$
be the permutation defined by
![]() $x^{\iota }=x^{-1}$
, for every
$x^{\iota }=x^{-1}$
, for every
![]() $x\in R$
, and let
$x\in R$
, and let
Observe that
![]() $\iota \tau =\tau \iota $
and
$\iota \tau =\tau \iota $
and
![]() $\iota ^2=\tau ^2=1$
. Therefore, T is an elementary abelian
$\iota ^2=\tau ^2=1$
. Therefore, T is an elementary abelian
![]() $2$
-group of order at most
$2$
-group of order at most
![]() $4$
.
$4$
.
Now, a subset S of R is inverse-closed and
![]() $\tau $
-invariant if and only if S is T-invariant. In particular, the number of inverse-closed subsets S of R with
$\tau $
-invariant if and only if S is T-invariant. In particular, the number of inverse-closed subsets S of R with
![]() $S^{\tau }=S$
is
$S^{\tau }=S$
is
![]() $2^{\kappa }$
, where
$2^{\kappa }$
, where
![]() $\kappa $
is the number of orbits of T on R. To compute
$\kappa $
is the number of orbits of T on R. To compute
![]() $\kappa $
, we use the orbit-counting lemma, which says that
$\kappa $
, we use the orbit-counting lemma, which says that
Observe that
 $$ \begin{align} \mathrm{Fix}_R(1)&:=R,\\\nonumber \mathrm{Fix}_R(\iota)&:=\mathbf{I}(R),\\\nonumber \mathrm{Fix}_R(\tau)&:=U, \\\nonumber \mathrm{Fix}_R(\iota\tau)&:=\mathbf{I}(U)\cup\{x\in R\setminus U\mid x^2=r\}.\nonumber \end{align} $$
$$ \begin{align} \mathrm{Fix}_R(1)&:=R,\\\nonumber \mathrm{Fix}_R(\iota)&:=\mathbf{I}(R),\\\nonumber \mathrm{Fix}_R(\tau)&:=U, \\\nonumber \mathrm{Fix}_R(\iota\tau)&:=\mathbf{I}(U)\cup\{x\in R\setminus U\mid x^2=r\}.\nonumber \end{align} $$
Observe that
![]() $\tau \ne 1$
because U is a proper subgroup of R and
$\tau \ne 1$
because U is a proper subgroup of R and
![]() $r\ne 1$
. If
$r\ne 1$
. If
![]() $\iota =1$
, then R is an elementary abelian
$\iota =1$
, then R is an elementary abelian
![]() $2$
-group and
$2$
-group and
![]() $T=\langle \tau \rangle $
. Thus, (14) and (15) yield
$T=\langle \tau \rangle $
. Thus, (14) and (15) yield
 $$ \begin{align*} \kappa&=\frac{1}{2}\left(|R|+|U|\right)\le\frac{|R|}{2}+\frac{|R|}{4}= \frac{3|R|}{4}\\ &=|R|-\frac{|R|}{4}=\mathbf{c}(R)-\frac{|R|}{4}. \end{align*} $$
$$ \begin{align*} \kappa&=\frac{1}{2}\left(|R|+|U|\right)\le\frac{|R|}{2}+\frac{|R|}{4}= \frac{3|R|}{4}\\ &=|R|-\frac{|R|}{4}=\mathbf{c}(R)-\frac{|R|}{4}. \end{align*} $$
Therefore, part (a) holds and the proof follows in this case. Suppose now
![]() $\iota =\tau $
. This means that U is an elementary abelian
$\iota =\tau $
. This means that U is an elementary abelian
![]() $2$
-subgroup of R and
$2$
-subgroup of R and
![]() $x^{-1}=xr$
, for every
$x^{-1}=xr$
, for every
![]() ${x\in R\setminus U}$
. In other words, all elements in U square to
${x\in R\setminus U}$
. In other words, all elements in U square to
![]() $1$
and all elements in
$1$
and all elements in
![]() $R\setminus U$
square to r. Let
$R\setminus U$
square to r. Let
![]() $\bar {R}:=R/\langle r\rangle $
and let us use the “bar” notation for the subgroups and for the elements of
$\bar {R}:=R/\langle r\rangle $
and let us use the “bar” notation for the subgroups and for the elements of
![]() $\bar {R}$
. Consider the function
$\bar {R}$
. Consider the function
defined by
![]() $( x\langle r\rangle , y\langle r\rangle )=x^{-1}y^{-1}xy$
, for every
$( x\langle r\rangle , y\langle r\rangle )=x^{-1}y^{-1}xy$
, for every
![]() $x,y\in R$
. Similarly, consider the function
$x,y\in R$
. Similarly, consider the function
defined by
![]() $q(x\langle r\rangle )=x^2$
. It is not hard to see that, regarding
$q(x\langle r\rangle )=x^2$
. It is not hard to see that, regarding
![]() $\bar {R}$
as a vector space over the field with two elements,
$\bar {R}$
as a vector space over the field with two elements,
![]() $(\cdot ,\cdot )$
is a bilinear form and q is a quadratic form polarizing to
$(\cdot ,\cdot )$
is a bilinear form and q is a quadratic form polarizing to
![]() $(\cdot ,\cdot )$
, that is,
$(\cdot ,\cdot )$
, that is,
for every
![]() $\bar {x},\bar {y}\in \bar {R}$
. Using this terminology, we have that each element of
$\bar {x},\bar {y}\in \bar {R}$
. Using this terminology, we have that each element of
![]() $\bar {U}$
is totally singular and each element of
$\bar {U}$
is totally singular and each element of
![]() $\bar {R}\setminus \bar {U}$
is nondegenerate. From the classification of the quadratic forms over finite fields, we have
$\bar {R}\setminus \bar {U}$
is nondegenerate. From the classification of the quadratic forms over finite fields, we have
![]() $|\bar {R}:\bar {U}|\in \{2,4\}$
. When
$|\bar {R}:\bar {U}|\in \{2,4\}$
. When
![]() $|\bar {R}:\bar {U}|=2$
, we deduce that R is an abelian group isomorphic to the direct product
$|\bar {R}:\bar {U}|=2$
, we deduce that R is an abelian group isomorphic to the direct product
![]() $C_4\times C_2^{\ell }$
, for some
$C_4\times C_2^{\ell }$
, for some
![]() $\ell \ge 0$
. In particular, part (c) holds. When
$\ell \ge 0$
. In particular, part (c) holds. When
![]() $|\bar {R}:\bar {U}|=4$
, we deduce that
$|\bar {R}:\bar {U}|=4$
, we deduce that
![]() $R\cong Q_8\times C_2^{\ell }$
, for some
$R\cong Q_8\times C_2^{\ell }$
, for some
![]() $\ell \ge 0$
. In particular, R is generalized dicyclic and part (b) holds. For the rest of our argument, we may suppose that
$\ell \ge 0$
. In particular, R is generalized dicyclic and part (b) holds. For the rest of our argument, we may suppose that
![]() $\tau \ne \iota \ne 1$
.
$\tau \ne \iota \ne 1$
.
Set
![]() $\mathcal {S}:=\{x\in R\setminus U\mid x^2=r\}$
. In the present situation,
$\mathcal {S}:=\{x\in R\setminus U\mid x^2=r\}$
. In the present situation,
![]() $T=\langle \iota ,\tau \rangle $
has order
$T=\langle \iota ,\tau \rangle $
has order
![]() $4$
and hence, from (15), (14) becomes
$4$
and hence, from (15), (14) becomes
 $$ \begin{align} \kappa&= \frac{1}{4} \left( |\mathrm{Fix}_R(1)|+ |\mathrm{Fix}_R(\iota)|+ |\mathrm{Fix}_R(\tau)|+ |\mathrm{Fix}_R(\tau\iota)| \right)\\\nonumber &=\frac{1}{4}\left( |R|+|\mathbf{I}(R)|+|U|+|\mathbf{I}(U)|+|\{x\in R\setminus U\mid x^2=r\}|\right)\\\nonumber &\le \frac{1}{4}\left( |R|+|\mathbf{I}(R)|+|U|+|\mathbf{I}(R)|+|\mathcal{S}|\right)\\\nonumber &=\frac{|R|+|\mathbf{I}(R)|}{2}-\left( \frac{|R|}{4}-\frac{|U|}{4}-\frac{|\mathcal{S}|}{4} \right)=\mathbf{c}(R)-\left( \frac{|R|}{4}-\frac{|U|}{4}-\frac{|\mathcal{S}|}{4} \right).\nonumber \end{align} $$
$$ \begin{align} \kappa&= \frac{1}{4} \left( |\mathrm{Fix}_R(1)|+ |\mathrm{Fix}_R(\iota)|+ |\mathrm{Fix}_R(\tau)|+ |\mathrm{Fix}_R(\tau\iota)| \right)\\\nonumber &=\frac{1}{4}\left( |R|+|\mathbf{I}(R)|+|U|+|\mathbf{I}(U)|+|\{x\in R\setminus U\mid x^2=r\}|\right)\\\nonumber &\le \frac{1}{4}\left( |R|+|\mathbf{I}(R)|+|U|+|\mathbf{I}(R)|+|\mathcal{S}|\right)\\\nonumber &=\frac{|R|+|\mathbf{I}(R)|}{2}-\left( \frac{|R|}{4}-\frac{|U|}{4}-\frac{|\mathcal{S}|}{4} \right)=\mathbf{c}(R)-\left( \frac{|R|}{4}-\frac{|U|}{4}-\frac{|\mathcal{S}|}{4} \right).\nonumber \end{align} $$
If
![]() $\mathcal {S}=\emptyset $
, then the proof follows immediately from (16), indeed, part (a) holds true. Therefore, for the rest of the proof, we suppose
$\mathcal {S}=\emptyset $
, then the proof follows immediately from (16), indeed, part (a) holds true. Therefore, for the rest of the proof, we suppose
To conclude, we divide the proof in various cases.
Suppose that
![]() $|R:U|=2$
. Let
$|R:U|=2$
. Let
![]() $x\in \mathcal {S}$
and observe that
$x\in \mathcal {S}$
and observe that
![]() $R=U\cup Ux$
. Now, a computation yields
$R=U\cup Ux$
. Now, a computation yields
When
![]() $\mathcal {S}=Ux$
, the action of x on U by conjugation is an automorphism of U inverting each element of U. Therefore, U is abelian and R is generalized dicyclic. Hence part (b) holds. When
$\mathcal {S}=Ux$
, the action of x on U by conjugation is an automorphism of U inverting each element of U. Therefore, U is abelian and R is generalized dicyclic. Hence part (b) holds. When
![]() $\mathcal {S}\subsetneq Ux$
, the result of Liebeck and MacHale [Reference Liebeck and MacHale15] shows that the automorphism x can invert at most
$\mathcal {S}\subsetneq Ux$
, the result of Liebeck and MacHale [Reference Liebeck and MacHale15] shows that the automorphism x can invert at most
![]() $3/4$
of the elements of U and hence
$3/4$
of the elements of U and hence
![]() $|\mathcal {S}|\le 3|U|/4=3|R|/8$
. Now, (16) gives
$|\mathcal {S}|\le 3|U|/4=3|R|/8$
. Now, (16) gives
![]() $\kappa \le \mathbf {c}(R)-|R|/32$
; hence, part (a) holds and the proof in this case follows.
$\kappa \le \mathbf {c}(R)-|R|/32$
; hence, part (a) holds and the proof in this case follows.
![]() ${}_{\blacksquare }$
${}_{\blacksquare }$
Therefore, for the rest of the proof, we may suppose
Suppose that
![]() $|\mathcal {S}|\le 3|R|/4-|U|/2$
. From (16) and (17), we deduce
$|\mathcal {S}|\le 3|R|/4-|U|/2$
. From (16) and (17), we deduce
 $$ \begin{align*} \kappa&\le \mathbf{c}(R)-\left( \frac{|R|}{4}-\frac{|U|}{4}-\frac{3|R|}{16}+\frac{|U|}{8}\right)\\ &= \mathbf{c}(R)-\left( \frac{|R|}{16}-\frac{|U|}{8}\right)\\ &\le\mathbf{c}(R)-\left( \frac{|R|}{16}-\frac{|R|}{24}\right)=\mathbf{c}(R)- \frac{|R|}{48} \end{align*} $$
$$ \begin{align*} \kappa&\le \mathbf{c}(R)-\left( \frac{|R|}{4}-\frac{|U|}{4}-\frac{3|R|}{16}+\frac{|U|}{8}\right)\\ &= \mathbf{c}(R)-\left( \frac{|R|}{16}-\frac{|U|}{8}\right)\\ &\le\mathbf{c}(R)-\left( \frac{|R|}{16}-\frac{|R|}{24}\right)=\mathbf{c}(R)- \frac{|R|}{48} \end{align*} $$
and the proof in this case follows.
![]() ${}_{\blacksquare }$
${}_{\blacksquare }$
Therefore, for the rest of the proof, we suppose
To introduce the next case, we first need to make some general observations.
Let u be an arbitrary element of U. Then
![]() $u\mathcal {S}\subseteq R\setminus U$
and hence
$u\mathcal {S}\subseteq R\setminus U$
and hence
![]() $\mathcal {S}\cup u\mathcal {S}\subseteq R\setminus U$
. Therefore,
$\mathcal {S}\cup u\mathcal {S}\subseteq R\setminus U$
. Therefore,
 $$ \begin{align} |\mathcal{S}\cap u\mathcal{S}|&= |\mathcal{S}|+|u\mathcal{S}|-|\mathcal{S}\cup u\mathcal{S}|=2|\mathcal{S}|-|\mathcal{S}\cup u\mathcal{S}|\\ \nonumber &\ge 2|\mathcal{S}|-(|R|-|U|)>\frac{3|R|}{2}-|U|-(|R|-|U|)=\frac{|R|}{2}.\nonumber \end{align} $$
$$ \begin{align} |\mathcal{S}\cap u\mathcal{S}|&= |\mathcal{S}|+|u\mathcal{S}|-|\mathcal{S}\cup u\mathcal{S}|=2|\mathcal{S}|-|\mathcal{S}\cup u\mathcal{S}|\\ \nonumber &\ge 2|\mathcal{S}|-(|R|-|U|)>\frac{3|R|}{2}-|U|-(|R|-|U|)=\frac{|R|}{2}.\nonumber \end{align} $$
Now, let
![]() $ux\in \mathcal {S}\cap u\mathcal {S}$
. Then
$ux\in \mathcal {S}\cap u\mathcal {S}$
. Then
![]() $x\in \mathcal {S}$
, and hence
$x\in \mathcal {S}$
, and hence
Therefore,
![]() $u^x=u^{-1}$
. Now, repeating the argument above with
$u^x=u^{-1}$
. Now, repeating the argument above with
![]() $y\in \mathcal {S}\cap u\mathcal {S}$
, we deduce
$y\in \mathcal {S}\cap u\mathcal {S}$
, we deduce
![]() $u^y=u^{-1}$
and hence
$u^y=u^{-1}$
and hence
![]() $xy^{-1}\in \mathbf {C}_R(u)$
. Since we have
$xy^{-1}\in \mathbf {C}_R(u)$
. Since we have
![]() $|\mathcal {S}\cap u\mathcal {S}|$
choices for y, (18) implies
$|\mathcal {S}\cap u\mathcal {S}|$
choices for y, (18) implies
![]() $|\mathbf {C}_R(u)|>|R|/2$
and hence
$|\mathbf {C}_R(u)|>|R|/2$
and hence
![]() $R=\mathbf {C}_R(u)$
. Since u is an arbitrary element of U, we deduce that U is a central subgroup of R.
$R=\mathbf {C}_R(u)$
. Since u is an arbitrary element of U, we deduce that U is a central subgroup of R.
Since
![]() $u^x=u^{-1}$
, for every
$u^x=u^{-1}$
, for every
![]() $u\in U$
and for every
$u\in U$
and for every
![]() $ux\in \mathcal {S}\cap u\mathcal {S}$
, and since U is contained in the center of R, we deduce that U has exponent
$ux\in \mathcal {S}\cap u\mathcal {S}$
, and since U is contained in the center of R, we deduce that U has exponent
![]() $2$
. Since U is a central subgroup of R of exponent
$2$
. Since U is a central subgroup of R of exponent
![]() $2$
, we now have an easier description for
$2$
, we now have an easier description for
![]() $\mathcal {S}$
, that is,
$\mathcal {S}$
, that is,
Now that we know that U has exponent
![]() $2$
, we consider the quotient group
$2$
, we consider the quotient group
![]() ${\bar {R}:=R/\langle r\rangle }$
. Observe that each element of
${\bar {R}:=R/\langle r\rangle }$
. Observe that each element of
![]() $\bar U$
is an involution.
$\bar U$
is an involution.
Suppose that
![]() $\bar {R}$
is not an elementary abelian
$\bar {R}$
is not an elementary abelian
![]() $2$
-group. The theorem of Miller [Reference Miller16] yields
$2$
-group. The theorem of Miller [Reference Miller16] yields
![]() $|\mathbf {I}(\bar {R})|\le 3|\bar {R}|/4$
. In particular, the number of involutions in
$|\mathbf {I}(\bar {R})|\le 3|\bar {R}|/4$
. In particular, the number of involutions in
![]() $\bar {R}\setminus \bar {U}$
is at most
$\bar {R}\setminus \bar {U}$
is at most
![]() $3|\bar {R}|/4-|\bar {U}|$
. Since each element in
$3|\bar {R}|/4-|\bar {U}|$
. Since each element in
![]() $\bar {\mathcal {S}}$
is an involution and since
$\bar {\mathcal {S}}$
is an involution and since
![]() $\bar {\mathcal {S}}\subseteq \bar {R}\setminus \bar {U}$
, we deduce
$\bar {\mathcal {S}}\subseteq \bar {R}\setminus \bar {U}$
, we deduce
![]() $|\mathcal {S}|\le 3|R|/4-|U|$
. Using this inequality in (16), we get
$|\mathcal {S}|\le 3|R|/4-|U|$
. Using this inequality in (16), we get
part (a) holds and the proof follows in this case. It remains to consider the case that
![]() $\bar {R}$
is an elementary abelian
$\bar {R}$
is an elementary abelian
![]() $2$
-group.
$2$
-group.
Suppose that
![]() $\bar {R}$
is an elementary abelian
$\bar {R}$
is an elementary abelian
![]() $2$
-group. Recall that the Frattini subgroup
$2$
-group. Recall that the Frattini subgroup
![]() $\Phi (X)$
of a finite group X is the intersection of all the maximal subgroups of X. Recall also that, if X is a p-group for some prime p, then
$\Phi (X)$
of a finite group X is the intersection of all the maximal subgroups of X. Recall also that, if X is a p-group for some prime p, then
![]() $\Phi (X)=X^p[X,X]$
, where
$\Phi (X)=X^p[X,X]$
, where
![]() $[X,X]$
is the commutator subgroup of X and
$[X,X]$
is the commutator subgroup of X and
![]() $X^p:=\langle x^p\mid x\in X\rangle $
. When
$X^p:=\langle x^p\mid x\in X\rangle $
. When
![]() $p=2$
,
$p=2$
,
![]() $[X,X]\le X^2$
because
$[X,X]\le X^2$
because
![]() $X/X^2$
is abelian. Therefore,
$X/X^2$
is abelian. Therefore,
![]() $\Phi (X)=X^2$
.
$\Phi (X)=X^2$
.
Since the Frattini subgroup
![]() $\Phi (\bar {R})$
of
$\Phi (\bar {R})$
of
![]() $\bar {R}$
is the identity and since
$\bar {R}$
is the identity and since
![]() $r\in \Phi (R)$
, we deduce
$r\in \Phi (R)$
, we deduce
![]() $\Phi (R)=\langle r\rangle $
. Now, if R is abelian, then from the structure theorem of finitely generated abelian groups, we deduce that R is isomorphic to
$\Phi (R)=\langle r\rangle $
. Now, if R is abelian, then from the structure theorem of finitely generated abelian groups, we deduce that R is isomorphic to
-
(i)
 $C_4\times C_2^{\ell }$
for some
$C_4\times C_2^{\ell }$
for some
 $\ell \ge 0$
.
$\ell \ge 0$
.
If R is non-abelian, then
![]() $1\ne [R,R]\le \langle r\rangle $
and hence
$1\ne [R,R]\le \langle r\rangle $
and hence
![]() $[R,R]=\Phi (R)=\langle r\rangle $
. Now, from [Reference Berkovich4, Lemmas 4.2 and 4.3 and Remark 1, p. 74], we obtain that
$[R,R]=\Phi (R)=\langle r\rangle $
. Now, from [Reference Berkovich4, Lemmas 4.2 and 4.3 and Remark 1, p. 74], we obtain that
![]() $R=E\times A$
, where E is an extraspecial
$R=E\times A$
, where E is an extraspecial
![]() $2$
-group and A is an elementary abelian
$2$
-group and A is an elementary abelian
![]() $2$
-group. Now, from the structure theorem of extraspecial
$2$
-group. Now, from the structure theorem of extraspecial
![]() $2$
-groups [Reference Suzuki25, Theorem 4.18(ii)], we deduce that R is isomorphic to one of the following groups:
$2$
-groups [Reference Suzuki25, Theorem 4.18(ii)], we deduce that R is isomorphic to one of the following groups:
-
(ii)
 $\underbrace {D_8\circ D_8\circ \cdots \circ D_8}_{t\textrm { times}}\times C_2^{\ell }$
, for some
$\underbrace {D_8\circ D_8\circ \cdots \circ D_8}_{t\textrm { times}}\times C_2^{\ell }$
, for some
 $\ell \ge 0$
and
$\ell \ge 0$
and
 $t\ge 1$
.
$t\ge 1$
. -
(iii)
 $Q_8\circ \underbrace {D_8\circ D_8\circ \cdots \circ D_8}_{(t-1)\textrm { times}}\times C_2^{\ell }$
, for some
$Q_8\circ \underbrace {D_8\circ D_8\circ \cdots \circ D_8}_{(t-1)\textrm { times}}\times C_2^{\ell }$
, for some
 $\ell \ge 0$
and some
$\ell \ge 0$
and some
 $t\ge 1$
.
$t\ge 1$
. -
(iv)
 $C_4\circ \underbrace {D_8\circ D_8\circ \cdots \circ D_8}_{t\textrm { times}}\times C_2^{\ell }$
, for some
$C_4\circ \underbrace {D_8\circ D_8\circ \cdots \circ D_8}_{t\textrm { times}}\times C_2^{\ell }$
, for some
 $\ell \ge 0$
and some
$\ell \ge 0$
and some
 $t\ge 1$
.
$t\ge 1$
.
Therefore, the case that
![]() $\bar {R}$
is elementary abelian splits naturally into four cases. To conclude the proof of this lemma, we look at each case in detail.
$\bar {R}$
is elementary abelian splits naturally into four cases. To conclude the proof of this lemma, we look at each case in detail.
In Case (i), an explicit computation gives
![]() $|\mathcal {S}|=|R|/2$
. Hence, (16) gives
$|\mathcal {S}|=|R|/2$
. Hence, (16) gives
 $$ \begin{align*} \kappa&\le\mathbf{c}(R)-\left(\frac{|R|}{4}-\frac{|U|}{4}-\frac{|R|}{8}\right)= \mathbf{c}(R)-\left(\frac{|R|}{8}-\frac{|U|}{4}\right)\\ &\le\mathbf{c}(R)-\left(\frac{|R|}{8}-\frac{|R|}{16}\right) =\mathbf{c}(R)-\frac{|R|}{16} \end{align*} $$
$$ \begin{align*} \kappa&\le\mathbf{c}(R)-\left(\frac{|R|}{4}-\frac{|U|}{4}-\frac{|R|}{8}\right)= \mathbf{c}(R)-\left(\frac{|R|}{8}-\frac{|U|}{4}\right)\\ &\le\mathbf{c}(R)-\left(\frac{|R|}{8}-\frac{|R|}{16}\right) =\mathbf{c}(R)-\frac{|R|}{16} \end{align*} $$
and part (a) holds.
In Case (ii), an explicit computation gives
![]() $|\mathcal {S}|=(2^t-1)|R|/2^{t+1}\le |R|/2$
. Therefore, we may argue as in the previous case and we obtain that part (a) holds.
$|\mathcal {S}|=(2^t-1)|R|/2^{t+1}\le |R|/2$
. Therefore, we may argue as in the previous case and we obtain that part (a) holds.
In Case (iii), an explicit computation gives
![]() $|\mathcal {S}|=(2^t+1)|R|/2^{t+1}$
. When
$|\mathcal {S}|=(2^t+1)|R|/2^{t+1}$
. When
![]() $t=1$
,
$t=1$
,
![]() ${R\cong Q_8\times C_2^{\ell }}$
is generalized dicyclic and hence part (b) hods. When
${R\cong Q_8\times C_2^{\ell }}$
is generalized dicyclic and hence part (b) hods. When
![]() $t\ge 2$
, we have
$t\ge 2$
, we have
![]() ${|\mathcal {S}|\le 5|R|/8}$
and hence (16) gives
${|\mathcal {S}|\le 5|R|/8}$
and hence (16) gives
 $$ \begin{align*} \kappa&\le\mathbf{c}(R)-\left(\frac{|R|}{4}-\frac{|U|}{4}-\frac{5|R|}{32}\right)= \mathbf{c}(R)-\left(\frac{3|R|}{32}-\frac{|U|}{4}\right)\\ &\le\mathbf{c}(R)-\left(\frac{3|R|}{32}-\frac{|R|}{16}\right) =\mathbf{c}(R)-\frac{|R|}{32}. \end{align*} $$
$$ \begin{align*} \kappa&\le\mathbf{c}(R)-\left(\frac{|R|}{4}-\frac{|U|}{4}-\frac{5|R|}{32}\right)= \mathbf{c}(R)-\left(\frac{3|R|}{32}-\frac{|U|}{4}\right)\\ &\le\mathbf{c}(R)-\left(\frac{3|R|}{32}-\frac{|R|}{16}\right) =\mathbf{c}(R)-\frac{|R|}{32}. \end{align*} $$
Thus, we obtain that part (a) holds.
In Case (iv), an explicit computation gives
![]() $|\mathcal {S}|=|R|/2$
. Therefore, we may argue as in the first case and we obtain that part (a) holds.
$|\mathcal {S}|=|R|/2$
. Therefore, we may argue as in the first case and we obtain that part (a) holds.
3 Proof of Theorems 1.1 and 1.2
In this section, using Section 2, we prove both Theorems 1.1 and 1.2. Thus, let G be a finite transitive permutation group on
![]() $\Omega $
with
$\Omega $
with
If
![]() $\mathbf {I}_{\Omega }(G)=1$
, then there is nothing to prove and hence we may suppose that
$\mathbf {I}_{\Omega }(G)=1$
, then there is nothing to prove and hence we may suppose that
![]() $\mathbf {I}_{\Omega }(G)<1$
. Let
$\mathbf {I}_{\Omega }(G)<1$
. Let
![]() $\alpha \in \Omega $
. From Lemma 2.1, we have
$\alpha \in \Omega $
. From Lemma 2.1, we have
Since
![]() $\mathbf {I}_{\Omega }(G)<1$
,
$\mathbf {I}_{\Omega }(G)<1$
,
![]() $\Omega _{\alpha ,4}\ne \emptyset $
. Let
$\Omega _{\alpha ,4}\ne \emptyset $
. Let
![]() $\beta \in \Omega _{\alpha ,4}$
. From Lemma 2.5,
$\beta \in \Omega _{\alpha ,4}$
. From Lemma 2.5,
is an elementary abelian normal
![]() $2$
-subgroup of G of order
$2$
-subgroup of G of order
![]() $16$
. Let
$16$
. Let
![]() $e_1,e_2,e_3,e_4$
be a basis of V, regarded as a vector space over the field with two elements, and with
$e_1,e_2,e_3,e_4$
be a basis of V, regarded as a vector space over the field with two elements, and with
![]() $G_{\alpha }=\langle e_1,e_2\rangle $
. Let
$G_{\alpha }=\langle e_1,e_2\rangle $
. Let
![]() $H:=G/\mathbf {C}_G(V)$
and
$H:=G/\mathbf {C}_G(V)$
and
![]() $W:=G_{\alpha }$
. Clearly,
$W:=G_{\alpha }$
. Clearly,
![]() $H\le \mathrm {GL}(V)\cong \mathrm {GL}_4(2)$
. Now, consider the action of H on the two-dimensional subspaces of V and consider
$H\le \mathrm {GL}(V)\cong \mathrm {GL}_4(2)$
. Now, consider the action of H on the two-dimensional subspaces of V and consider
![]() ${O:=\{W^h\mid h\in H\}}$
, the H-orbit containing W. Clearly,
${O:=\{W^h\mid h\in H\}}$
, the H-orbit containing W. Clearly,
 $$ \begin{align*} \frac{|\Omega_{\alpha,1}\cup\Omega_{\alpha,2}|}{|\Omega|}=\frac{|\{U\in O\mid |W:W\cap U|\le 2\}|}{|O|}. \end{align*} $$
$$ \begin{align*} \frac{|\Omega_{\alpha,1}\cup\Omega_{\alpha,2}|}{|\Omega|}=\frac{|\{U\in O\mid |W:W\cap U|\le 2\}|}{|O|}. \end{align*} $$
Observe that the right-hand side of this equality can be easily computed with the help of a computer. With the computer algebra system magma [Reference Bosma, Cannon and Playoust5], we have computed all the subgroups of
![]() $\mathrm {GL}_4(2)$
. Then, we have selected only the subgroups H with the property that
$\mathrm {GL}_4(2)$
. Then, we have selected only the subgroups H with the property that
(This selection is due to the fact that
![]() $V=\langle G_{\alpha }^g\mid g\in G\rangle $
and that
$V=\langle G_{\alpha }^g\mid g\in G\rangle $
and that
![]() $G_{\alpha }$
is core-free in G.) Then, for each such subgroup H, we have computed the orbit
$G_{\alpha }$
is core-free in G.) Then, for each such subgroup H, we have computed the orbit
![]() $O=W^H$
and we have computed the ratio
$O=W^H$
and we have computed the ratio
![]() $\frac {|\{U\in O\mid |W:W\cap U|\le 2\}|}{|O|}$
. We have checked that in all cases, this ratio is at most
$\frac {|\{U\in O\mid |W:W\cap U|\le 2\}|}{|O|}$
. We have checked that in all cases, this ratio is at most
![]() $5/6$
. In particular, Theorem 1.1 is proved. Moreover, we have checked that this ratio is
$5/6$
. In particular, Theorem 1.1 is proved. Moreover, we have checked that this ratio is
![]() $5/6$
if and only if H is given in the statement of Theorem 1.2. (We are including in the Appendix, the code required to perform this computation with the computer algebra system magma.) Since this construction can be reversed, we also obtain the converse implication for Theorem 1.2.
$5/6$
if and only if H is given in the statement of Theorem 1.2. (We are including in the Appendix, the code required to perform this computation with the computer algebra system magma.) Since this construction can be reversed, we also obtain the converse implication for Theorem 1.2.
4 Proof of Theorem 1.9
Let G be a finite transitive group properly containing a regular subgroup R. Since R acts regularly, we may identify the domain of G with R. Now, the number of Cayley graphs
![]() $\mathop {\Gamma }(R,S)$
on R with
$\mathop {\Gamma }(R,S)$
on R with
![]() $G\le \mathrm {Aut}(\mathop {\Gamma }(R,S))$
is the number of inverse-closed subsets S of R left invariant by
$G\le \mathrm {Aut}(\mathop {\Gamma }(R,S))$
is the number of inverse-closed subsets S of R left invariant by
![]() $G_1$
, where
$G_1$
, where
![]() $G_1$
is the stabilizer of the point
$G_1$
is the stabilizer of the point
![]() $1\in R$
in G. In particular, to prove Theorem 1.9, we need to estimate the number of inverse-closed subsets of R that are union of
$1\in R$
in G. In particular, to prove Theorem 1.9, we need to estimate the number of inverse-closed subsets of R that are union of
![]() $G_1$
-orbits.
$G_1$
-orbits.
Suppose first that
Since R is properly contained in G, from the theorem of Bergman and Lenstra mentioned in Section 1, we have two cases to consider:
-
•
 $|G_1|=2$
.
$|G_1|=2$
. -
• G contains an elementary abelian normal
 $2$
-subgroup N with
$2$
-subgroup N with
 $|N:G_1|=2$
.
$|N:G_1|=2$
.
Assume first that
![]() $|G_1|=2$
. Let
$|G_1|=2$
. Let
![]() $\varphi \in G_1\setminus \{1\}$
. From the Frattini argument,
$\varphi \in G_1\setminus \{1\}$
. From the Frattini argument,
![]() $G=RG_1$
and hence
$G=RG_1$
and hence
![]() $|G:R|=2$
. This gives
$|G:R|=2$
. This gives
![]() $R\unlhd G$
and hence
$R\unlhd G$
and hence
![]() $\varphi $
acts by conjugation on R as a group automorphism. Now, from [Reference Spiga24, Lemma
$\varphi $
acts by conjugation on R as a group automorphism. Now, from [Reference Spiga24, Lemma
![]() $2.7$
] or [Reference Morris, Moscatiello and Spiga17, Theorem 1.13], we have that:
$2.7$
] or [Reference Morris, Moscatiello and Spiga17, Theorem 1.13], we have that:
-
(a) The number of
 $\varphi $
-invariant inverse-closed subsets of R is at most
$\varphi $
-invariant inverse-closed subsets of R is at most
 $2^{\mathbf { c}(R)-\frac {|R|}{96}}$
, or
$2^{\mathbf { c}(R)-\frac {|R|}{96}}$
, or -
(b) R is abelian of exponent greater than
 $2$
and
$2$
and
 $\varphi $
is the automorphism of R mapping each element to its inverse, or
$\varphi $
is the automorphism of R mapping each element to its inverse, or -
(c) R is generalized dicyclic and
 $\varphi $
is an automorphism of R with
$\varphi $
is an automorphism of R with
 $x^{\varphi }\in \{x,x^{-1}\}$
, for every
$x^{\varphi }\in \{x,x^{-1}\}$
, for every
 $x\in R$
.
$x\in R$
.
In particular, the proof of Theorem 1.9 follows in this case.
Assume next that G contains an elementary abelian normal
![]() $2$
-subgroup N with
$2$
-subgroup N with
![]() $|N:G_1|=2$
. Since R acts transitively,
$|N:G_1|=2$
. Since R acts transitively,
![]() $G=RN$
. Moreover, since R acts regularly,
$G=RN$
. Moreover, since R acts regularly,
![]() ${G=RG_1}$
and
${G=RG_1}$
and
![]() $R\cap G_1=1$
. Thus
$R\cap G_1=1$
. Thus
![]() $|R\cap N|=|N|/|G_1|=2$
. Let r be a generator of
$|R\cap N|=|N|/|G_1|=2$
. Let r be a generator of
![]() $R\cap N$
. Since
$R\cap N$
. Since
![]() ${\langle r\rangle =R\cap N\unlhd R}$
, r is a central involution of R. Let
${\langle r\rangle =R\cap N\unlhd R}$
, r is a central involution of R. Let
![]() $U:=\mathbf {N}_R(G_1)$
. Since
$U:=\mathbf {N}_R(G_1)$
. Since
![]() $\mathbf {N}_R(G_1)$
is a block of imprimitivity for G,
$\mathbf {N}_R(G_1)$
is a block of imprimitivity for G,
![]() $U=\mathbf {N}_R(G_1)$
is also a block of imprimitivity for the regular action of R and hence U is a subgroup of R. As
$U=\mathbf {N}_R(G_1)$
is also a block of imprimitivity for the regular action of R and hence U is a subgroup of R. As
![]() $G_1\ne 1 $
because R is properly contained in G, we deduce that U is a proper subgroup of R. Now,
$G_1\ne 1 $
because R is properly contained in G, we deduce that U is a proper subgroup of R. Now,
![]() $G_1$
fixes pointwise U and, for every
$G_1$
fixes pointwise U and, for every
![]() $x\in R\setminus U$
, we have
$x\in R\setminus U$
, we have
Let
![]() $\tau :R\to R$
be the permutation defined by
$\tau :R\to R$
be the permutation defined by
 $$ \begin{align*} x\mapsto x^{\tau}:= \begin{cases} x,&\textrm{when }x\in U,\\ xr,&\textrm{when }x\in R\setminus U. \end{cases} \end{align*} $$
$$ \begin{align*} x\mapsto x^{\tau}:= \begin{cases} x,&\textrm{when }x\in U,\\ xr,&\textrm{when }x\in R\setminus U. \end{cases} \end{align*} $$
We have shown that
![]() $S\subseteq R$
is
$S\subseteq R$
is
![]() $G_1$
-invariant if and only if S is
$G_1$
-invariant if and only if S is
![]() $\langle \tau \rangle $
-invariant. Therefore, the proof of this case follows from Lemma 2.6.
$\langle \tau \rangle $
-invariant. Therefore, the proof of this case follows from Lemma 2.6.
To conclude the proof of Theorem 1.9, it remains to consider the case that
From Theorem 1.1, we have
![]() $\mathbf {I}_R(G)\le 5/6$
. Recall that
$\mathbf {I}_R(G)\le 5/6$
. Recall that
![]() $\mathbf { I}(R)=\{x\in R\mid x^2=1\}.$
We define
$\mathbf { I}(R)=\{x\in R\mid x^2=1\}.$
We define
 $$ \begin{align*} &a:=|\Omega_{R,1}\cap \mathbf{I}(R)|,&&b:=|\Omega_{R,1}\cap (R\setminus \mathbf{I}(R))|,\\ &c:=|\Omega_{R,2}\cap \mathbf{I}(R)|,&&d:=|\Omega_{R,2}\cap (R\setminus \mathbf{I}(R))|,\\ e&:=|(R\setminus (\Omega_{R,1}\cup \Omega_{R,2}))\cap \mathbf{I}(R)|,&&f:=|(R\setminus (\Omega_{R,1}\cup \Omega_{R,2}))\cap (R\setminus \mathbf{I}(R))|. \end{align*} $$
$$ \begin{align*} &a:=|\Omega_{R,1}\cap \mathbf{I}(R)|,&&b:=|\Omega_{R,1}\cap (R\setminus \mathbf{I}(R))|,\\ &c:=|\Omega_{R,2}\cap \mathbf{I}(R)|,&&d:=|\Omega_{R,2}\cap (R\setminus \mathbf{I}(R))|,\\ e&:=|(R\setminus (\Omega_{R,1}\cup \Omega_{R,2}))\cap \mathbf{I}(R)|,&&f:=|(R\setminus (\Omega_{R,1}\cup \Omega_{R,2}))\cap (R\setminus \mathbf{I}(R))|. \end{align*} $$
As
![]() $\mathbf {I}_R(G)\le 5/6$
, we deduce
$\mathbf {I}_R(G)\le 5/6$
, we deduce
Let
![]() $\iota :R\to R$
be the permutation defined by
$\iota :R\to R$
be the permutation defined by
![]() $x^{\iota }:=x^{-1}$
, for every
$x^{\iota }:=x^{-1}$
, for every
![]() $x\in R$
, and let
$x\in R$
, and let
![]() ${T:=\langle \iota ,G_1\rangle }$
. Now, the number of
${T:=\langle \iota ,G_1\rangle }$
. Now, the number of
![]() $G_1$
-invariant inverse-closed subsets of R is exactly the number of T-invariant subsets of R. Moreover, the number of T-invariant subsets of R is
$G_1$
-invariant inverse-closed subsets of R is exactly the number of T-invariant subsets of R. Moreover, the number of T-invariant subsets of R is
![]() $2^{\kappa }$
, where
$2^{\kappa }$
, where
![]() $\kappa $
is the number of orbits of T on R.
$\kappa $
is the number of orbits of T on R.
The group T has:
-
• Orbits of cardinality
 $1$
on
$1$
on
 $\Omega _{R,1}\cap \mathbf {I}(R)$
.
$\Omega _{R,1}\cap \mathbf {I}(R)$
. -
• Orbits of cardinality
 $2$
on
$2$
on
 $\Omega _{R,1}\cap (R\setminus \mathbf {I}(R))$
.
$\Omega _{R,1}\cap (R\setminus \mathbf {I}(R))$
. -
• Orbits of cardinality
 $2$
on
$2$
on
 $\Omega _{R,2}\cap \mathbf {I}(R)$
.
$\Omega _{R,2}\cap \mathbf {I}(R)$
. -
• Orbits of cardinality at least
 $2$
on
$2$
on
 $\Omega _{R,2}\cap (R\setminus \mathbf {I}(R))$
.
$\Omega _{R,2}\cap (R\setminus \mathbf {I}(R))$
. -
• Orbits of cardinality at least
 $3$
on
$3$
on
 $(R\setminus (\Omega _{R,1}\cup \Omega _{R,2}))\cap \mathbf {I}(R)$
.
$(R\setminus (\Omega _{R,1}\cup \Omega _{R,2}))\cap \mathbf {I}(R)$
. -
• Orbits of cardinality at least
 $4$
on
$4$
on
 $(R\setminus (\Omega _{R,1}\cup \Omega _{R,2}))\cap (R\setminus \mathbf { I}(R))$
.
$(R\setminus (\Omega _{R,1}\cup \Omega _{R,2}))\cap (R\setminus \mathbf { I}(R))$
.
All of these assertions are trivial except, possibly, the last one. Indeed, if
![]() $x\in (R\setminus (\Omega _{R,1}\cup \Omega _{R,2}))\cap (R\setminus \mathbf {I}(R))$
, then x is not an involution and the
$x\in (R\setminus (\Omega _{R,1}\cup \Omega _{R,2}))\cap (R\setminus \mathbf {I}(R))$
, then x is not an involution and the
![]() $G_1$
-orbit
$G_1$
-orbit
![]() $x^{G_1}$
has cardinality at least
$x^{G_1}$
has cardinality at least
![]() $3$
. As
$3$
. As
we deduce that
![]() $|x^T|$
has even cardinality and hence
$|x^T|$
has even cardinality and hence
![]() $|x^T|$
is at least
$|x^T|$
is at least
![]() $4$
.
$4$
.
Summing up, we have
 $$ \begin{align*} \kappa&\le a+\frac{b}{2}+\frac{c}{2}+\frac{d}{2}+\frac{e}{3}+\frac{f}{4}=a+c+e+\frac{b}{2}+\frac{d}{2}+\frac{f}{2}-\left(\frac{c}{2}+\frac{2e}{3}+\frac{f}{4}\right)\\ &=\frac{|R|+|\mathbf{I}(R)|}{2}-\left(\frac{c}{2}+\frac{2e}{3}+\frac{f}{4}\right) =\mathbf{c}(R)-\left(\frac{c}{2}+\frac{2e}{3}+\frac{f}{4}\right)\\ &\le\mathbf{c}(R)-\left(\frac{2e}{3}+\frac{f}{4}\right)\le \mathbf{c}(R)-\left(\frac{e}{4}+\frac{f}{4}\right)\\ &\le\mathbf{c}(R)-\frac{|R|}{24}, \end{align*} $$
$$ \begin{align*} \kappa&\le a+\frac{b}{2}+\frac{c}{2}+\frac{d}{2}+\frac{e}{3}+\frac{f}{4}=a+c+e+\frac{b}{2}+\frac{d}{2}+\frac{f}{2}-\left(\frac{c}{2}+\frac{2e}{3}+\frac{f}{4}\right)\\ &=\frac{|R|+|\mathbf{I}(R)|}{2}-\left(\frac{c}{2}+\frac{2e}{3}+\frac{f}{4}\right) =\mathbf{c}(R)-\left(\frac{c}{2}+\frac{2e}{3}+\frac{f}{4}\right)\\ &\le\mathbf{c}(R)-\left(\frac{2e}{3}+\frac{f}{4}\right)\le \mathbf{c}(R)-\left(\frac{e}{4}+\frac{f}{4}\right)\\ &\le\mathbf{c}(R)-\frac{|R|}{24}, \end{align*} $$
where in the last inequality we have used (19). This concludes the proof of Theorem 1.9.
A Appendix
We report here the code used in the last paragraph of the proof of Theorem 1.2. We have performed the computations in the computer algebra system magma, and hence we present the code in this language. The code runs just under 4 minutes in the author’s personal laptop.