Article contents
Face Ring Multiplicity via CM-Connectivity Sequences
Published online by Cambridge University Press: 20 November 2018
Abstract
The multiplicity conjecture of Herzog, Huneke, and Srinivasan is verified for the face rings of the following classes of simplicial complexes: matroid complexes, complexes of dimension one and two, and Gorenstein complexes of dimension at most four. The lower bound part of this conjecture is also established for the face rings of all doubly Cohen–Macaulay complexes whose 1-skeleton's connectivity does not exceed the codimension plus one as well as for all 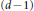 $\text{(}d-1)$-dimensional
$\text{(}d-1)$-dimensional  $d$-Cohen–Macaulay complexes. The main ingredient of the proofs is a new interpretation of the minimal shifts in the resolution of the face ring
$d$-Cohen–Macaulay complexes. The main ingredient of the proofs is a new interpretation of the minimal shifts in the resolution of the face ring 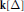 $\mathbf{k}[\Delta ]$ via the Cohen–Macaulay connectivity of the skeletons of
$\mathbf{k}[\Delta ]$ via the Cohen–Macaulay connectivity of the skeletons of  $\Delta $.
$\Delta $.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
- 6
- Cited by


