Article contents
Explicit Models for Threefolds Fibred by K3 Surfaces of Degree Two
Published online by Cambridge University Press: 20 November 2018
Abstract
We consider threefolds that admit a fibration by 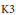 $\text{K3}$ surfaces over a nonsingular curve, equipped with a divisorial sheaf that defines a polarization of degree two on the general fibre. Under certain assumptions on the threefold we show that its relative log canonical model exists and can be explicitly reconstructed from a small set of data determined by the original fibration. Finally, we prove a converse to this statement: under certain assumptions, any such set of data determines a threefold that arises as the relative log canonical model of a threefold admitting a fibration by
$\text{K3}$ surfaces over a nonsingular curve, equipped with a divisorial sheaf that defines a polarization of degree two on the general fibre. Under certain assumptions on the threefold we show that its relative log canonical model exists and can be explicitly reconstructed from a small set of data determined by the original fibration. Finally, we prove a converse to this statement: under certain assumptions, any such set of data determines a threefold that arises as the relative log canonical model of a threefold admitting a fibration by 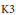 $\text{K3}$ surfaces of degree two.
$\text{K3}$ surfaces of degree two.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 1
- Cited by


