Hostname: page-component-7bb8b95d7b-pwrkn Total loading time: 0 Render date: 2024-09-20T08:51:53.696Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansion of Continuous Differentiable Functions in Fourier Legendre Series

Published online by Cambridge University Press:  20 November 2018

R. B. Saxena
R. B. Saxena*
Affiliation:
University of Alberta, Edmonton
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let

1.1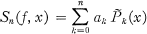

denote the nth partial sum of the Fourier Legendre series of a function ƒ(x). The references available to us, except (5), prove only that Sn(ƒ, x) converges uniformly to ƒ(x) in [— 1, 1] if ƒ(x) has a continuous second derivative on [—1, 1]. Very recently Suetin (5) has shown by employing a theorem of A. F. Timan (7) (which is a stronger form of Jackson's theorem) that Sn(ƒ, x) converges uniformly to ƒ(x) ƒ(x) belongs to a Lipschitz class of order greater than 1/2 in [—1, 1]. More generally he has proved the following theorem.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 823 - 827
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Dzyadyk, V. K., Constructive characterisation of functions satisfying the condition, Lip α. (0 < α < 1) on a finite segment of real axis (in Russian), Izv. Akad. Nauk SSSR, 20 (1956), 623–642.Google Scholar
2. Natanson, I. P., Constructive theory of functions (in Russian: GITTL, Moscow, 1949; English transi.: FUPC, New York, 1964).Google Scholar
3. Sansone, G., Orthogonal functions (in Italian; English transi., IPI, New York, 1959).Google Scholar
4. Saxena, R. B., On mixed type lacunary interpolation, II, Acta Math. Acad. Sci. Hungar., 14 (1963), 1–19.Google Scholar
5. Suetin, P. K., Representation of continuous and differentiate functions by Fourier series of Legendre polynomials, Soviet Math. Dokl., 5 (1964), 1408–1410.Google Scholar
6. Szegö, G., Orthogonal polynomials, Amer. Math. Soc. Colloq. Pub., 2nd ed. (1959).Google Scholar
7. Timan, A. F., Theory of approximation of functions of a real variable (English transi.: Fizmatgiz, Moscow, 1960).Google Scholar