Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Iyama, Osamu
2007.
Auslander correspondence.
Advances in Mathematics,
Vol. 210,
Issue. 1,
p.
51.
Toda, Yukinobu
and
Yasuda, Takehiko
2009.
Noncommutative resolution, F-blowups and D-modules.
Advances in Mathematics,
Vol. 222,
Issue. 1,
p.
318.
Buchweitz, Ragnar-Olaf
Leuschke, Graham J.
and
Van den Bergh, Michel
2010.
Non-commutative desingularization of determinantal varieties I.
Inventiones mathematicae,
Vol. 182,
Issue. 1,
p.
47.
Dao, Hailong
2010.
Remarks on non-commutative crepant resolutions of complete intersections.
Advances in Mathematics,
Vol. 224,
Issue. 3,
p.
1021.
Beligiannis, Apostolos
2011.
On algebras of finite Cohen–Macaulay type.
Advances in Mathematics,
Vol. 226,
Issue. 2,
p.
1973.
Yasuda, Takehiko
2012.
Pure subrings of regular local rings, endomorphism rings and Frobenius morphisms.
Journal of Algebra,
Vol. 370,
Issue. ,
p.
15.
Vasconcelos, Wolmer V.
2014.
On the radical of endomorphism rings of local modules.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 45,
Issue. 4,
p.
871.
Dao, Hailong
Faber, Eleonore
and
Ingalls, Colin
2015.
Noncommutative (Crepant) Desingularizations and the Global Spectrum of Commutative Rings.
Algebras and Representation Theory,
Vol. 18,
Issue. 3,
p.
633.
Doherty, Brandon
Faber, Eleonore
and
Ingalls, Colin
2016.
Computing global dimension of endomorphism rings via ladders.
Journal of Algebra,
Vol. 458,
Issue. ,
p.
307.
Holm, Henrik
2016.
The Category of Maximal Cohen–Macaulay Modules as a Ring with Several Objects.
Mediterranean Journal of Mathematics,
Vol. 13,
Issue. 3,
p.
885.
Puthenpurakal, Tony J.
2017.
Examples of non-commutative crepant resolutions of Cohen Macaulay normal domains.
Journal of Algebra,
Vol. 485,
Issue. ,
p.
77.
Zhang, Pu
2018.
Categorical resolutions of a class of derived categories.
Science China Mathematics,
Vol. 61,
Issue. 2,
p.
391.
Eshraghi, Hossein
2018.
Representation dimension via tilting theory.
Journal of Algebra,
Vol. 494,
Issue. ,
p.
77.
Flores, Zachary
2020.
G-Groups of Cohen-Macaulay Rings with n-Cluster Tilting Objects.
Algebras and Representation Theory,
Vol. 23,
Issue. 3,
p.
887.
Dugas, Alex S.
and
Leuschke, Graham J.
2021.
Some extensions of theorems of Knörrer and Herzog–Popescu.
Journal of Algebra,
Vol. 571,
Issue. ,
p.
94.
Kobayashi, Toshinori
2022.
Syzygies of Cohen–Macaulay Modules over One Dimensional Cohen–Macaulay Local Rings.
Algebras and Representation Theory,
Vol. 25,
Issue. 5,
p.
1061.
He, Ji-Wei
and
Ye, Yu
2022.
Preresolutions of noncommutative isolated singularities.
Pacific Journal of Mathematics,
Vol. 316,
Issue. 2,
p.
367.
Liedtke, Christian
and
Yasuda, Takehiko
2024.
Non-commutative resolutions of linearly reductive quotient singularities.
The Quarterly Journal of Mathematics,
Vol. 75,
Issue. 3,
p.
969.
Korell, Philipp
2024.
GORENSTEIN ENDOMORPHISM RINGS ON CURVE SINGULARITIES.
Journal of Commutative Algebra,
Vol. 16,
Issue. 1,
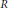 $R$, consider (noncommutative)
$R$, consider (noncommutative) 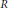 $R$-algebras
$R$-algebras  $\Lambda$ of the form
$\Lambda$ of the form 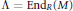 $\Lambda \,=\,\text{En}{{\text{d}}_{R}}\left( M \right)$ where
$\Lambda \,=\,\text{En}{{\text{d}}_{R}}\left( M \right)$ where 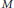 $M$ is a reflexive
$M$ is a reflexive 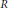 $R$-module with nonzero free direct summand. Such algebras
$R$-module with nonzero free direct summand. Such algebras  $\Lambda$ of finite global dimension can be viewed as potential substitutes for, or analogues of, a resolution of singularities of Spec
$\Lambda$ of finite global dimension can be viewed as potential substitutes for, or analogues of, a resolution of singularities of Spec 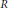 $R$. For example, Van den Bergh has shown that a three-dimensional Gorenstein normal
$R$. For example, Van den Bergh has shown that a three-dimensional Gorenstein normal  $\mathbb{C}$-algebra with isolated terminal singularities has a crepant resolution of singularities if and only if it has such an algebra
$\mathbb{C}$-algebra with isolated terminal singularities has a crepant resolution of singularities if and only if it has such an algebra  $\Lambda$ with finite global dimension and which is maximal Cohen-Macaulay over
$\Lambda$ with finite global dimension and which is maximal Cohen-Macaulay over 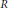 $R$ (a “noncommutative crepant resolution of singularities”). We produce algebras
$R$ (a “noncommutative crepant resolution of singularities”). We produce algebras 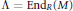 $\Lambda \,=\,\text{En}{{\text{d}}_{R}}\left( M \right) $ having finite global dimension in two contexts: when
$\Lambda \,=\,\text{En}{{\text{d}}_{R}}\left( M \right) $ having finite global dimension in two contexts: when 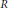 $R$ is a reduced one-dimensional complete local ring, or when
$R$ is a reduced one-dimensional complete local ring, or when 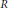 $R$ is a Cohen-Macaulay local ring of finite Cohen–Macaulay type. If in the latter case
$R$ is a Cohen-Macaulay local ring of finite Cohen–Macaulay type. If in the latter case 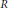 $R$ is Gorenstein, then the construction gives a noncommutative crepant resolution of singularities in the sense of Van den Bergh.
$R$ is Gorenstein, then the construction gives a noncommutative crepant resolution of singularities in the sense of Van den Bergh.

