Hostname: page-component-5c6d5d7d68-wpx84 Total loading time: 0 Render date: 2024-08-18T19:00:51.042Z Has data issue: false hasContentIssue false
  • English
  • Français

Differences, Derivatives, and Decreasing Rearrangements

Published online by Cambridge University Press:  20 November 2018

G. F. D. Duff
G. F. D. Duff*
Affiliation:
University of Toronto
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The decreasing rearrangement of a finite sequence a1, a2, … , an of real numbers is a second sequence aπ(1), aπ(2), … , aπ(n), where π(l), π(2), … , π(n) is a permutation of 1, 2, … , n and

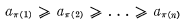
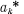(1, p. 260). The kth term of the rearranged sequence will be denoted by . Thus the terms of the rearranged sequence 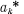correspond to and are equal to those of the given sequence ak, but are arranged in descending (non-increasing) order.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 1153 - 1178
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Hardy, G. H., Littlewood, J. E., and Polya, G., Inequalities, 2nd ed. (Cambridge, 1952).Google Scholar
2. Kamke, E., Theory of sets (translated; New York, 1950).Google Scholar
3. Riesz, F. and Sz, B.. Nagy, Functional analysis (translated; London, 1955).Google Scholar
4. Titchmarsh, E. C., Theory of functions, 2nd ed. (Oxford, 1939).Google Scholar