Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-23T17:20:44.570Z Has data issue: false hasContentIssue false
  • English
  • Français

Complexes Over a Complete Algebra of Quotients

Published online by Cambridge University Press:  20 November 2018

Krishna Tewari
Krishna Tewari*
Affiliation:
Indian Institute of Technology, Kanpur (U.P.), India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a commutative ring with unit and A be a unitary commutative R-algebra. Let As be a generalized algebra of quotients of A with respect to a multiplicatively closed subset S of A. If 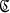(A) and 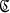(As) denote the categories of complexes and their homomorphisms over A and As respectively, then one easily sees that there exists a covariant functor T: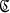(A) → 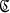(AS) such that T is onto and T(X, d) is universal over As whenever (X, d) is universal over A. Actually the category 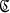(AS) is equivalent to a subcategory 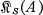of 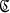(A) where 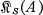contains all those complexes (X, d) over A such that for each s in S, the module homomorphism ϕs: x → sx of Xn into itself is one-one and onto for each n ⩾ 1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 40 - 57
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Bourbaki, N., Algèbre commutative, Chap. I (Paris, 1961).Google Scholar
2. Bourbaki, N., Algèbre, Chap. II (Paris, 1955).Google Scholar
3. Cartan, H. and Eilenberg, S., Homologuai algebra (Princeton, 1956).Google Scholar
4. Chevalley, C., Fundamental concepts of algebra (New York), 1956.Google Scholar
5. Kähler, E., Algebra und Differentialrechnung Bericht über die Mathematiker-Tagung in Berlin vom 14. bis 18. Januar 1953 (Berlin, 1954).Google Scholar
6. Lambek, J., On the structure of semi-prime rings and their rings of quotients, Can. J. Math., 13 (1961), 392–417.Google Scholar