Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yamada, Masahiro
1999.
Carleson inequalities in classes of derivatives of harmonic Bergman functions with $0<płeq 1$.
Hiroshima Mathematical Journal,
Vol. 29,
Issue. 1,
Chen, Zeqian
2003.
Characterizations of Arveson's Hardy Space.
Complex Variables, Theory and Application: An International Journal,
Vol. 48,
Issue. 5,
p.
453.
Cascante, Carme
and
Ortega, Joaquin M.
2003.
Imbedding potentials in tent spaces.
Journal of Functional Analysis,
Vol. 198,
Issue. 1,
p.
106.
Hu, Peng Yan
and
Zhang, Wen Jun
2004.
Small Hankel Operators on the Dirichlet-Type Spaces on the Unit Ball of C n.
Acta Mathematica Sinica, English Series,
Vol. 20,
Issue. 2,
p.
261.
Cascante, Carme
and
Ortega, Joaquin M.
2007.
Carleson measures for weighted Hardy-sobolev spaces.
Nagoya Mathematical Journal,
Vol. 186,
Issue. ,
p.
29.
Peng, Ru
and
Ouyang, Caiheng
2008.
Pointwise multipliers from Dirichlet type spaces Dτ to Qp spaces in the unit ball of Cn∗.
Journal of Mathematical Analysis and Applications,
Vol. 338,
Issue. 2,
p.
1448.
Arcozzi, N.
Rochberg, R.
and
Sawyer, E.
2008.
Carleson measures for the Drury–Arveson Hardy space and other Besov–Sobolev spaces on complex balls.
Advances in Mathematics,
Vol. 218,
Issue. 4,
p.
1107.
Tchoundja, Edgar
2008.
Carleson measures for Hardy–Sobolev spaces.
Complex Variables and Elliptic Equations,
Vol. 53,
Issue. 11,
p.
1033.
Tchoundja, Edgar
2008.
Carleson measures for the generalized Bergman spaces via a T(1)-type theorem.
Arkiv för Matematik,
Vol. 46,
Issue. 2,
p.
377.
Li, Songxiao
and
Shamoyan, Romi
2010.
On some estimates and Carleson type measure for multifunctional holomorphic spaces in the unit ball.
Bulletin des Sciences Mathématiques,
Vol. 134,
Issue. 2,
p.
144.
Cascante, Carme
Fàbrega, Joan
and
Ortega, Joaquín M.
2010.
On Weighted Toeplitz, Big Hankel Operators and Carleson Measures.
Integral Equations and Operator Theory,
Vol. 66,
Issue. 4,
p.
495.
Cao, GuangFu
and
He, Li
2014.
Hardy-Sobolev spaces and their multipliers.
Science China Mathematics,
Vol. 57,
Issue. 11,
p.
2361.
Cao, Guangfu
and
He, Li
2014.
Fredholmness of multipliers on Hardy–Sobolev spaces.
Journal of Mathematical Analysis and Applications,
Vol. 418,
Issue. 1,
p.
1.
Tupputi, Maria Rosaria
2015.
Weighted Inequalities in Some Potential Spaces on the Upper Half Space of ℝ n+1.
Potential Analysis,
Vol. 42,
Issue. 1,
p.
293.
Chalmoukis, Nikolaos
and
Hartz, Michael
2022.
Totally null sets and capacity in Dirichlet type spaces.
Journal of the London Mathematical Society,
Vol. 106,
Issue. 3,
p.
2030.




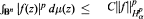 . for any ƒ ∈
. for any ƒ ∈ 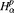 where
where 