Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T16:52:29.454Z Has data issue: false hasContentIssue false
  • English
  • Français

La Variante infinitésimale de la formule des traces de Jacquet—Rallis pour les groupesunitaires

Published online by Cambridge University Press:  20 November 2018

Michał Zydor
Michał Zydor*
Affiliation:
Université Paris Diderot, Institut de Mathématiques de Jussieu-Paris Rive Gauche, UMR7586, Bâtiment Sophie Germain, Case 7012, 75205 PARIS Cedex 13, France courriel: michalz@weizmann.ac.il
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Nous établissons une variante infinitésimale de la formule des traces de Jacquet-Rallis pour les groupes unitaires. Notre formule s’obtient par intégration d'un noyau tronqué á la Arthur. Elle posséde un côté géométrique qui est une somme de distributions 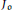${{J}_{\mathfrak{o}}}$ indexée par les classes d'éléments de l'algébre de Lie de 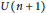$U\,\left( n\,+\,1 \right)$ stables par 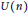$U\left( n \right)$-conjugaison ainsi qu'un “côté spectral” formé des transformées de Fourier des distributions précédentes. On démontre que les distributions 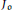${{J}_{\mathfrak{o}}}$ sont invariantes et ne dépendent que du choix de la mesure de Haar sur 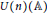$U\left( n \right)\left( \mathbb{A} \right)$. Pour des classes $\mathfrak{o}$ semi-simples réguliéres, 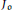${{J}_{\mathfrak{o}}}$ est une intégrale orbitale relative de Jacquet-Rallis. Pour les classes $\mathfrak{o}$ dites relativement semi-simples régulières, on exprime 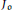${{J}_{\mathfrak{o}}}$ en terme des intégrales orbitales relatives régularisées á l'aide des fonctions zêta.

Keywords

11F7011F72formule des traces relative
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 6 , 01 December 2016 , pp. 1382 - 1435
Copyright
Copyright © Canadian Mathematical Society 2016

References

Références

[1] Arthur, J., The trace formula in invariant form. Ann. of Math. (2) 114(1981), no. 1,1–74. http://dx.doi.Org/10.2307/1971376 Google Scholar
[2] Arthur, J., A trace formula for reductive groups. I. Terms associated to classes in G(Q). Duke Math. J. 45(1978), no. 4, 911–952. http://dx.doi.org/10.1215/S0012-7094-78-04542-8 Google Scholar
[3] Arthur, J., A local trace formula. Inst. Hautes Études Sci. Publ. Math. (1991), no. 73, 5–96.Google Scholar
[4] Chaudouard, P-H., La formule des traces pour les algèbres de Lie. Math. Ann. 322(2002), no. 2, 347–382.http://dx.doi.Org/10.1OO7/sOO2O8O100274 Google Scholar
[5] Chaudouard, P-H., Intégrales orbitales pondérées sur les algèbres de Lie : le cas p-adique. Canad. J. Math. 54(2002), no. 2, 263–302. http://dx.doi.Org/10.4153/CJM-2OO2-OO9-6 Google Scholar
[6] Gan, W. T., Gross, B. H., and Prasad, D., Symplectic local root numbers, central critical L values, and restriction problems in the representation theory of classical groups. Astérisque (2012), no. 346, 1–109.Google Scholar
[7] Harris, R.N., The refined Gross-Prasad conjecture for unitary groups. Int. Math. Res. Not. IMRN (2014), no. 2, 303–389.Google Scholar
[8] Ichino, A. and Ikeda, T., On the periods of automorphic forms on special orthogonal groups and the Gross-Prasad conjecture. Geom. Funct. Anal. 19(2010), no. 5,1378–1425. http://dx.doi.Org/10.1007/s00039-009-0040-4 Google Scholar
[9] Ichino, A. and Yamana, S., Periods of automorphic form : the case o/(Un+1 x Un, Un). Prépublication. (2015).Google Scholar
[10] Jacquet, H., Lapid, E., and Rogawski, J., Periods of automorphic forms. J. Amer. Math. Soc. 12(1999), no. 1,173–240. http://dx.doi.org/10.1090/S0894-0347-99-00279-9 Google Scholar
[11] Jacquet, H. and Rallis, S., On the Gross-Prasad conjecture for unitary groups. In : On certain L-functions, Clay Math. Proa, Amer. Math. Soc, 2011, pp. 205–265.Google Scholar
[12] Knus, M. A., Merkurjev, A., Rost, M., and Tignol, J.-P., The book of involutions. American Mathematical Society Colloquium Publications 44, With a preface in French by J. Tits, American Mathematical Society, Providence, RI, 1998.Google Scholar
[13] Levy, J., A truncated integral of the Poisson summation formula. Can. J. Math. 53(2001), no. 1, 122–160.Preprint arXivhttp://dx.doi.Org/10.4153/CJM-2OO1-006-1 Google Scholar
[14] Labesse, J.-P. and Waldspurger, J.-L., La formule des traces tordue d'après le Friday Morning Seminar. CRM Monograph Series 31. American Mathematical Society, Providence, RI, 2013.Google Scholar
[15] Rallis, S. and Schiffmann, G., Multiplicity one conjectures. arxiv:O7O5.21268(2OO8) Google Scholar
[16] Varadarajan, V. S., Harmonic analysis on real reductive groups. Lecture Notes in Mathematics 576 ,Springer-Verlag, Berlin-New York, 1977.Google Scholar
[17] Waldspurger, J.-L., Le lemme fondamental implique le transfert. Compositio Math. (1997), no. 2, 153–236. http://dx.doi.Org/10.1023/A:1000103112268 Google Scholar
[18] Zhang, W., Fourier transform and the global Gan-Gross-Prasad conjecture for unitary groups. Google Scholar
[19] Zhang, W., Automorphic period and the central value of Rankin-Selberg L-function. J. Amer. Math. Soc. 27(2014), no. 2, 541–612. http://dx.doi.Org/10.1090/S0894-0347-2014-00784-0 Google Scholar
[20] Zydor, M., La variante infinitésimale de la formule des traces de Jacquet-Rallis pour les groupes linéaires. arxiv:1310.1650(2015) Google Scholar
[21] Zydor, M., Les formules des traces relatives de Jacquet-Rallis grossières. arxiv:1510.04301(2015) Google Scholar