Article contents
Images of multilinear graded polynomials on upper triangular matrix algebras
Published online by Cambridge University Press: 19 September 2022
Abstract
In this paper, we study the images of multilinear graded polynomials on the graded algebra of upper triangular matrices 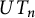 $UT_n$. For positive integers
$UT_n$. For positive integers 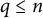 $q\leq n$, we classify these images on
$q\leq n$, we classify these images on 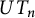 $UT_{n}$ endowed with a particular elementary
$UT_{n}$ endowed with a particular elementary 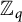 ${\mathbb {Z}}_{q}$-grading. As a consequence, we obtain the images of multilinear graded polynomials on
${\mathbb {Z}}_{q}$-grading. As a consequence, we obtain the images of multilinear graded polynomials on 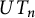 $UT_{n}$ with the natural
$UT_{n}$ with the natural 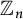 ${\mathbb {Z}}_{n}$-grading. We apply this classification in order to give a new condition for a multilinear polynomial in terms of graded identities so that to obtain the traceless matrices in its image on the full matrix algebra. We also describe the images of multilinear polynomials on the graded algebras
${\mathbb {Z}}_{n}$-grading. We apply this classification in order to give a new condition for a multilinear polynomial in terms of graded identities so that to obtain the traceless matrices in its image on the full matrix algebra. We also describe the images of multilinear polynomials on the graded algebras 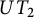 $UT_{2}$ and
$UT_{2}$ and 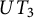 $UT_{3}$, for arbitrary gradings. We finish the paper by proving a similar result for the graded Jordan algebra
$UT_{3}$, for arbitrary gradings. We finish the paper by proving a similar result for the graded Jordan algebra 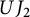 $UJ_{2}$, and also for
$UJ_{2}$, and also for 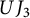 $UJ_{3}$ endowed with the natural elementary
$UJ_{3}$ endowed with the natural elementary 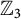 ${\mathbb {Z}}_{3}$-grading.
${\mathbb {Z}}_{3}$-grading.
Keywords
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
P. Fagundes was supported by São Paulo Research Foundation (FAPESP), Grant No. 2019/16994-1. P. Koshlukov was partially supported by São Paulo Research Foundation (FAPESP), Grant No. 2018/23690-6 and by CNPq Grant No. 302238/2019-0.
References
- 4
- Cited by



