Article contents
Classification of Regular ParametrizedOne-relation Operads
Published online by Cambridge University Press: 20 November 2018
Abstract
Jean-Louis Loday introduced a class of symmetric operads generated by one bilinear operation subject to one relation making each left-normed product of three elements equal to a linear combination of right-normed products: 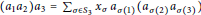 $({{a}_{1}}{{a}_{2}}){{a}_{3}}\,=\,\sum{{{_{\sigma }}_{\in {{s}_{3}}}}\,}{{x}_{\sigma }}\,{{a}_{\sigma \,(1)}}({{a}_{\sigma (2)\,}}{{a}_{\sigma (3)}})$. Such an operad is called a parametrized one-relation operad. For a particular choice of parameters
$({{a}_{1}}{{a}_{2}}){{a}_{3}}\,=\,\sum{{{_{\sigma }}_{\in {{s}_{3}}}}\,}{{x}_{\sigma }}\,{{a}_{\sigma \,(1)}}({{a}_{\sigma (2)\,}}{{a}_{\sigma (3)}})$. Such an operad is called a parametrized one-relation operad. For a particular choice of parameters 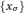 $\{{{x}_{\sigma }}\}$, this operad is said to be regular if each of its components is the regular representation of the symmetric group; equivalently, the corresponding free algebra on a vector space
$\{{{x}_{\sigma }}\}$, this operad is said to be regular if each of its components is the regular representation of the symmetric group; equivalently, the corresponding free algebra on a vector space 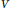 $V$ is, as a graded vector space, isomorphic to the tensor algebra of
$V$ is, as a graded vector space, isomorphic to the tensor algebra of 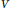 $V$. We classify, over an algebraically closed field of characteristic zero, all regular parametrized one-relation operads. In fact, we prove that each such operad is isomorphic to one of the following five operads: the left-nilpotent operad defined by the relation
$V$. We classify, over an algebraically closed field of characteristic zero, all regular parametrized one-relation operads. In fact, we prove that each such operad is isomorphic to one of the following five operads: the left-nilpotent operad defined by the relation 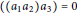 $(({{a}_{1}}{{a}_{2}}){{a}_{3}})\,=\,0$, the associative operad, the Leibniz operad, the dual Leibniz (Zinbiel) operad, and the Poisson operad. Our computational methods combine linear algebra over polynomial rings, representation theory of the symmetric group, and Gröbner bases for determinantal ideals and their radicals.
$(({{a}_{1}}{{a}_{2}}){{a}_{3}})\,=\,0$, the associative operad, the Leibniz operad, the dual Leibniz (Zinbiel) operad, and the Poisson operad. Our computational methods combine linear algebra over polynomial rings, representation theory of the symmetric group, and Gröbner bases for determinantal ideals and their radicals.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
- 7
- Cited by


