Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
de Rosa, Liliana
and
Segovia, Carlos
1997.
One-sided Littlewood-Paley theory.
Journal of Fourier Analysis and Applications,
Vol. 3,
Issue. S1,
p.
933.
Riveros, M. S.
and
de la Torre, A.
2000.
Norm inequalities relating one-sided singular integrals and the one-sided maximal function.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 69,
Issue. 3,
p.
403.
Riveros, M. S.
and
Torre, A. de la
2001.
On the Best Ranges for Ap+ and RHr+.
Czechoslovak Mathematical Journal,
Vol. 51,
Issue. 2,
p.
285.
Lorente, M.
and
Riveros, M. S.
2005.
Two weight norm inequalities for communtators of one-sided singular integrals and the one-sided discrete square function.
Journal of the Australian Mathematical Society,
Vol. 79,
Issue. 1,
p.
77.
Ombrosi, Sheldy
Segovia, Carlos
and
Testoni, Ricardo
2006.
An interpolation theorem between one-sided Hardy spaces.
Arkiv för Matematik,
Vol. 44,
Issue. 2,
p.
335.
Lorente, María
Riveros, María Silvina
and
de la Torre, Alberto
2007.
On the Coifman type inequality for the oscillation of one-sided averages.
Journal of Mathematical Analysis and Applications,
Vol. 336,
Issue. 1,
p.
577.
Lorente, María
Martell, José María
Riveros, María Silvina
and
de la Torre, Alberto
2008.
Generalized Hörmander's conditions, commutators and weights.
Journal of Mathematical Analysis and Applications,
Vol. 342,
Issue. 2,
p.
1399.
Lorente, María
and
de la Torre, Alberto
2008.
Weighted and Ergodic Theorems for Series of Differences of Convolutions.
Journal of Fourier Analysis and Applications,
Vol. 14,
Issue. 1,
p.
39.
Martín-Reyes, Francisco Javier
Ortega, Pedro
and
de Torre, Alberto la
2010.
Recent Developments in Real and Harmonic Analysis.
p.
97.
Salvador, Pedro Ortega
and
Torreblanca, Consuelo Ramírez
2011.
Weighted inequalities for the one‐sided geometric maximal operators.
Mathematische Nachrichten,
Vol. 284,
Issue. 11-12,
p.
1515.
Shi, Shaoguang
Fu, Zunwei
and
Lu, Shanzhen
2011.
Weighted estimates for commutators of one-sided oscillatory integral operators.
Frontiers of Mathematics in China,
Vol. 6,
Issue. 3,
p.
507.
Berkovits, Lauri
2011.
Parabolic Muckenhoupt weights in the Euclidean space.
Journal of Mathematical Analysis and Applications,
Vol. 379,
Issue. 2,
p.
524.
Fu, Zunwei
Lu, Shanzhen
Pan, Yibiao
and
Shi, Shaoguang
2014.
Boundedness of One-Sided Oscillatory Integral Operators on Weighted Lebesgue Spaces.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
Zhang, Xiao Jin
and
Hou, Xian Ming
2014.
Lipschitz Estimates for One-Sided Cohen’s Commutators on Weighted One-Sided Triebel-Lizorkin Spaces.
Journal of Function Spaces,
Vol. 2014,
Issue. ,
p.
1.
Martín-Reyes, Francisco J.
and
de la Torre, Alberto
2015.
Sharp weighted bounds for one-sided maximal operators.
Collectanea Mathematica,
Vol. 66,
Issue. 2,
p.
161.
Kinnunen, Juha
and
Saari, Olli
2016.
On weights satisfying parabolic Muckenhoupt conditions.
Nonlinear Analysis,
Vol. 131,
Issue. ,
p.
289.
Kinnunen, Juha
and
Saari, Olli
2016.
Parabolic weighted norm inequalities and partial differential equations.
Analysis & PDE,
Vol. 9,
Issue. 7,
p.
1711.
Bernardis, Ana
Martín-Reyes, Francisco J.
Stinga, Pablo Raúl
and
Torrea, José L.
2016.
Maximum principles, extension problem and inversion for nonlocal one-sided equations.
Journal of Differential Equations,
Vol. 260,
Issue. 7,
p.
6333.
Shi, Shaoguang
and
Zhang, Lei
2016.
Norm inequalities for higher-order commutators of one-sided oscillatory singular integrals.
Journal of Inequalities and Applications,
Vol. 2016,
Issue. 1,
Hagelstein, Paul
Parissis, Ioannis
and
Saari, Olli
2018.
Sharp inequalities for one-sided Muckenhoupt weights.
Collectanea Mathematica,
Vol. 69,
Issue. 1,
p.
151.
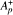
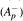 . In this paper we introduce a new condition
. In this paper we introduce a new condition 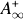 which is analogous to A∞. We show several characterizations of
which is analogous to A∞. We show several characterizations of 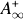 . For example, we prove that the class of
. For example, we prove that the class of 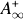 weights is the union of
weights is the union of 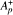 classes. We also give a new characterization of
classes. We also give a new characterization of 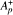 weights. Finally, as an application of
weights. Finally, as an application of 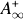 condition, we characterize the weights for one-sided fractional integrals and one-sided fractional maximal operators.
condition, we characterize the weights for one-sided fractional integrals and one-sided fractional maximal operators.

