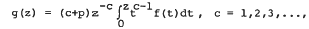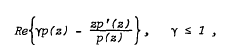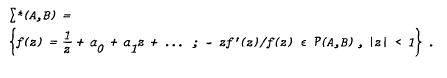Research Article
Metric spaces which cannot be isometrically embedded in Hilbert space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-167
-
- Article
-
- You have access
- Export citation
On second derivative estimates for equations of Monge-Ampère type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-334
-
- Article
-
- You have access
- Export citation
Fixed point theorems by altering distances between the points
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-9
-
- Article
-
- You have access
- Export citation
Does the Frobenius endomorphism always generate a direct summand in the endomorphism monoids of fields of prime characteristic?
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 335-356
-
- Article
-
- You have access
- Export citation
A note on the central limit theorem for geodesic random walks
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-173
-
- Article
-
- You have access
- Export citation
On the structure of polynomially normal operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 11-18
-
- Article
-
- You have access
- Export citation
Efficiency of a university timetable. An application of entropy of choice.
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 19-26
-
- Article
-
- You have access
- Export citation
On orthogonally decomposable ordered Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-380
-
- Article
-
- You have access
- Export citation
A remark on products of locally soluble groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 175-177
-
- Article
-
- You have access
- Export citation
An effective seven cube theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 381-385
-
- Article
-
- You have access
- Export citation
Two-sided localization in semiprime FBN rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 179-191
-
- Article
-
- You have access
- Export citation
On a C–plane of order 25
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 27-36
-
- Article
-
- You have access
- Export citation
On p–valent starlike functions with reference to the Bernardi integral operator
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 37-43
-
- Article
-
- You have access
- Export citation
An oscillation theorem for sublinear elliptic differential inequalities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 387-394
-
- Article
-
- You have access
- Export citation
Generalized convexity in nondifferentiable programming
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 193-218
-
- Article
-
- You have access
- Export citation
Forms of low degree in finite fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 45-58
-
- Article
-
- You have access
- Export citation
Elliptic differential operators and diffusion processes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 219-237
-
- Article
-
- You have access
- Export citation
Meromorphic starlike univalent functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 395-410
-
- Article
-
- You have access
- Export citation
Isometries and certain dynamical systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 239-246
-
- Article
-
- You have access
- Export citation
A class of translation planes of square order
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 59-66
-
- Article
-
- You have access
- Export citation



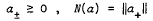 and
and 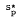 (A, B) denote the class of certain p-valent starlike functions. Recently G. Lakshma Reddy and K.S. Padmanabhan [Bull. Austral. Math. Soc. 25 (1982), 387–396] have shown that the function g defined by
(A, B) denote the class of certain p-valent starlike functions. Recently G. Lakshma Reddy and K.S. Padmanabhan [Bull. Austral. Math. Soc. 25 (1982), 387–396] have shown that the function g defined by