Research Article
CHARACTERIZATIONS OF HYPERSURFACES OF TYPE A2 IN A COMPLEX PROJECTIVE SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 1-8
-
- Article
-
- You have access
- Export citation
AN ALGORITHM FOR FINDING ALL ZEROS OF VECTOR FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 353-363
-
- Article
-
- You have access
- Export citation
WARPED PRODUCT SEMI-SLANT SUBMANIFOLDS IN LOCALLY RIEMANNIAN PRODUCT MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 177-186
-
- Article
-
- You have access
- Export citation
RIGIDITY OF GRAPH PRODUCTS OF ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 187-196
-
- Article
-
- You have access
- Export citation
OUTER AUTOMORPHISM GROUPS OF CERTAIN TREE PRODUCTS OF ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 9-20
-
- Article
-
- You have access
- Export citation
A NEW MEAN WITH INEQUALITIES
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 365-371
-
- Article
-
- You have access
- Export citation
LOCAL RADIAL BASIS FUNCTION APPROXIMATION ON THE SPHERE
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 197-224
-
- Article
-
- You have access
- Export citation
A MODEL OF UNIVERSAL TEICHMÜLLER SPACE AND ITS APPLICATION
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 21-30
-
- Article
-
- You have access
- Export citation
CONTACT METRIC (κ,μ)-SPACES AS BI-LEGENDRIAN MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 373-386
-
- Article
-
- You have access
- Export citation
HIGHER EPISTASIS IN GENETIC ALGORITHMS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 225-243
-
- Article
-
- You have access
- Export citation
COMMUTATIVITY DEGREES OF WREATH PRODUCTS OF FINITE ABELIAN GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 31-36
-
- Article
-
- You have access
- Export citation
UNIFORM APPROXIMATION BY POLYNOMIAL, RATIONAL AND ANALYTIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 387-399
-
- Article
-
- You have access
- Export citation
ON THE FUNDAMENTAL REGIONS OF A FIXED POINT FREE CONSERVATIVE HÉNON MAP
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 37-48
-
- Article
-
- You have access
- Export citation
INEQUALITIES FOR SUPERADDITIVE FUNCTIONALS WITH APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 401-411
-
- Article
-
- You have access
- Export citation
MULTIDIMENSIONAL HARDY-TYPE INEQUALITIES VIA CONVEXITY
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 245-260
-
- Article
-
- You have access
- Export citation
A NOTE ON THE UNCLOUDING THE SKY OF NEGATIVELY CURVED MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2008, pp. 413-424
-
- Article
-
- You have access
- Export citation
SCHUR MULTIPLICATIVE MAPS ON MATRICES
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 49-72
-
- Article
-
- You have access
- Export citation
AUTOMORPHISMS OF METABELIAN PRIME POWER ORDER GROUPS OF MAXIMAL CLASS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 261-276
-
- Article
-
- You have access
- Export citation
APPROXIMATING THE STIELTJES INTEGRAL FOR (φ,Φ)-LIPSCHITZIAN INTEGRATORS
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2008, pp. 73-90
-
- Article
-
- You have access
- Export citation
NEIGHBOURHOODS OF INDEPENDENT SETS FOR (a,b,k)-CRITICAL GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2008, pp. 277-283
-
- Article
-
- You have access
- Export citation



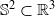 . More precisely, we consider radial basis function interpolation based on data on a (global or local) point set
. More precisely, we consider radial basis function interpolation based on data on a (global or local) point set 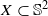 for functions in the Sobolev space
for functions in the Sobolev space 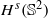 with norm
with norm 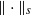 , where
, where 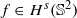 satisfies
satisfies 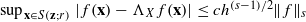 , where
, where 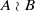 of finite Abelian groups
of finite Abelian groups 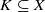 . Let
. Let 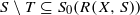 and
and 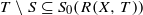 ;
;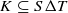 ;
;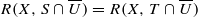 for every open set
for every open set 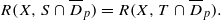
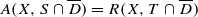 for every closed disk
for every closed disk 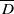 in ℂ ;
in ℂ ;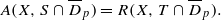
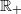 for some positive constants
for some positive constants 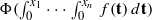 instead of
instead of 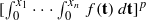 , while the corresponding right-hand sides remain as in the classical Hardy’s inequality and have explicit constants in front of integrals. We also prove the related dual inequalities. The relations obtained are new even for the one-dimensional case and they unify and extend several inequalities of Hardy type known in the literature.
, while the corresponding right-hand sides remain as in the classical Hardy’s inequality and have explicit constants in front of integrals. We also prove the related dual inequalities. The relations obtained are new even for the one-dimensional case and they unify and extend several inequalities of Hardy type known in the literature.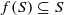 for different subsets
for different subsets