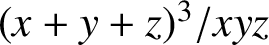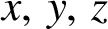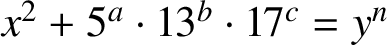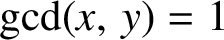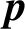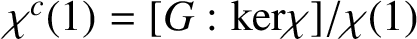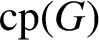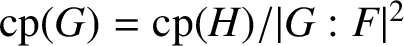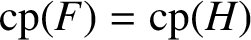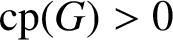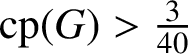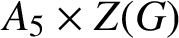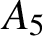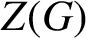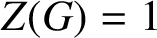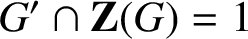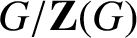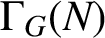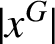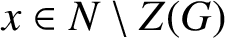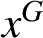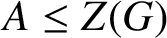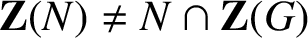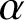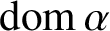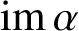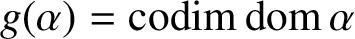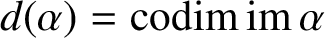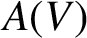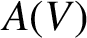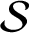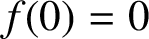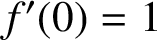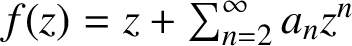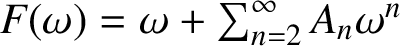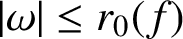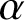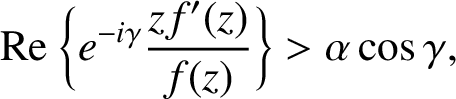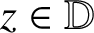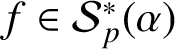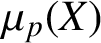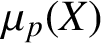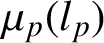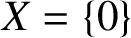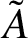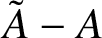Research Article
ENUMERATING NECKLACES WITH TRANSITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2021, pp. 1-11
-
- Article
- Export citation
ON A PROBLEM OF RICHARD GUY
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2021, pp. 12-18
-
- Article
- Export citation
SOLUTIONS TO A LEBESGUE–NAGELL EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2021, pp. 19-30
-
- Article
- Export citation
ELLIPTIC CURVES AND
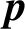 $\boldsymbol {p}$
-ADIC ELLIPTIC TRANSCENDENCE
$\boldsymbol {p}$
-ADIC ELLIPTIC TRANSCENDENCE
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2021, pp. 31-36
-
- Article
- Export citation
DETERMINANTS AND PERMANENTS OF POWER MATRICES
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2021, pp. 37-45
-
- Article
- Export citation
HANKEL DETERMINANTS OF FACTORIAL FRACTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2021, pp. 46-57
-
- Article
- Export citation
STRUCTURED SINGULAR VALUES OF SOME GENERALISED STOCHASTIC MATRICES
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2021, pp. 58-67
-
- Article
- Export citation
NONDIVISIBILITY AMONG IRREDUCIBLE CHARACTER CO-DEGREES
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2021, pp. 68-74
-
- Article
- Export citation
GROUPS WITH MANY PRONORMAL SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2021, pp. 75-86
-
- Article
-
- You have access
- Open access
- Export citation
COMMUTING PROBABILITY OF COMPACT GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 24 June 2021, pp. 87-91
-
- Article
- Export citation
EXTENDING RESULTS OF MORGAN AND PARKER ABOUT COMMUTING GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2021, pp. 92-100
-
- Article
- Export citation
ON THE REGULAR GRAPH RELATED TO THE G-CONJUGACY CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2021, pp. 101-105
-
- Article
- Export citation
INJECTIVE LINEAR TRANSFORMATIONS WITH EQUAL GAP AND DEFECT
- Part of:
-
- Published online by Cambridge University Press:
- 18 May 2021, pp. 106-116
-
- Article
- Export citation
A NOTE ON SPIRALLIKE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 25 March 2021, pp. 117-123
-
- Article
- Export citation
REVISITING THE RECTANGULAR CONSTANT IN BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2021, pp. 124-133
-
- Article
-
- You have access
- Open access
- Export citation
THE BOCHNER–SCHOENBERG-EBERLEIN PROPERTY OF EXTENSIONS OF BANACH ALGEBRAS AND BANACH MODULES
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2021, pp. 134-145
-
- Article
- Export citation
AN UNBOUNDED OPERATOR WITH SPECTRUM IN A STRIP AND MATRIX DIFFERENTIAL OPERATORS
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2021, pp. 146-153
-
- Article
-
- You have access
- Open access
- Export citation
NOTES ON ORTHOGONAL-COMPLETE METRIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2021, pp. 154-160
-
- Article
- Export citation
ON THE CONNECTEDNESS OF THE CHABAUTY SPACE OF A LOCALLY COMPACT PRONILPOTENT GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2021, pp. 161-170
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
STATISTICAL STABILITY FOR DETERMINISTIC AND RANDOM DYNAMICAL SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 171-172
-
- Article
-
- You have access
- HTML
- Export citation