Article contents
A UNIQUE REPRESENTATION BI-BASIS FOR THE INTEGERS. II
Published online by Cambridge University Press: 08 January 2016
Abstract
For 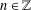 $n\in \mathbb{Z}$ and
$n\in \mathbb{Z}$ and  $A\subseteq \mathbb{Z}$, define
$A\subseteq \mathbb{Z}$, define 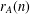 $r_{A}(n)$ and
$r_{A}(n)$ and 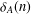 ${\it\delta}_{A}(n)$ by
${\it\delta}_{A}(n)$ by  $r_{A}(n)=\#\{(a_{1},a_{2})\in A^{2}:n=a_{1}+a_{2},a_{1}\leq a_{2}\}$ and
$r_{A}(n)=\#\{(a_{1},a_{2})\in A^{2}:n=a_{1}+a_{2},a_{1}\leq a_{2}\}$ and 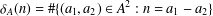 ${\it\delta}_{A}(n)=\#\{(a_{1},a_{2})\in A^{2}:n=a_{1}-a_{2}\}$. We call
${\it\delta}_{A}(n)=\#\{(a_{1},a_{2})\in A^{2}:n=a_{1}-a_{2}\}$. We call 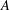 $A$ a unique representation bi-basis if
$A$ a unique representation bi-basis if 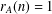 $r_{A}(n)=1$ for all
$r_{A}(n)=1$ for all 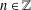 $n\in \mathbb{Z}$ and
$n\in \mathbb{Z}$ and 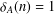 ${\it\delta}_{A}(n)=1$ for all
${\it\delta}_{A}(n)=1$ for all 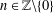 $n\in \mathbb{Z}\setminus \{0\}$. In this paper, we prove that there exists a unique representation bi-basis
$n\in \mathbb{Z}\setminus \{0\}$. In this paper, we prove that there exists a unique representation bi-basis 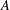 $A$ such that
$A$ such that 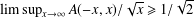 $\limsup _{x\rightarrow \infty }A(-x,x)/\sqrt{x}\geq 1/\sqrt{2}$.
$\limsup _{x\rightarrow \infty }A(-x,x)/\sqrt{x}\geq 1/\sqrt{2}$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by




