Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-18T04:26:59.145Z Has data issue: false hasContentIssue false
  • English
  • Français

Topologies on locally compact groups

Published online by Cambridge University Press:  17 April 2009

Joan Cleary  and
Sidney A. Morris
Joan Cleary
Affiliation:
Department of Mathematics, La Trobe University, Bundoora, Vic. 3803, Australia
Sidney A. Morris
Affiliation:
Department of Mathematics, Statistics and Computing Science, The University of New England, Armidale, N.S.W. 2351, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using the Iwasawa structure theorem for connected locally compact Hausdorff groups we show that every locally compact Hausdorff group G is homeomorphic to Rn × K × D, where n is a non-negative integer, K is a compact group and D is a discrete group. This makes recent results on cardinal numbers associated with the topology of locally compact groups more transparent. For abelian G, we note that the dual group, Ĝ, is homeomorphic to 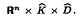This leads us to the relationship card G = ω0(Ĝ) + 2ω0(G), where ω (respectively, ω0) denotes the weight (respectively local weight) of the topological group. From this classical results such as card G = 2 card Ĝ for compact Hausdorff abelian groups, and ω(G) = ω(Ĝ) for general locally compact Hausdorff abelian groups are easily derived.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 38 , Issue 1 , August 1988 , pp. 105 - 111
Copyright
Copyright © Australian Mathematical Society 1988

References

[1]Bagley, R.W. and Peyrovian, M.R., ‘A note on compact subgroups of topological groups’, Bull. Austral. Math. Soc. 33 (1986), 273–278.CrossRefGoogle Scholar
[2]Cleary, Joan and Morris, Sidney A., ‘Trinity … A tale of three cardinals’, Proc. Centre Mathematical Analysis 14 (1986), 117–127.Google Scholar
[3]Comfort, W.W., ‘Topological Groups’, in Handbook of set-theoretic topology, Kunen, K. and Vaughan, J.E. eds., pp. 1143–1264 (North-Holland, Amsterdam, 1984).CrossRefGoogle Scholar
[4]Hewitt, Edwin and Ross, Kenneth A., Abstract Harmoic Analysis (Springer-Verlag, Berlin, 1963).Google Scholar
[5]Hewitt, Edwin and Ross, Kenneth A., Abstract Harmonic Analysis II (Springer-Verlag, Berlin, 1970).Google Scholar
[6]Hochschild, G., The Structure of Lie Groups (Holden-Day Inc., San Francisco, 1965).Google Scholar
[7]Morris, Sidney A., Pontryagin Duality and the Structure of Locally Compact Abelian Groups (Cambridge University Press, Cambridge, 1977).CrossRefGoogle Scholar
[8]Mostert, Paul S., ‘Sections in principle fibre spaces’, Duke Math. J. 23 (1956), 57–71.CrossRefGoogle Scholar