Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-23T20:29:58.246Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SUBGROUP COMMUTATIVITY DEGREE OF FINITE 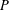$P$-GROUPS

Part of: Representation theory of groups Probabilistic methods in group theory Special aspects of infinite or finite groups

Published online by Cambridge University Press:  08 July 2015

MARIUS TĂRNĂUCEANU
MARIUS TĂRNĂUCEANU*
Affiliation:
Faculty of Mathematics, ‘Al. I. Cuza’ University, Iaşi, Romania email tarnauc@uaic.ro
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The subgroup commutativity degree of a group 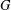$G$ is the probability that two subgroups of 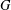$G$ commute, or equivalently that the product of two subgroups is again a subgroup. For the dihedral, quasi-dihedral and generalised quaternion groups (all of 2-power cardinality), the subgroup commutativity degree tends to 0 as the size of the group tends to infinity. This also holds for the family of projective special linear groups over fields of even characteristic and for the family of the simple Suzuki groups. In this short note, we show that the family of finite 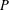$P$-groups also has this property.

Keywords

subgroup commutativity degreessubgroup latticesfinite P-groups

MSC classification

Primary: 20D60: Arithmetic and combinatorial problems 20P05: Probabilistic methods in group theory
Secondary: 20D30: Series and lattices of subgroups 20F16: Solvable groups, supersolvable groups 20F18: Nilpotent groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 1 , February 2016 , pp. 37 - 41
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Aivazidis, S., ‘The subgroup permutability degree of projective special linear groups over fields of even characteristic’, J. Group Theory 16 (2013), 383–396.CrossRefGoogle Scholar
Aivazidis, S., ‘On the subgroup permutability degree of the simple Suzuki groups’, Monatsh. Math. 176 (2015), 335–358.CrossRefGoogle Scholar
Schmidt, R., Subgroup Lattices of Groups, de Gruyter Expositions in Mathematics, 14 (de Gruyter, Berlin, 1994).CrossRefGoogle Scholar
Suzuki, M., Group Theory, I, II (Springer, Berlin, 1982, 1986).Google Scholar
Tărnăuceanu, M., ‘A new method of proving some classical theorems of abelian groups’, Southeast Asian Bull. Math. 31 (2007), 1191–1203.Google Scholar
Tărnăuceanu, M., ‘Subgroup commutativity degrees of finite groups’, J. Algebra 321 (2009), 2508–2520.CrossRefGoogle Scholar
Tărnăuceanu, M., ‘An arithmetic method of counting the subgroups of a finite abelian group’, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 53(101) (2010), 373–386.Google Scholar
Tărnăuceanu, M., ‘Addendum to “Subgroup commutativity degrees of finite groups”’, J. Algebra 337 (2011), 363–368.CrossRefGoogle Scholar