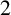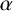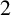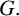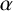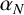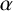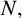1 Introduction
Throughout this paper, G will denote a finite group and it will be implicitly assumed that all projective representations affording projective characters are defined over the field of complex numbers
![]() $\mathbb {C}.$
$\mathbb {C}.$
Definition 1.1. A
![]() $2$
-cocycle of G over
$2$
-cocycle of G over
![]() $\mathbb {C}$
is a function
$\mathbb {C}$
is a function
![]() $\alpha : G\times G\rightarrow \mathbb {C}^*$
such that
$\alpha : G\times G\rightarrow \mathbb {C}^*$
such that
![]() $\alpha (1, 1) = 1$
and
$\alpha (1, 1) = 1$
and
![]() $\alpha (x, y)\alpha (xy, z) = \alpha (x, yz)\alpha (y, z)$
for all x, y,
$\alpha (x, y)\alpha (xy, z) = \alpha (x, yz)\alpha (y, z)$
for all x, y,
![]() $z\in G.$
$z\in G.$
The set of all such
![]() $2$
-cocycles of G form a group
$2$
-cocycles of G form a group
![]() $Z^2(G, \mathbb {C}^*)$
under multiplication. Let
$Z^2(G, \mathbb {C}^*)$
under multiplication. Let
![]() $\delta : G\rightarrow \mathbb {C}^*$
be any function with
$\delta : G\rightarrow \mathbb {C}^*$
be any function with
![]() $\delta (1) = 1.$
Then
$\delta (1) = 1.$
Then
![]() $t(\delta )(x, y) = \delta (x)\delta (y)/\delta (xy)$
for all
$t(\delta )(x, y) = \delta (x)\delta (y)/\delta (xy)$
for all
![]() $x, y\in G$
is a
$x, y\in G$
is a
![]() $2$
-cocycle of G, which is called a coboundary. Two
$2$
-cocycle of G, which is called a coboundary. Two
![]() $2$
-cocycles
$2$
-cocycles
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are cohomologous if there exists a coboundary
$\beta $
are cohomologous if there exists a coboundary
![]() $t(\delta )$
such that
$t(\delta )$
such that
![]() $\beta = t(\delta )\alpha .$
This defines an equivalence relation on
$\beta = t(\delta )\alpha .$
This defines an equivalence relation on
![]() $Z^2(G, \mathbb {C}^*)$
and the cohomology classes
$Z^2(G, \mathbb {C}^*)$
and the cohomology classes
![]() $[\alpha ]$
form a finite abelian group, called the Schur multiplier
$[\alpha ]$
form a finite abelian group, called the Schur multiplier
![]() $M(G).$
$M(G).$
Definition 1.2. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G.
$2$
-cocycle of G.
-
(a) Define
 $f_{\alpha }: G\times G\rightarrow \mathbb {C}^*$
by
$f_{\alpha }: G\times G\rightarrow \mathbb {C}^*$
by  $$ \begin{align*}f_{\alpha}(g, x) = \frac{\alpha(g, x)\alpha(gx, g^{-1})}{\alpha(g, g^{-1})}.\end{align*} $$
$$ \begin{align*}f_{\alpha}(g, x) = \frac{\alpha(g, x)\alpha(gx, g^{-1})}{\alpha(g, g^{-1})}.\end{align*} $$
-
(b) For each
 $x\in G$
, define
$x\in G$
, define
 $\alpha _x: C_G(x)\rightarrow \mathbb {C}^*$
by
$\alpha _x: C_G(x)\rightarrow \mathbb {C}^*$
by
 $\alpha _x(g) = \alpha (g, x)/\alpha (x, g).$
$\alpha _x(g) = \alpha (g, x)/\alpha (x, g).$
These two functions arise naturally in the twisted group algebra
![]() $(\mathbb {C}(G))_{\alpha }$
in which
$(\mathbb {C}(G))_{\alpha }$
in which
![]() $\bar {x}\bar {y} = \alpha (x, y)\overline {xy}$
for all
$\bar {x}\bar {y} = \alpha (x, y)\overline {xy}$
for all
![]() $x, y\in G$
(see [Reference Karpilovsky4, page 66]). Here,
$x, y\in G$
(see [Reference Karpilovsky4, page 66]). Here,
![]() $\bar {g}\bar {x}\bar {g}^{-1} = f_{\alpha }(g, x)\overline {gxg^{-1}}$
for
$\bar {g}\bar {x}\bar {g}^{-1} = f_{\alpha }(g, x)\overline {gxg^{-1}}$
for
![]() $g, x\in G$
and
$g, x\in G$
and
![]() $\bar {g}\bar {x}\bar {g}^{-1} = \alpha _x(g)\bar {x}$
if
$\bar {g}\bar {x}\bar {g}^{-1} = \alpha _x(g)\bar {x}$
if
![]() $g\in C_G(x).$
Also, if
$g\in C_G(x).$
Also, if
![]() $\beta = t(\delta )\alpha $
, then
$\beta = t(\delta )\alpha $
, then
![]() $f_{\beta }(g, x) = (\delta (x)/\delta (gxg^{-1}))f_{\alpha }(g, x)$
for all
$f_{\beta }(g, x) = (\delta (x)/\delta (gxg^{-1}))f_{\alpha }(g, x)$
for all
![]() $g, x\in G$
and consequently
$g, x\in G$
and consequently
![]() $\alpha _x = \beta _x.$
$\alpha _x = \beta _x.$
Now
![]() $\alpha _x\in \operatorname {\mathrm {Lin}}(C_G(x))$
from [Reference Read6, Lemma 4.2], where
$\alpha _x\in \operatorname {\mathrm {Lin}}(C_G(x))$
from [Reference Read6, Lemma 4.2], where
![]() $\operatorname {\mathrm {Lin}}(C_G(x))$
is the group of linear characters of
$\operatorname {\mathrm {Lin}}(C_G(x))$
is the group of linear characters of
![]() $C_G(x).$
The kernel of
$C_G(x).$
The kernel of
![]() $\alpha _x$
is the absolute centraliser
$\alpha _x$
is the absolute centraliser
![]() $C_{\alpha }(x)$
of x with respect to
$C_{\alpha }(x)$
of x with respect to
![]() $\alpha $
and
$\alpha $
and
![]() $C_G(x)/C_{\alpha }(x)\cong \langle \alpha _x\rangle .$
$C_G(x)/C_{\alpha }(x)\cong \langle \alpha _x\rangle .$
Definition 1.3. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G. Then
$2$
-cocycle of G. Then
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular if
$\alpha $
-regular if
![]() $\alpha _x$
is the trivial character of
$\alpha _x$
is the trivial character of
![]() $C_G(x)$
(or equivalently
$C_G(x)$
(or equivalently
![]() $C_{\alpha }(x) = C_G(x)).$
$C_{\alpha }(x) = C_G(x)).$
First, every element of G is
![]() $\alpha $
-regular if
$\alpha $
-regular if
![]() $[\alpha ]$
is trivial. Second, setting
$[\alpha ]$
is trivial. Second, setting
![]() $y = 1$
and
$y = 1$
and
![]() $z = 1$
in Definition 1.1 yields
$z = 1$
in Definition 1.1 yields
![]() $\alpha (x, 1) = 1$
and similarly
$\alpha (x, 1) = 1$
and similarly
![]() $\alpha (1, x) = 1$
for all
$\alpha (1, x) = 1$
for all
![]() $x\in G,$
and hence
$x\in G,$
and hence
![]() $1$
is always
$1$
is always
![]() $\alpha $
-regular. Third, if
$\alpha $
-regular. Third, if
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular, then it is
$\alpha $
-regular, then it is
![]() $\alpha ^k$
-regular for any integer
$\alpha ^k$
-regular for any integer
![]() $k.$
Finally, if
$k.$
Finally, if
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular, then so too is any conjugate of x (see [Reference Karpilovsky4, Lemma 2.6.1]), so that one may refer to the
$\alpha $
-regular, then so too is any conjugate of x (see [Reference Karpilovsky4, Lemma 2.6.1]), so that one may refer to the
![]() $\alpha $
-regular conjugacy classes of
$\alpha $
-regular conjugacy classes of
![]() $G.$
$G.$
Now let
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
denote the set of all irreducible
$\operatorname {\mathrm {Proj}}(G, \alpha )$
denote the set of all irreducible
![]() $\alpha $
-characters of G (see [Reference Karpilovsky4, page 184]). Then
$\alpha $
-characters of G (see [Reference Karpilovsky4, page 184]). Then
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular if and only if
$\alpha $
-regular if and only if
![]() $\xi (x)\not = 0$
for some
$\xi (x)\not = 0$
for some
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
(see [Reference Karpilovsky5, Proposition 1.6.3]) and
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
(see [Reference Karpilovsky5, Proposition 1.6.3]) and
![]() $\vert \!\operatorname {\mathrm {Proj}}(G, \alpha )\vert $
is the number of
$\vert \!\operatorname {\mathrm {Proj}}(G, \alpha )\vert $
is the number of
![]() $\alpha $
-regular conjugacy classes of G (see [Reference Karpilovsky5, Theorem 1.3.6]).
$\alpha $
-regular conjugacy classes of G (see [Reference Karpilovsky5, Theorem 1.3.6]).
Let N be a normal subgroup of
![]() $G.$
Then G acts on
$G.$
Then G acts on
![]() $\operatorname {\mathrm {Proj}}(N, \alpha _N)$
by
$\operatorname {\mathrm {Proj}}(N, \alpha _N)$
by
for
![]() $\zeta \in \operatorname {\mathrm {Proj}}(N, \alpha _N), g\in G$
and all
$\zeta \in \operatorname {\mathrm {Proj}}(N, \alpha _N), g\in G$
and all
![]() $x\in N$
. Clifford’s theorem for projective characters applies to this action (see [Reference Karpilovsky5, Theorem 2.2.1]).
$x\in N$
. Clifford’s theorem for projective characters applies to this action (see [Reference Karpilovsky5, Theorem 2.2.1]).
A new concept of strict
![]() $\alpha ^d$
-regularity, which refines the notion of
$\alpha ^d$
-regularity, which refines the notion of
![]() $\alpha ^d$
-regularity, will be defined and investigated in Section 2 for d a divisor of the order of
$\alpha ^d$
-regularity, will be defined and investigated in Section 2 for d a divisor of the order of
![]() $[\alpha ].$
This concept will be used in Section 3 to give an alternative proof that the number of orbits of G under its action on
$[\alpha ].$
This concept will be used in Section 3 to give an alternative proof that the number of orbits of G under its action on
![]() $\operatorname {\mathrm {Proj}}(N, \alpha _N),$
for N a normal subgroup of
$\operatorname {\mathrm {Proj}}(N, \alpha _N),$
for N a normal subgroup of
![]() $G,$
is equal to the number of
$G,$
is equal to the number of
![]() $\alpha $
-regular conjugacy classes of G contained in N from [Reference Higgs2, Lemma 3.1]. It is also easy to show that this result is independent of the choice of
$\alpha $
-regular conjugacy classes of G contained in N from [Reference Higgs2, Lemma 3.1]. It is also easy to show that this result is independent of the choice of
![]() $2$
-cocycle from
$2$
-cocycle from
![]() $[\alpha ].$
The result is well known when
$[\alpha ].$
The result is well known when
![]() $\alpha $
is trivial (see [Reference Isaacs3, Corollary 6.33]); the method employed will be to apply this to the orbits of an
$\alpha $
is trivial (see [Reference Isaacs3, Corollary 6.33]); the method employed will be to apply this to the orbits of an
![]() $\alpha $
-covering group of G under its action on the irreducible characters and conjugacy classes of a normal subgroup, but to decompose these orbits into corresponding sets.
$\alpha $
-covering group of G under its action on the irreducible characters and conjugacy classes of a normal subgroup, but to decompose these orbits into corresponding sets.
2 Strictly
 $\alpha ^d$
-regular elements
$\alpha ^d$
-regular elements
Let
![]() $o(\phantom {.})$
denote the order of an element in a group. Then for
$o(\phantom {.})$
denote the order of an element in a group. Then for
![]() $[\beta ]\in M(G)$
, there exists
$[\beta ]\in M(G)$
, there exists
![]() $\alpha \in [\beta ]$
such that
$\alpha \in [\beta ]$
such that
![]() $o(\alpha ) = o([\beta ])$
and
$o(\alpha ) = o([\beta ])$
and
![]() $\alpha $
is a class-function cocycle, that is, the elements of
$\alpha $
is a class-function cocycle, that is, the elements of
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
are class functions (see [Reference Karpilovsky5, Corollary 4.1.6]). To avoid repetition throughout the rest of this paper, it will be assumed that
$\operatorname {\mathrm {Proj}}(G, \alpha )$
are class functions (see [Reference Karpilovsky5, Corollary 4.1.6]). To avoid repetition throughout the rest of this paper, it will be assumed that
![]() $\alpha $
has these two properties with
$\alpha $
has these two properties with
![]() $n = o(\alpha ).$
A consequence of the second property is that
$n = o(\alpha ).$
A consequence of the second property is that
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular if and only if
$\alpha $
-regular if and only if
![]() $f_{\alpha }(g, x) = 1$
for all
$f_{\alpha }(g, x) = 1$
for all
![]() $g\in G$
(see [Reference Karpilovsky5, page 33]). The first property allows us to make the following definition in terms of
$g\in G$
(see [Reference Karpilovsky5, page 33]). The first property allows us to make the following definition in terms of
![]() $\alpha ^d$
rather than for the more clumsy
$\alpha ^d$
rather than for the more clumsy
![]() $\beta \in [\alpha ]^d.$
$\beta \in [\alpha ]^d.$
Definition 2.1. Define
![]() $x\in G$
to be strictly
$x\in G$
to be strictly
![]() $\alpha ^d$
-regular if d is the smallest integer with
$\alpha ^d$
-regular if d is the smallest integer with
![]() $1\leq d\leq n$
such that x is
$1\leq d\leq n$
such that x is
![]() $\alpha ^d$
-regular.
$\alpha ^d$
-regular.
Next suppose
![]() $o(\alpha ^d)= o(\alpha ^k) = m.$
If
$o(\alpha ^d)= o(\alpha ^k) = m.$
If
![]() $\omega $
is a primitive mth root of unity, then there exists a field automorphism
$\omega $
is a primitive mth root of unity, then there exists a field automorphism
![]() $\tau $
of
$\tau $
of
![]() $\mathbb {Q}(\omega )$
over
$\mathbb {Q}(\omega )$
over
![]() $\mathbb Q$
such that
$\mathbb Q$
such that
![]() $\tau (\alpha ^d) =\alpha ^k.$
Consequently,
$\tau (\alpha ^d) =\alpha ^k.$
Consequently,
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha ^d$
-regular if and only if it is
$\alpha ^d$
-regular if and only if it is
![]() $\alpha ^k$
-regular. Thus,
$\alpha ^k$
-regular. Thus,
![]() $d\mid n$
in Definition 2.1.
$d\mid n$
in Definition 2.1.
Let
![]() $\pi (d)$
denote the set of prime numbers that divide d and let
$\pi (d)$
denote the set of prime numbers that divide d and let
![]() $d_p$
denote the pth part of d for any prime number
$d_p$
denote the pth part of d for any prime number
![]() $p.$
$p.$
Lemma 2.2. We have
![]() $x\in G$
is strictly
$x\in G$
is strictly
![]() $\alpha ^d$
-regular if and only if either:
$\alpha ^d$
-regular if and only if either:
-
(a) x is
 $\alpha ^d$
-regular but not
$\alpha ^d$
-regular but not
 $\alpha ^{d/p}$
-regular for each
$\alpha ^{d/p}$
-regular for each
 $p\in \pi (d);$
or
$p\in \pi (d);$
or -
(b)
 $o(\alpha _x) = d$
in
$o(\alpha _x) = d$
in
 $\operatorname {\mathrm {Lin}}(C_G(x)).$
$\operatorname {\mathrm {Lin}}(C_G(x)).$
Proof. For condition (a), if x is not
![]() $\alpha ^{d/p}$
-regular, then it is not
$\alpha ^{d/p}$
-regular, then it is not
![]() $\alpha ^t$
-regular for all positive integers t with
$\alpha ^t$
-regular for all positive integers t with
![]() $t\mid d/p.$
For condition (b), observe that x is
$t\mid d/p.$
For condition (b), observe that x is
![]() $\alpha ^d$
-regular if and only if
$\alpha ^d$
-regular if and only if
![]() $\alpha _x^d$
is trivial, that is,
$\alpha _x^d$
is trivial, that is,
![]() $o(\alpha _x)\mid d.$
Now for
$o(\alpha _x)\mid d.$
Now for
![]() $d> 1$
, x is strictly
$d> 1$
, x is strictly
![]() $\alpha ^d$
-regular if and only if
$\alpha ^d$
-regular if and only if
![]() $o(\alpha _x)\mid d$
, but
$o(\alpha _x)\mid d$
, but
![]() $\alpha _x^{d/p}\not =1$
for each prime
$\alpha _x^{d/p}\not =1$
for each prime
![]() $p\in \pi (d)$
from condition (a). The latter is true if and only if
$p\in \pi (d)$
from condition (a). The latter is true if and only if
![]() $d_p\mid o(\alpha _x)$
for each prime
$d_p\mid o(\alpha _x)$
for each prime
![]() $p\in \pi (d),$
that is, if and only if
$p\in \pi (d),$
that is, if and only if
![]() $d\mid o(\alpha _x).$
$d\mid o(\alpha _x).$
An equivalent way of stating Lemma 2.2(b) is that
![]() $x\in G$
is strictly
$x\in G$
is strictly
![]() $\alpha ^d$
-regular if and only if
$\alpha ^d$
-regular if and only if
![]() $\vert C_G(x)/C_{\alpha }(x)\vert = d.$
$\vert C_G(x)/C_{\alpha }(x)\vert = d.$
Now by definition for each
![]() $x\in G$
, there exists a unique
$x\in G$
, there exists a unique
![]() $d\mid n$
such that x is strictly
$d\mid n$
such that x is strictly
![]() $\alpha ^d$
-regular. Thus, the conjugacy classes of G are partitioned into strictly
$\alpha ^d$
-regular. Thus, the conjugacy classes of G are partitioned into strictly
![]() $\alpha ^d$
-regular conjugacy classes. So for
$\alpha ^d$
-regular conjugacy classes. So for
![]() $d\mid n$
and N a normal subgroup of
$d\mid n$
and N a normal subgroup of
![]() $G,$
let
$G,$
let
![]() $t_d$
be the number of strictly
$t_d$
be the number of strictly
![]() $\alpha ^d$
-regular conjugacy classes of G contained in
$\alpha ^d$
-regular conjugacy classes of G contained in
![]() $N.$
Thus, the number of
$N.$
Thus, the number of
![]() $\alpha ^d$
-regular conjugacy classes of G contained in N is
$\alpha ^d$
-regular conjugacy classes of G contained in N is
![]() $\sum _{s|d} t_s;$
in particular,
$\sum _{s|d} t_s;$
in particular,
![]() $\sum _{d\mid n} t_d = t(N),$
where
$\sum _{d\mid n} t_d = t(N),$
where
![]() $t(N)$
is the number of conjugacy classes of G contained in
$t(N)$
is the number of conjugacy classes of G contained in
![]() $N.$
$N.$
The choice of
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha $
allows the construction of an
$\alpha $
allows the construction of an
![]() $\alpha $
-covering group H of G with the following three properties (see [Reference Karpilovsky4, Section 4.1]):
$\alpha $
-covering group H of G with the following three properties (see [Reference Karpilovsky4, Section 4.1]):
-
(a) H has a cyclic subgroup
 $A\leq Z(H)\cap H'$
of order
$A\leq Z(H)\cap H'$
of order
 $n;$
$n;$
-
(b) there exists a conjugacy-preserving transversal (see below)
 $\{r(g): g\in G\}$
of A in H such that
$\{r(g): g\in G\}$
of A in H such that
 $\theta : H\rightarrow G$
defined by
$\theta : H\rightarrow G$
defined by
 $\theta (r(g)a) = g$
for all
$\theta (r(g)a) = g$
for all
 $g\in G$
and all
$g\in G$
and all
 $a\in A$
is a homomorphism with kernel
$a\in A$
is a homomorphism with kernel
 $A;$
$A;$
-
(c) there exists a faithful character
 $\lambda \in \operatorname {\mathrm {Lin}}(A)$
such that
$\lambda \in \operatorname {\mathrm {Lin}}(A)$
such that
 $\alpha (x, y) = \lambda (A(x, y))$
for all
$\alpha (x, y) = \lambda (A(x, y))$
for all
 $x, y\in G,$
where
$x, y\in G,$
where
 $r(x)r(y) = A(x, y)r(xy).$
$r(x)r(y) = A(x, y)r(xy).$
A conjugacy-preserving transversal means that
![]() $r(x)$
and
$r(x)$
and
![]() $r(y)$
are conjugate in H if and only if x and y are conjugate in G (see [Reference Karpilovsky5, Lemma 4.1.1]).
$r(y)$
are conjugate in H if and only if x and y are conjugate in G (see [Reference Karpilovsky5, Lemma 4.1.1]).
It is easy to see that
![]() $\theta (C_H(r(x))) = C_{\alpha }(x)$
for
$\theta (C_H(r(x))) = C_{\alpha }(x)$
for
![]() $x\in G$
and
$x\in G$
and
![]() $\theta (C_H(r(x)A)) = C_G(x).$
Thus, working in H, we see that x is strictly
$\theta (C_H(r(x)A)) = C_G(x).$
Thus, working in H, we see that x is strictly
![]() $\alpha ^d$
-regular if and only if the cyclic group
$\alpha ^d$
-regular if and only if the cyclic group
![]() $C_H(r(x)A)/C_H(r(x))$
has order
$C_H(r(x)A)/C_H(r(x))$
has order
![]() $d.$
$d.$
Proposition 2.3. Let H be an
![]() $\alpha $
-covering group of
$\alpha $
-covering group of
![]() $G.$
Then
$G.$
Then
![]() $x\in G$
is strictly
$x\in G$
is strictly
![]() $\alpha ^d$
-regular if and only if either:
$\alpha ^d$
-regular if and only if either:
-
(a)
 $r(x)\langle z^m\rangle $
are the conjugates of
$r(x)\langle z^m\rangle $
are the conjugates of
 $r(x)$
in
$r(x)$
in
 $r(x)A,$
where
$r(x)A,$
where
 $\langle z\rangle = A$
and
$\langle z\rangle = A$
and
 $dm = n$
; or
$dm = n$
; or -
(b)
 $\{r(x)z^i: i = 1,\ldots , m\}$
is a maximal set of conjugacy class representatives of H in
$\{r(x)z^i: i = 1,\ldots , m\}$
is a maximal set of conjugacy class representatives of H in
 $r(x)A.$
$r(x)A.$
Proof. Define
![]() $k_{r(x)} : C_H(r(x)A)\rightarrow A$
by
$k_{r(x)} : C_H(r(x)A)\rightarrow A$
by
![]() $k_{r(x)}(h) = hr(x)h^{-1}(r(x))^{-1}.$
Then
$k_{r(x)}(h) = hr(x)h^{-1}(r(x))^{-1}.$
Then
![]() $k_{r(x)}$
is a homomorphism with kernel
$k_{r(x)}$
is a homomorphism with kernel
![]() $C_H(r(x))$
, since
$C_H(r(x))$
, since
![]() $\lambda (k_{r(x)}) = \alpha _x.$
Now let z be a generator of A. Then
$\lambda (k_{r(x)}) = \alpha _x.$
Now let z be a generator of A. Then
![]() $r(x)z^i$
and
$r(x)z^i$
and
![]() $r(x)z^j$
are conjugate if and only if
$r(x)z^j$
are conjugate if and only if
![]() $z^{j-i}\in \operatorname {\mathrm {Im}}(k_{r(x)}),$
that is, if and only if
$z^{j-i}\in \operatorname {\mathrm {Im}}(k_{r(x)}),$
that is, if and only if
![]() $z^i\operatorname {\mathrm {Im}}(k_{r(x)}) = z^j\operatorname {\mathrm {Im}}(k_{r(x)}).$
$z^i\operatorname {\mathrm {Im}}(k_{r(x)}) = z^j\operatorname {\mathrm {Im}}(k_{r(x)}).$
Now x is strictly
![]() $\alpha ^d$
-regular if and only if
$\alpha ^d$
-regular if and only if
![]() $\operatorname {\mathrm {Im}}(k_{r(x)}) = \langle z^m\rangle ,$
that is, if and only if the cosets of
$\operatorname {\mathrm {Im}}(k_{r(x)}) = \langle z^m\rangle ,$
that is, if and only if the cosets of
![]() $\operatorname {\mathrm {Im}}(k_{r(x)})$
in A are
$\operatorname {\mathrm {Im}}(k_{r(x)})$
in A are
![]() $z^i\langle z^m\rangle $
for
$z^i\langle z^m\rangle $
for
![]() $i =1,\ldots , m.$
$i =1,\ldots , m.$
3 Counting orbits of projective characters
Let N be a subgroup of
![]() $G.$
Let H be an
$G.$
Let H be an
![]() $\alpha $
-covering group of G and, using the notation of Section 2, let M be the subgroup of H containing A such that
$\alpha $
-covering group of G and, using the notation of Section 2, let M be the subgroup of H containing A such that
![]() $\theta (M) = N.$
Finally, for any integer k, let
$\theta (M) = N.$
Finally, for any integer k, let
![]() $\operatorname {\mathrm {Irr}}(M\vert \lambda ^k) = \{\chi \in \operatorname {\mathrm {Irr}}(M): \chi _A = \chi (1)\lambda ^k\},$
where
$\operatorname {\mathrm {Irr}}(M\vert \lambda ^k) = \{\chi \in \operatorname {\mathrm {Irr}}(M): \chi _A = \chi (1)\lambda ^k\},$
where
![]() $\operatorname {\mathrm {Irr}}(M)$
is the set of irreducible characters of
$\operatorname {\mathrm {Irr}}(M)$
is the set of irreducible characters of
![]() $M.$
Then the mapping from
$M.$
Then the mapping from
![]() $\operatorname {\mathrm {Proj}}(N, \alpha _N^k)$
to
$\operatorname {\mathrm {Proj}}(N, \alpha _N^k)$
to
![]() $\operatorname {\mathrm {Irr}}(M\vert \lambda ^k), \zeta \mapsto \chi $
is a bijection, where
$\operatorname {\mathrm {Irr}}(M\vert \lambda ^k), \zeta \mapsto \chi $
is a bijection, where
![]() $\zeta (x) = \chi (r(x))$
for all
$\zeta (x) = \chi (r(x))$
for all
![]() $x\in N$
(see [Reference Karpilovsky4, pages 134–135] or [Reference Karpilovsky5, Corollary 4.1.3]). Now suppose N is normal in G, then it is easy to check that
$x\in N$
(see [Reference Karpilovsky4, pages 134–135] or [Reference Karpilovsky5, Corollary 4.1.3]). Now suppose N is normal in G, then it is easy to check that
![]() $\zeta ^g = \chi ^{r(g)}$
for all
$\zeta ^g = \chi ^{r(g)}$
for all
![]() $g\in G$
and hence the orbit length of
$g\in G$
and hence the orbit length of
![]() $\zeta $
under the action of G equals that of
$\zeta $
under the action of G equals that of
![]() $\chi $
under the action of
$\chi $
under the action of
![]() $H.$
By definition, for each
$H.$
By definition, for each
![]() $x\in G$
, there exists a unique
$x\in G$
, there exists a unique
![]() $d\mid n$
such that x is strictly
$d\mid n$
such that x is strictly
![]() $\alpha ^d$
-regular. Thus, the conjugacy classes of H are partitioned according to
$\alpha ^d$
-regular. Thus, the conjugacy classes of H are partitioned according to
![]() $\vert C_H(r(x)A)/C_H(r(x)\vert $
for
$\vert C_H(r(x)A)/C_H(r(x)\vert $
for
![]() $r(x)a,$
where
$r(x)a,$
where
![]() $x\in G$
and
$x\in G$
and
![]() $a\in A.$
However, if x is a strictly
$a\in A.$
However, if x is a strictly
![]() $\alpha ^d$
-regular conjugacy class representative of
$\alpha ^d$
-regular conjugacy class representative of
![]() $G,$
then
$G,$
then
![]() $n/d$
corresponding conjugacy class representatives of H are obtained as detailed in Proposition 2.3. So the number of conjugacy classes of H in M corresponding to the number of
$n/d$
corresponding conjugacy class representatives of H are obtained as detailed in Proposition 2.3. So the number of conjugacy classes of H in M corresponding to the number of
![]() $\alpha ^d$
-regular conjugacy classes of G contained in N is
$\alpha ^d$
-regular conjugacy classes of G contained in N is
![]() $\sum _{s|d} (n/s)t_s;$
in particular,
$\sum _{s|d} (n/s)t_s;$
in particular,
![]() $\sum _{d|n} (n/d)t_d = t(M),$
where
$\sum _{d|n} (n/d)t_d = t(M),$
where
![]() $t(M)$
is the number of conjugacy classes of H contained in
$t(M)$
is the number of conjugacy classes of H contained in
![]() $M.$
$M.$
Lemma 3.1. Let N be a normal subgroup of G and suppose that
![]() $o(\alpha ^d) = o(\alpha ^k).$
Let
$o(\alpha ^d) = o(\alpha ^k).$
Let
![]() $\sigma $
be a field automorphism of
$\sigma $
be a field automorphism of
![]() $\mathbb {C}$
that extends
$\mathbb {C}$
that extends
![]() $\tau $
, as described in Section 2, so that
$\tau $
, as described in Section 2, so that
![]() $\sigma (\alpha ^d) = \alpha ^k.$
Then
$\sigma (\alpha ^d) = \alpha ^k.$
Then
![]() $\zeta ^g = \zeta '$
if and only if
$\zeta ^g = \zeta '$
if and only if
![]() $\sigma (\zeta )^{g} = \sigma (\zeta ')$
for
$\sigma (\zeta )^{g} = \sigma (\zeta ')$
for
![]() $g\in G$
and
$g\in G$
and
![]() $\zeta \in \operatorname {\mathrm {Proj}}(N, \alpha _N^d).$
$\zeta \in \operatorname {\mathrm {Proj}}(N, \alpha _N^d).$
Proof. If
![]() $\zeta \in \operatorname {\mathrm {Proj}}(N, \alpha _N^d),$
then
$\zeta \in \operatorname {\mathrm {Proj}}(N, \alpha _N^d),$
then
![]() $\sigma (\zeta )\in \operatorname {\mathrm {Proj}}(N, \sigma (\alpha _N^d)).$
Now
$\sigma (\zeta )\in \operatorname {\mathrm {Proj}}(N, \sigma (\alpha _N^d)).$
Now
for all
![]() $x\in N.$
$x\in N.$
Lemma 3.1 sets up a one-to-one correspondence between the orbits of G under its action on
![]() $\operatorname {\mathrm {Proj}}(N, \alpha _N^d)$
and those under its action on
$\operatorname {\mathrm {Proj}}(N, \alpha _N^d)$
and those under its action on
![]() $\operatorname {\mathrm {Proj}}(N, \alpha _N^k)$
in which orbit lengths are preserved. We next just restate Lemma 3.1 for an
$\operatorname {\mathrm {Proj}}(N, \alpha _N^k)$
in which orbit lengths are preserved. We next just restate Lemma 3.1 for an
![]() $\alpha $
-covering group H of
$\alpha $
-covering group H of
![]() $G.$
$G.$
Corollary 3.2. Suppose that
![]() $o(\lambda ^d) = o(\lambda ^k)$
in
$o(\lambda ^d) = o(\lambda ^k)$
in
![]() $\langle \lambda \rangle = \operatorname {\mathrm {Lin}}(A).$
Let
$\langle \lambda \rangle = \operatorname {\mathrm {Lin}}(A).$
Let
![]() $\sigma $
be as in Lemma 3.1, so that
$\sigma $
be as in Lemma 3.1, so that
![]() $\sigma (\lambda ^d)=\lambda ^k.$
Then
$\sigma (\lambda ^d)=\lambda ^k.$
Then
![]() $\chi ^h = \chi '$
if and only if
$\chi ^h = \chi '$
if and only if
![]() $\sigma (\chi )^h = \sigma (\chi ')$
for
$\sigma (\chi )^h = \sigma (\chi ')$
for
![]() $h\in H$
and
$h\in H$
and
![]() $\chi \in \operatorname {\mathrm {Irr}}(M\vert \lambda ^d).$
$\chi \in \operatorname {\mathrm {Irr}}(M\vert \lambda ^d).$
Let
![]() $\phi $
denote Euler’s totient function. We use the well-known result from number theory that
$\phi $
denote Euler’s totient function. We use the well-known result from number theory that
![]() $\sum _{d\mid n}\phi (d) = \sum _{d\mid n}\phi (n/d) = n.$
$\sum _{d\mid n}\phi (d) = \sum _{d\mid n}\phi (n/d) = n.$
Theorem 3.3. Let N be a normal subgroup of
![]() $G.$
Then the number of orbits of G under its action on
$G.$
Then the number of orbits of G under its action on
![]() $\operatorname {\mathrm {Proj}}(N, \alpha _N)$
is equal to the number of
$\operatorname {\mathrm {Proj}}(N, \alpha _N)$
is equal to the number of
![]() $\alpha $
-regular conjugacy classes of G contained in
$\alpha $
-regular conjugacy classes of G contained in
![]() $N.$
$N.$
Proof. Proceeding by induction, we count the number of
![]() $\alpha ^d$
-regular conjugacy classes of G contained in N. First, if
$\alpha ^d$
-regular conjugacy classes of G contained in N. First, if
![]() $d = n,$
then, as previously stated, the number of conjugacy classes of G contained in N is equal to the number of orbits of G under its action on
$d = n,$
then, as previously stated, the number of conjugacy classes of G contained in N is equal to the number of orbits of G under its action on
![]() $\operatorname {\mathrm {Irr}}(N).$
So assume by induction that the number of orbits of G under its action on
$\operatorname {\mathrm {Irr}}(N).$
So assume by induction that the number of orbits of G under its action on
![]() $\operatorname {\mathrm {Proj}}(N, \alpha _N^d)$
is equal to the number of
$\operatorname {\mathrm {Proj}}(N, \alpha _N^d)$
is equal to the number of
![]() $\alpha ^d$
-regular conjugacy classes of G contained in N for each
$\alpha ^d$
-regular conjugacy classes of G contained in N for each
![]() $d\mid n$
with
$d\mid n$
with
![]() $d\not = 1.$
Let H be an
$d\not = 1.$
Let H be an
![]() $\alpha $
-covering group of G and let M denote the subgroup of H containing A such that
$\alpha $
-covering group of G and let M denote the subgroup of H containing A such that
![]() $\theta (M) = N.$
$\theta (M) = N.$
Now for
![]() $d\mid n$
and
$d\mid n$
and
![]() $d\not = 1$
, G has
$d\not = 1$
, G has
![]() $\sum _{s\mid d} t_s$
orbits under its action on
$\sum _{s\mid d} t_s$
orbits under its action on
![]() $\operatorname {\mathrm {Proj}}(N, \alpha _N^d).$
Thus, H has the same number of orbits under its action on
$\operatorname {\mathrm {Proj}}(N, \alpha _N^d).$
Thus, H has the same number of orbits under its action on
![]() $\operatorname {\mathrm {Irr}}(M\vert \lambda ^d).$
Now
$\operatorname {\mathrm {Irr}}(M\vert \lambda ^d).$
Now
![]() $o(\lambda ^k) = o(\lambda ^d)$
for
$o(\lambda ^k) = o(\lambda ^d)$
for
![]() $\phi (n/d)$
values of k with
$\phi (n/d)$
values of k with
![]() $1\leq k\leq n.$
Thus, using Corollary 3.2, the total number of orbits of H under its actions on
$1\leq k\leq n.$
Thus, using Corollary 3.2, the total number of orbits of H under its actions on
![]() $\operatorname {\mathrm {Irr}}(M\vert \lambda ^c),$
for the
$\operatorname {\mathrm {Irr}}(M\vert \lambda ^c),$
for the
![]() $n - \phi (n)$
values of c with
$n - \phi (n)$
values of c with
![]() $1\leq c\leq n$
that are not relatively prime to
$1\leq c\leq n$
that are not relatively prime to
![]() $n,$
is
$n,$
is
 $$ \begin{align*} \sum_{\substack{d\mid n\\ d\not=1}}\phi\bigg(\frac{n}{d}\bigg)\bigg(\sum_{s\mid d} t_s\bigg) &= \sum_{s\mid d} t_s\bigg(\sum_{\substack{d\mid n\\ d\not=1}}\phi\bigg(\frac{n}{d}\bigg)\bigg) \\ &= \sum_{s\mid n} t_s\bigg(\sum_{\substack{r\mid (n/s)\\ (r, s)\not=(1,1)}}\phi\bigg(\frac{n/s}{r}\bigg)\bigg) \\ &= t_1(n-\phi(n))+ \sum_{\substack{s\mid n\\ s\not=1}}t_s\frac{n}{s}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{d\mid n\\ d\not=1}}\phi\bigg(\frac{n}{d}\bigg)\bigg(\sum_{s\mid d} t_s\bigg) &= \sum_{s\mid d} t_s\bigg(\sum_{\substack{d\mid n\\ d\not=1}}\phi\bigg(\frac{n}{d}\bigg)\bigg) \\ &= \sum_{s\mid n} t_s\bigg(\sum_{\substack{r\mid (n/s)\\ (r, s)\not=(1,1)}}\phi\bigg(\frac{n/s}{r}\bigg)\bigg) \\ &= t_1(n-\phi(n))+ \sum_{\substack{s\mid n\\ s\not=1}}t_s\frac{n}{s}. \end{align*} $$
The total number of orbits of H under its action on
![]() $\operatorname {\mathrm {Irr}}(M)$
is
$\operatorname {\mathrm {Irr}}(M)$
is
![]() $t(M),$
so the total number of orbits of H under its actions on
$t(M),$
so the total number of orbits of H under its actions on
![]() $\operatorname {\mathrm {Irr}}(M\vert \lambda ^c),$
for the
$\operatorname {\mathrm {Irr}}(M\vert \lambda ^c),$
for the
![]() $\phi (n)$
values of c with
$\phi (n)$
values of c with
![]() $1\leq c\leq n$
that are relatively prime to
$1\leq c\leq n$
that are relatively prime to
![]() $n,$
is
$n,$
is
 $$ \begin{align*}t(M) - t_1(n-\phi(n)) - \sum_{\substack{s\mid n\\ s\not=1}} t_s\frac{n}{s} = t_1\phi(n).\end{align*} $$
$$ \begin{align*}t(M) - t_1(n-\phi(n)) - \sum_{\substack{s\mid n\\ s\not=1}} t_s\frac{n}{s} = t_1\phi(n).\end{align*} $$
Hence, the number of orbits of H under its action on
![]() $\operatorname {\mathrm {Irr}}(M\vert \lambda )$
(and the number of orbits of G under its action on
$\operatorname {\mathrm {Irr}}(M\vert \lambda )$
(and the number of orbits of G under its action on
![]() $\operatorname {\mathrm {Proj}}(N, \alpha _N)$
) is
$\operatorname {\mathrm {Proj}}(N, \alpha _N)$
) is
![]() $t_1,$
as required.
$t_1,$
as required.
Suppose that
![]() $\beta = t(\delta )\alpha .$
Then from [Reference Higgs1, Lemma 1.4], we see that
$\beta = t(\delta )\alpha .$
Then from [Reference Higgs1, Lemma 1.4], we see that
![]() $\operatorname {\mathrm {Proj}}(N, \beta _N) = \{\delta _N\zeta : \zeta \in \operatorname {\mathrm {Proj}}(N, \alpha _N)\}$
and, for
$\operatorname {\mathrm {Proj}}(N, \beta _N) = \{\delta _N\zeta : \zeta \in \operatorname {\mathrm {Proj}}(N, \alpha _N)\}$
and, for
![]() $g\in G$
,
$g\in G$
,
![]() $\zeta ^g = \zeta '$
if and only if
$\zeta ^g = \zeta '$
if and only if
![]() $(\delta _N\zeta )^g = \delta _N\zeta '$
for
$(\delta _N\zeta )^g = \delta _N\zeta '$
for
![]() $\zeta \in \operatorname {\mathrm {Proj}}(N, \alpha _N).$
In particular, this establishes a one-to-one correspondence between the orbits of G under its action on
$\zeta \in \operatorname {\mathrm {Proj}}(N, \alpha _N).$
In particular, this establishes a one-to-one correspondence between the orbits of G under its action on
![]() $\operatorname {\mathrm {Proj}}(N, \beta _N)$
and those under its action on
$\operatorname {\mathrm {Proj}}(N, \beta _N)$
and those under its action on
![]() $\operatorname {\mathrm {Proj}}(N, \alpha _N)$
in which orbit lengths are preserved. So from this and Lemma 3.1, the result of Theorem 3.3 is independent of the choice of
$\operatorname {\mathrm {Proj}}(N, \alpha _N)$
in which orbit lengths are preserved. So from this and Lemma 3.1, the result of Theorem 3.3 is independent of the choice of
![]() $2$
-cocycle from
$2$
-cocycle from
![]() $[\alpha ]^c$
for c relatively prime to
$[\alpha ]^c$
for c relatively prime to
![]() $n.$
$n.$